 集合と位相
集合と位相 局所コンパクトの定義と性質とその証明
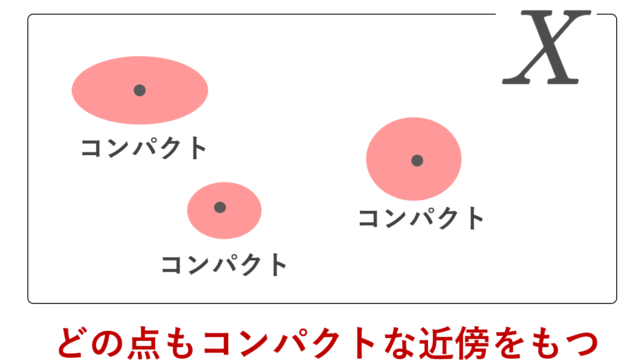
位相空間における局所コンパクト空間とは,各点がコンパクトな近傍を持つ空間のことを言います。ただし,文献によって定義が異なることがあるため,注意が必要です。本記事では,局所コンパクトの,さまざまな流儀の定義を紹介し,その定義がハウスドルフ空間のときは同値になることや,その他局所コンパクト空間・局所コンパクトハウスドルフ空間の性質を証明付きで解説します。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  本・サイトの紹介
本・サイトの紹介  集合と位相
集合と位相