 微分積分学(大学)
微分積分学(大学) ガウス積分のさまざまな形とその証明5つ
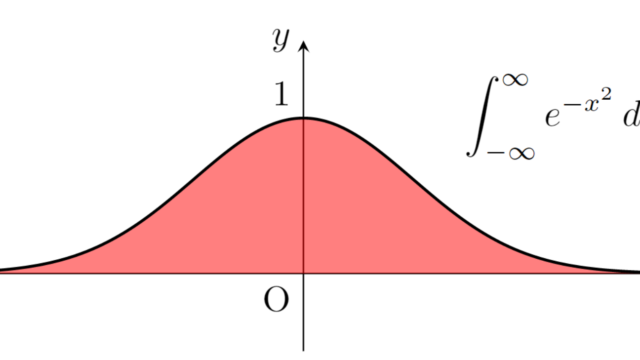
ガウス関数e^-x^2の積分であるガウス積分 (Gaussian integral) について,そのさまざまな形を紹介し,5通りの証明を紹介します。証明は,極座標変換・直交座標変換・ガンマ関数・ウォリス積分・回転体の体積を用いたものを順に紹介します。
 微分積分学(大学)
微分積分学(大学) 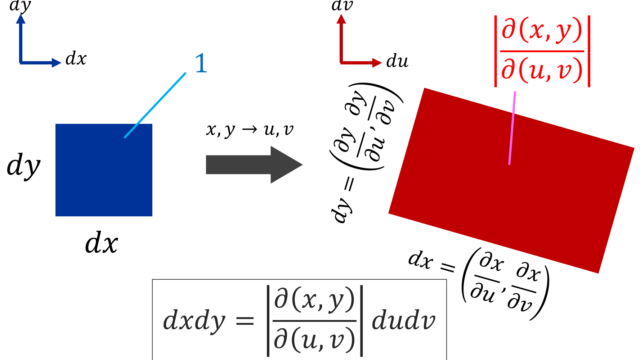 微分積分学(大学)
微分積分学(大学) 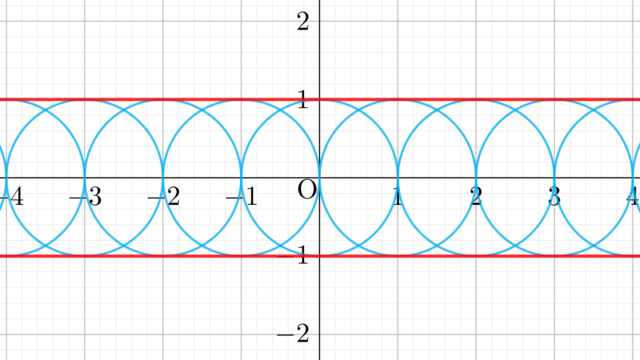 微分積分学(大学)
微分積分学(大学) 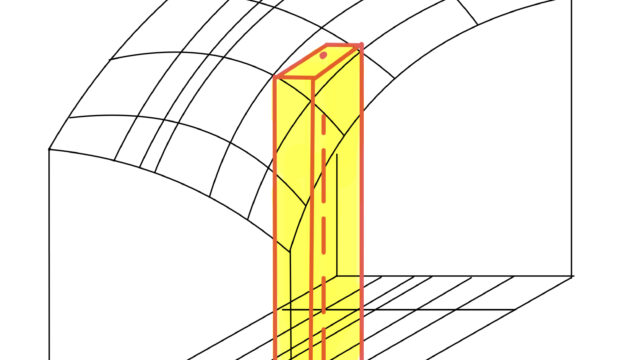 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)