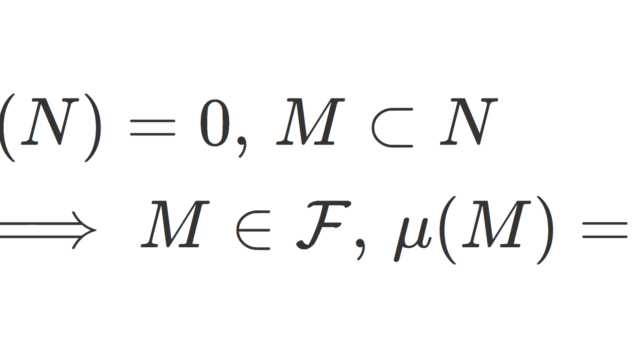 測度論
測度論 完備な測度と測度空間の完備化
完備な測度空間とは,零集合の任意の部分集合が可測,従って零集合になる測度空間のことをいいます。任意の測度空間は完備な拡張を持つことが知られています。完備な測度と,任意の測度空間の完備化について紹介しましょう。
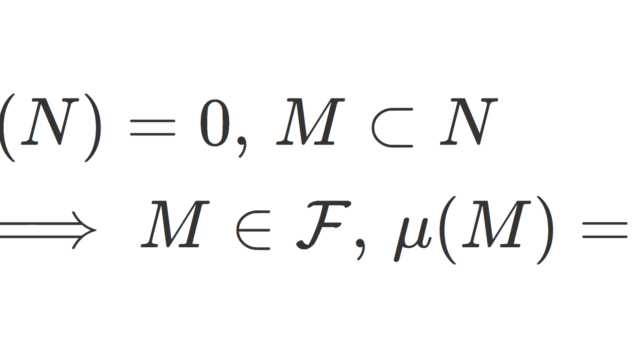 測度論
測度論  測度論
測度論  測度論
測度論 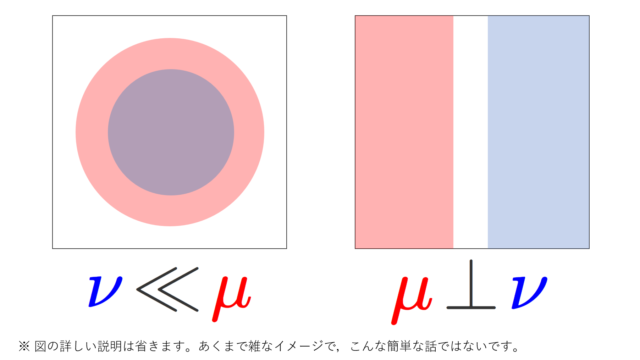 測度論
測度論 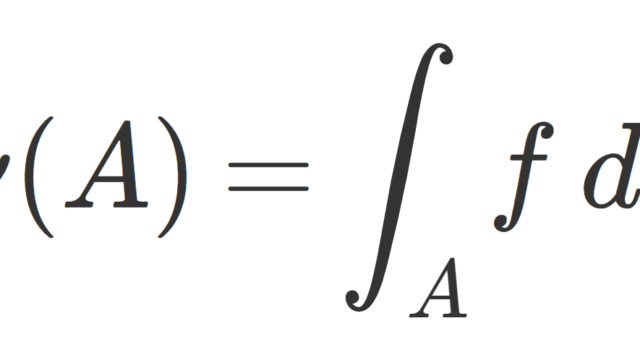 測度論
測度論 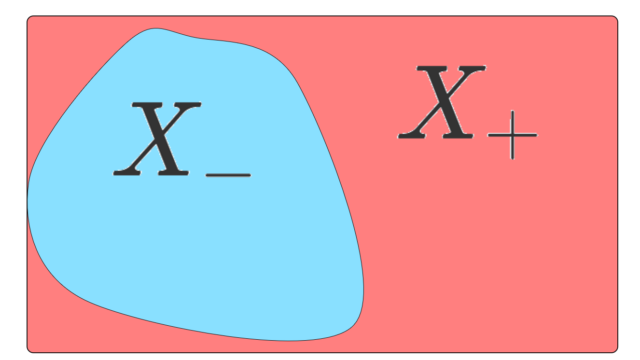 測度論
測度論 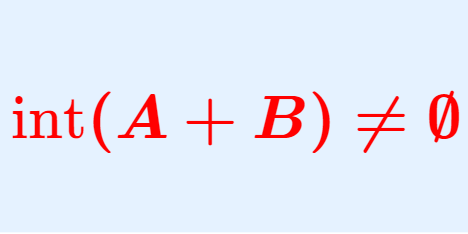 測度論
測度論  測度論
測度論  測度論
測度論  測度論
測度論