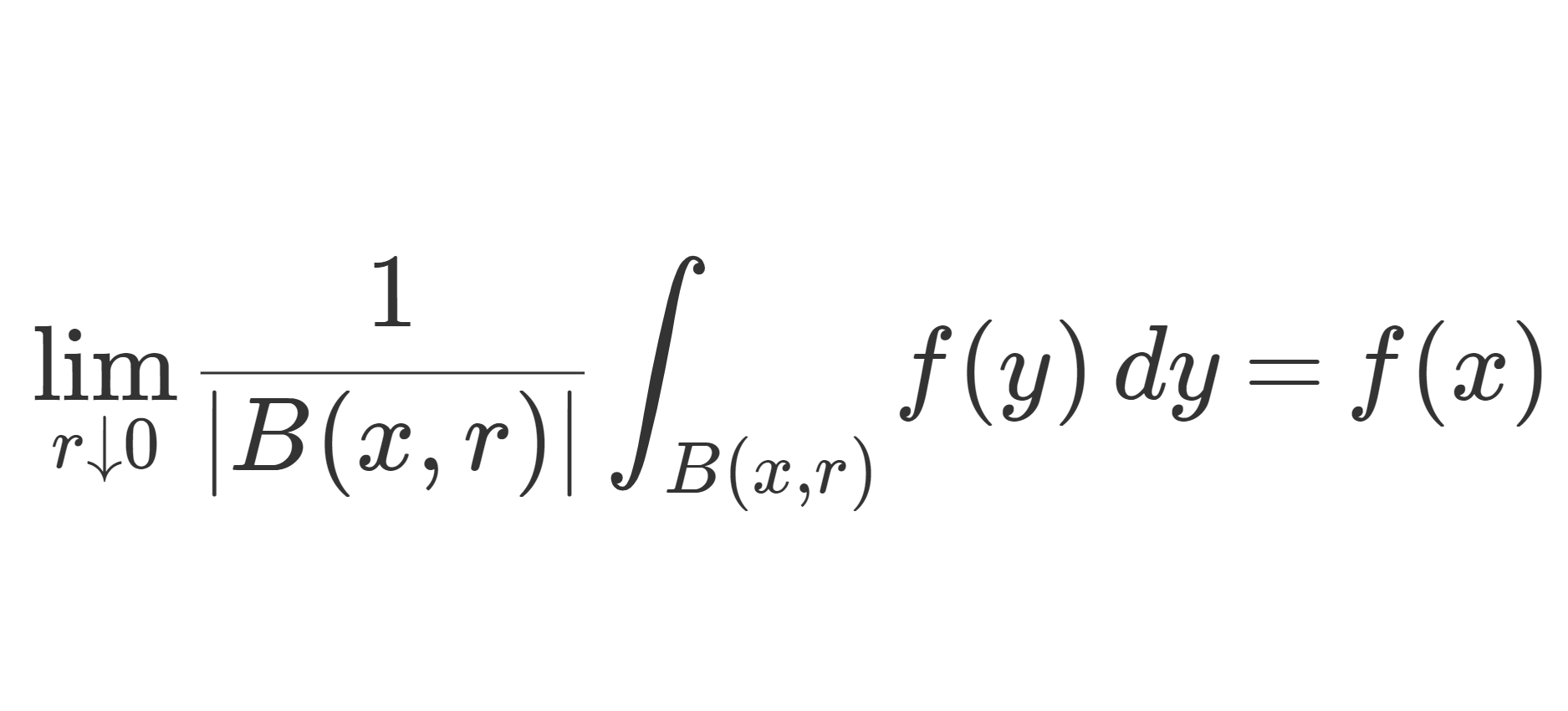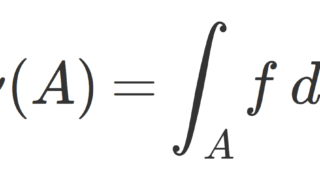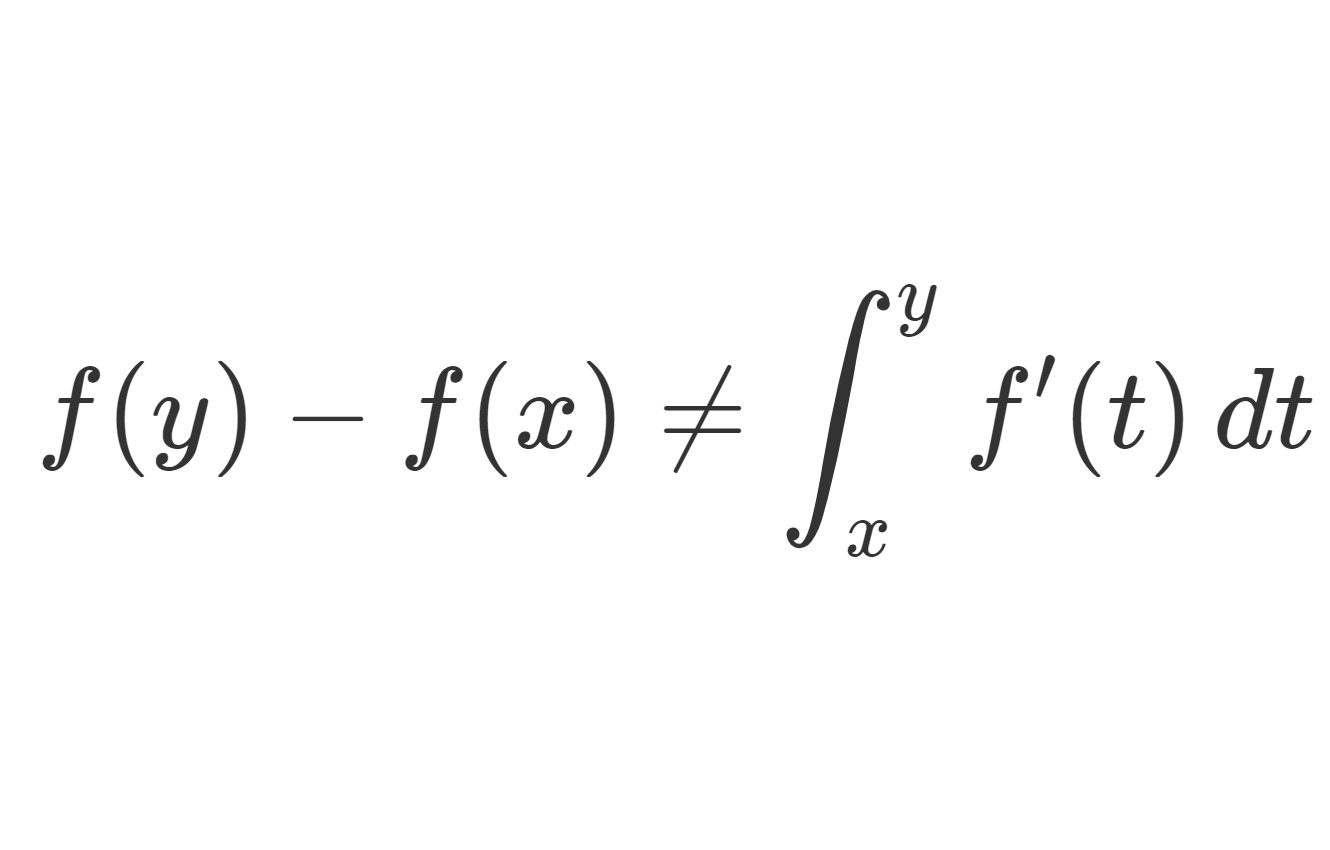ルベーグの微分定理は,リーマン積分のときに成り立っていた「積分して微分すると元に戻る」という性質の,ルベーグ積分版といえます。
ルベーグの微分定理とその証明を行い,測度の微分について少し掘り下げましょう。
ルベーグの微分定理
ルベーグの微分定理 (Lebesgue differentiation theorem)
f\colon \R^n \to \mathbb{C} を可積分関数( \int_{\R^n} |f|\, dx<\infty をみたす関数)とする。 B(x,r)=\{ y\in \R^n \mid |y-x|<r\} を x 中心,半径 r の開球とする。
このとき,ほとんどいたる x\in \R^n に対し,
\color{red}\lim_{r\downarrow 0 } \frac{1}{|B(x,r)|}\int_{B(x,r)}|f(y)-f(x)|\, dy =0
が成り立つ。ただし,{|B(x,r)|} は B(x,r) のルベーグ測度を指す。 特に,ほとんどいたる x\in \R^n に対し,微分公式
が成り立つ。
赤字の式が成り立つような x\in \R^n をルベーグ点 (Lebesgue point) ということがあります。「特に」以下は,
\begin{aligned}&\left|\frac{1}{|B(x,r)|}\int_{B(x,r)}f(y)\, dy -f(x)\right| \\ &= \left|\frac{1}{|B(x,r)|}\int_{B(x,r)}\{f(y)-f(x)\}\, dy\right| \\ &\le \frac{1}{|B(x,r)|}\int_{B(x,r)}|f(y)-f(x)|\, dy \end{aligned}
と赤字の式+はさみうちの原理から分かります。
もし f が連続関数であれば,これは単なる微分積分学の基本定理 (Fundamental Theorem of Calculus) で,当たり前に成り立つものです。今回は,単なる可積分関数でもほとんどいたるところで成り立つというのが重要です。
n=1 すなわち1次元のとき, B(x,r)=(x-r, x+r) であり,定理中の赤字の式は
\lim_{r\downarrow 0 } \frac{1}{2r}\int_{x-r}^{x+r} |f(y)-f(x)|\, dx =0
となります。実際のところは,より一般に以下が成立します。
ルベーグの微分定理の1次元版
f\colon \R \to \mathbb{C} を可積分関数とする。このとき,ほとんどいたる x\in \R^n において,
\color{red}\lim_{h\to 0 } \frac{1}{h}\int_{x}^{x+h}|f(y)-f(x)|\, dy =0
が成り立つ。特に,ほとんどいたる x\in \R^n において,微分公式
が成り立つ。
ルベーグの微分定理の1次元版は,ルベーグの微分定理を認めると簡単に示せます。実際,
\begin{aligned} &\frac{1}{h}\int_{x}^{x+h}|f(y)-f(x)|\, dy \\ &\le 2\cdot \frac{1}{2h} \int_{x-h}^{x+h}|f(y)-f(x)|\, dy \end{aligned}
とはさみうちの原理でスグ分かります。
ルベーグの微分定理の証明
かなり長くなってしまいましたが,少しずつ理解していきましょう。
以下で, \|f\|_1 =\int_{\R^n} |f|\, dx とします。
証明
x\in \R^n,\, r>0 と可積分関数 f に対し,
T_rf(x)=\frac{1}{|B(x,r)|}\int_{B(x,r)} |f(y)-f(x)|\, dy
とし,\displaystyle Tf(x)=\limsup_{r\downarrow 0} T_rf(x) としたとき,示すべきは Tf(x)=0,\; \text{a.e.}\, x\in \R^n である。
\varepsilon>0 とする。コンパクト台をもつ連続関数の空間 C_c(\R^n)\subset L^1(\R^n) は L^1(\R^n) において稠密であるから, \|f-g_\varepsilon\|_1 <\varepsilon となる g_\varepsilon\in C_c(\R^n) が取れる。 g_\varepsilon は連続なので, Tg_\varepsilon=0 である。 h_\varepsilon=f-g_\varepsilon とおく。
\begin{aligned} &T_rh_\varepsilon(x)\\ &\le \frac{1}{|B(x,r)|}\int_{B(x,r)} |h_\varepsilon(y)|\, dy +|h_\varepsilon(x)|\end{aligned}
より,
と定めると, Th_\varepsilon\le Mh_\varepsilon+|h_\varepsilon| である。さらに T_rf\le T_rg_\varepsilon+T_rh_\varepsilon,\; Tg_\varepsilon=0 なので,
となる。\lambda>0 とすると,
である。ただし, \{Tf>2\lambda\}=\{ x\in\R^n \mid Tf(x)>2\lambda\} の意味で,他も同様である。マルコフの不等式より,
である(左辺はルベーグ測度)。ここで, |\{ Mh_\varepsilon>\lambda\}| \le 3^n \varepsilon/\lambda を示せたとする(後で示す)。このとき,
となるが,左辺は \varepsilon に依らないため, \varepsilon\downarrow 0 として, |\{ Tf>2\lambda\}|=0 となる。結局 |\{Tf>0\}|=0 なので, Tf=0,\; \text{a.e.} が示された。
途中で用いた |\{ Mh_\varepsilon>\lambda\}| \le 3^n \varepsilon/\lambda を示す。
より一般に,\displaystyle Mf(x)=\sup_{0<r<\infty}\frac{1}{|B(x,r)|}\int_{B(x,r)} |f(y)| \, dy に対し,
\color{red} |\{ Mf>\lambda\}| \le 3^n \|f\|_1 /\lambda
を示せばよい。 K\subset \{ Mf >\lambda\} をコンパクト集合とする。各 x\in K に対して,ある r_x>0 が存在して,
すなわち,
とできる。 K はコンパクトなので, K\subset \bigcup_{i=1}^t B(x_i, r_{x_i}) となる x_1,x_2,\dots, x_t\in K,\; r_{x_1} \ge r_{x_2}\ge \dots \ge r_{x_t}>0 が存在する。 B_i=B(x_i, r_{x_i}) と略記する。 \{B_i\} から部分列 \{C_j\} を次のように作る:
まず C_1= B_1 とし,次に C_2 は C_1 と交わらない最小の番号の B_i とする。 C_3 は C_1\cup C_2 と交わらない最小の番号の B_{i'}\;(i'>i) とする。これを続けて,できるだけ多くの集合 B_i を部分列 \{C_j\} としてとる。
このとき, \{C_j\} はどの二つも共通部分をもたない。 C_j = B(y_j, s_j) とする。 B(x,r) と共通部分をもつ B(y, r') \; (r'\le r) は,下の図のように, B(x, 3r) に含まれる。これを踏まえると,
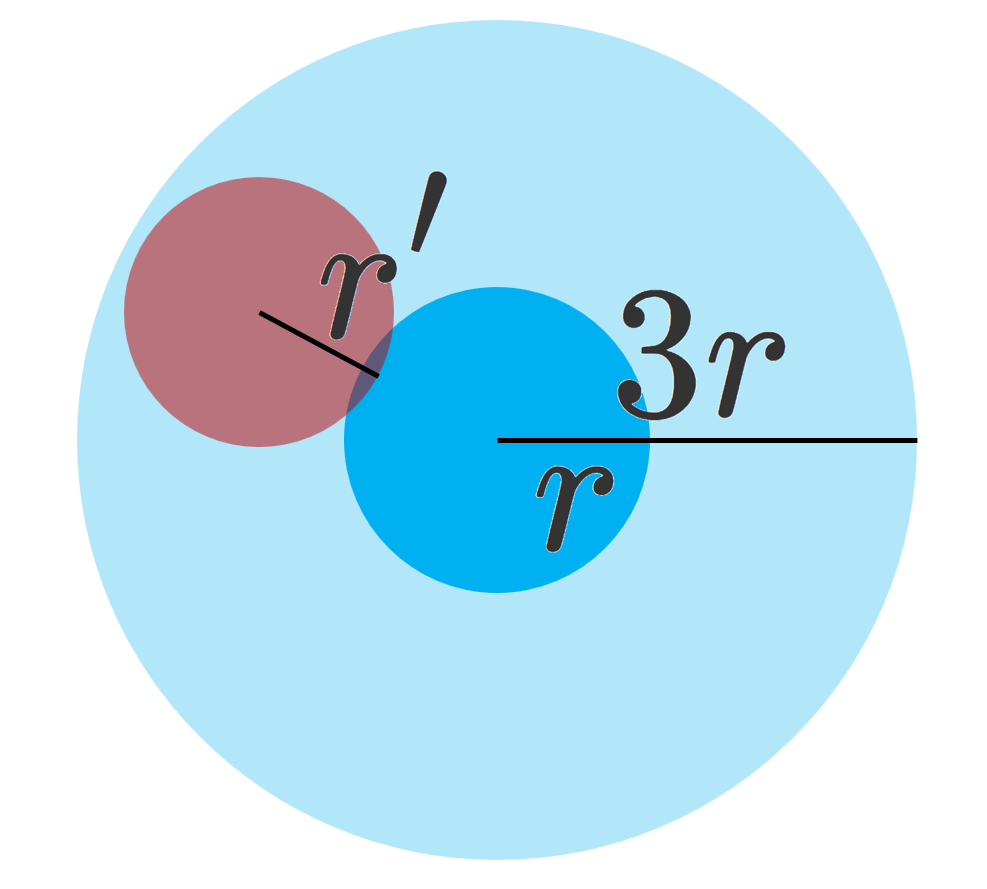
である。したがって |K| \le \sum_j |B(y_j, 3s_j)| = 3^n \sum_j |C_j| である。さらに,
であるから,結局 |K|\le 3^n \|f\|_1/\lambda である。ルベーグ測度の内部正則性より, |\{ Mf>\lambda\}| \le 3^n \|f\|_1 /\lambda が示された。
証明終
なお,ここで出てくる関数
Mf(x)=\sup_{0<r<\infty}\frac{1}{|B(x,r)|}\int_{B(x,r)} |f(y)| \, dy
をハーディ-リトルウッドの極大函数 (Hardy–Littlewood maximal function) といい,
をハーディ-リトルウッドの極大不等式 (Hardy–Littlewood maximal inequality) といいます。
測度の微分
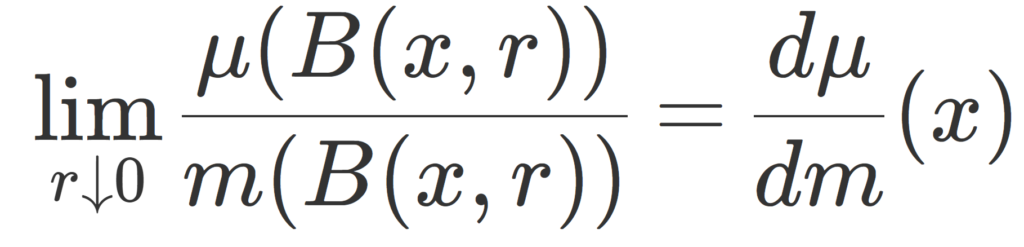
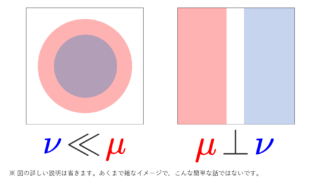
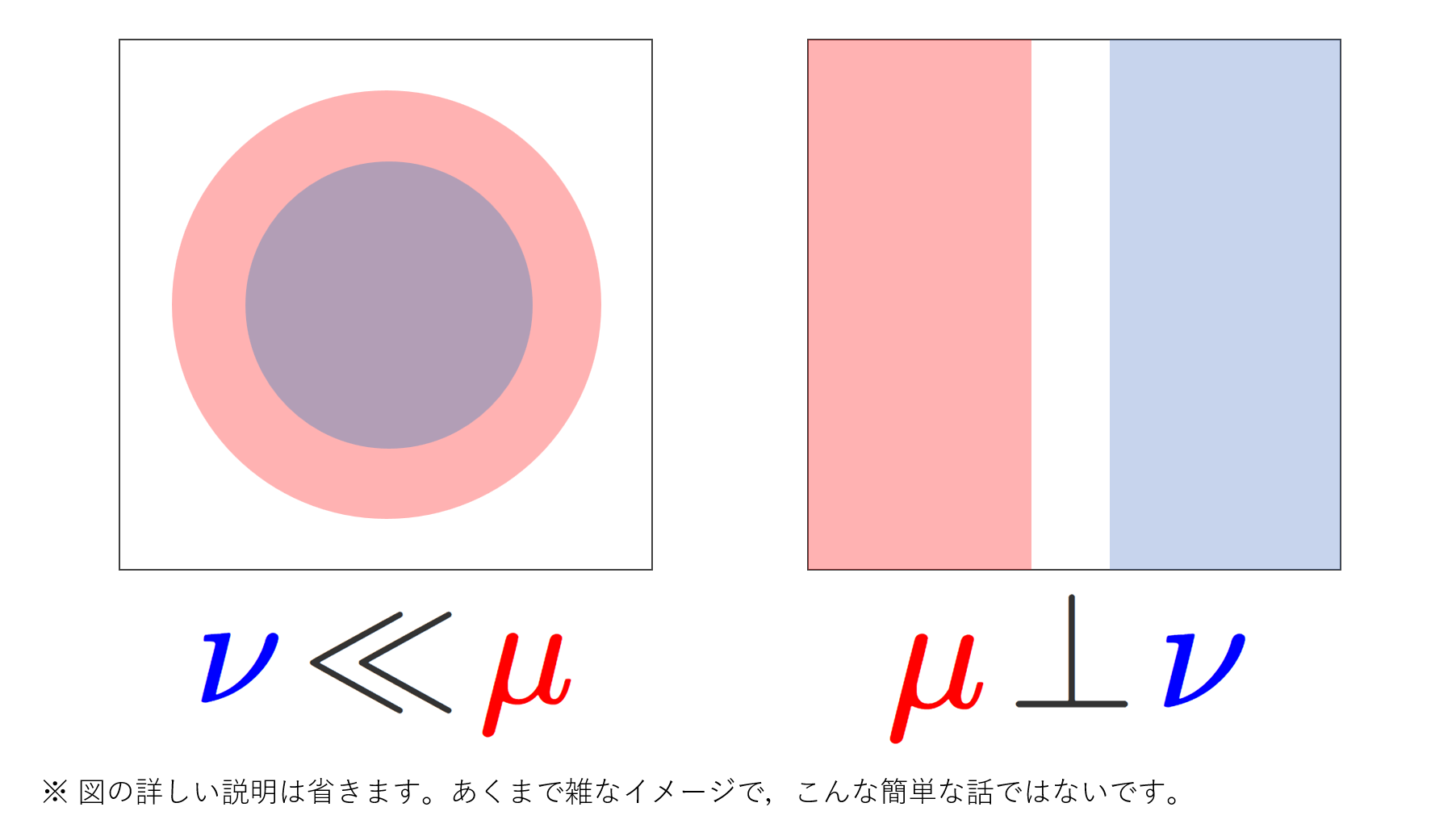
さっきまでは |\cdot | をルベーグ測度としていましたが,以下では, m をルベーグ測度とします。 \R^n において,m と絶対連続な測度と,特異な測度の微分を考えてみましょう。絶対連続な測度・特異な測度の定義は,以下で解説しています。
定理(測度の微分)
\R^n 上のルベーグ測度を m とする。σ有限な測度 \mu を m に対して絶対連続な測度(\mu\ll m )とし,σ有限な測度 \nu を m と特異な測度(\nu\perp m )とする。このとき, m\text{-a.e.} (ほとんどいたるところ)の x\in \R^n で
\color{red}\begin{aligned}\lim_{r\downarrow 0} \frac{\mu(B(x, r))}{m(B(x,r))} &=\frac{d\mu}{dm}(x), \\ \lim_{r\downarrow 0} \frac{\nu(B(x, r))}{m(B(x,r))} &=0 \end{aligned}
がそれぞれ成り立つ。ただし,関数 d\mu/dm はラドンニコディム微分とする。
ラドンニコディム微分が,本当に微分である,ということが分かる定理です。
証明しておきましょう。
証明
前半について
\mu\ll m より,ラドンニコディムの定理より,ラドンニコディム微分 f= d\mu/dm が存在して,
\mu(B(x,r)) = \int_{B(x,r)} f\, dm
とできる。ルベーグの微分定理より, m\text{-a.e.} で
後半について
\nu を有限測度として示す。σ有限なら,有限測度になるように全体空間を分割して考えることができるため,有限測度として示せば十分だからである。
\lambda, \varepsilon >0 とする。\nu \perp m であることと, \R^n 上の任意の有限測度は正則(内部正則)であることから,あるコンパクト集合 K\subset \R^n が存在して, m(K)=0, \; \nu(K) >\nu(\R^n)-\varepsilon とできる。
\begin{aligned}\overline{D}\nu(x)&= \limsup_{r\downarrow 0} \frac{\nu(B(x, r))}{m(B(x,r))},\\ M\nu(x)&=\sup_{0<r<\infty} \frac{\nu(B(x, r))}{m(B(x,r))} \end{aligned}
と定めると,示すべきは \overline{D}\nu(x)=0,\; m\text{-a.e.} である。 \nu_1(A)=\nu(A\cap K),\, A\in\mathcal{B}(\R^n) とし, \nu_2=\nu-\nu_1 とする。このとき,\nu_2(\R^n)<\varepsilon である。 x\in \R^n\setminus K のときは, \overline{D}\nu_1(x)=0 なので,
となる。したがって,
であり,両辺ルベーグ測度を考えると,m(K)=0 より,
ルベーグの微分定理の証明の後半において, \int_A f \,dx を \nu_2(A) に置き換えて全く同様に考えることで,
となる。したがって, m(\{\overline{D}\nu>\lambda\})\le 3^n \varepsilon/\lambda となって,左辺は \varepsilon に依らないから, m(\{\overline{D}\nu>\lambda\})=0 がわかる。 \lambda \downarrow 0 とすることで, \overline{D}\nu=0,\, m\text{-a.e.} である。
証明終
n=1 のとき,前半の \mu については,定理の主張をそのまま当てはめると
\lim_{h\downarrow 0} \frac{\mu((x-h, x+h))}{m((x-h, x+h))}=\frac{d\mu}{dm}(x),\quad m\text{-a.e.}
となりますが,一般に
であることと,定理「ルベーグの微分定理の1次元版」を用いることにより,
もわかりますね。 [x,x+h) を (x, x+h), (x-h, x), (x-h, x] 等に変えても同様です。
後半の \nu については
\lim_{h\downarrow 0} \frac{\nu((x-h, x+h))}{m((x-h, x+h))}=0,\quad m\text{-a.e.}
となりますが,
ですから,結局
が言えることになります。 [x,x+h) を (x, x+h), (x-h, x), (x-h, x] 等に変えても同様です。