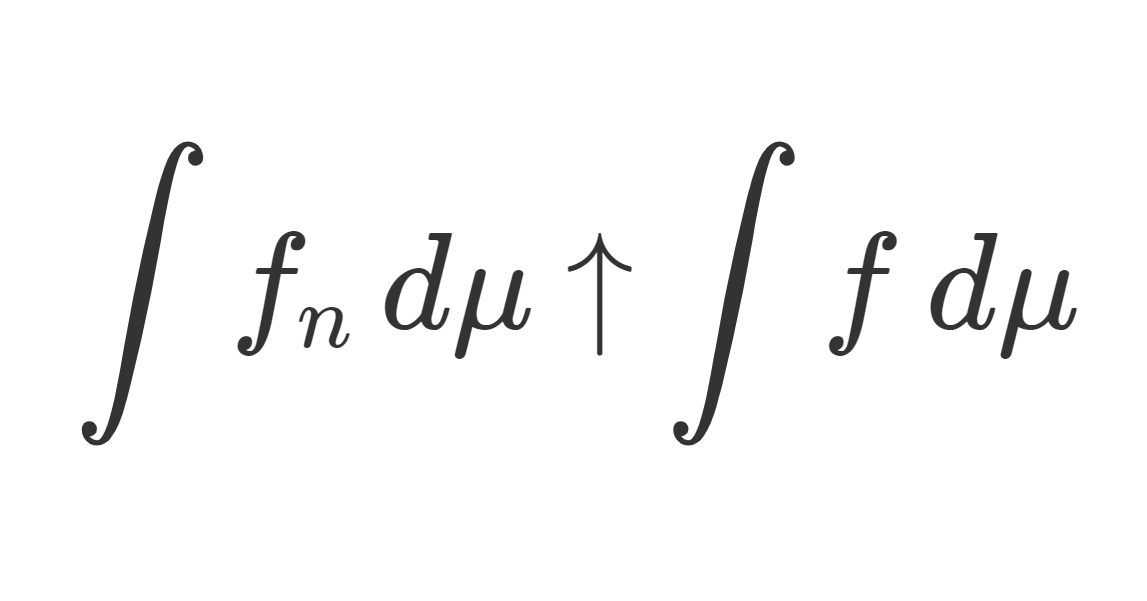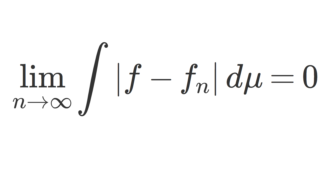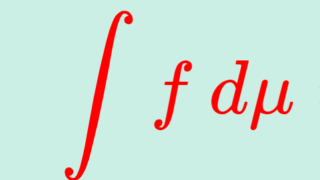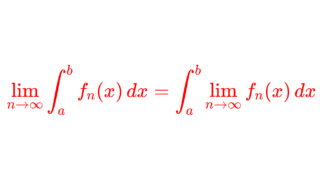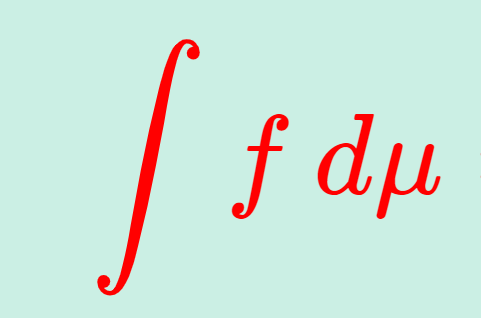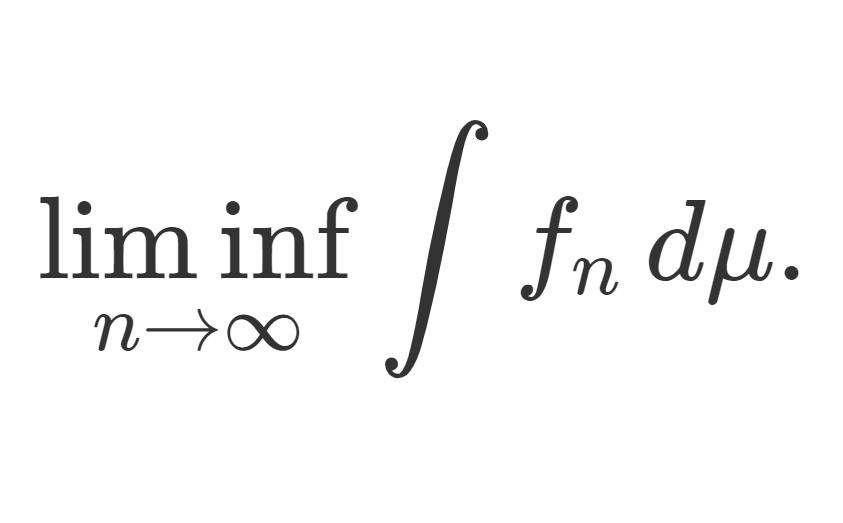測度論・ルベーグ積分における単調収束定理とは，非負可測関数の上昇列 \{f_n\} が f_n\uparrow f をみたすとき，
\lim_{n\to\infty} \int f_n \,d\mu = \int f\, d\mu
が成り立つという定理であり，ルベーグ積分における基本的かつ重要な収束定理の一つです。これについて，その主張と証明を行いましょう。
単調収束定理
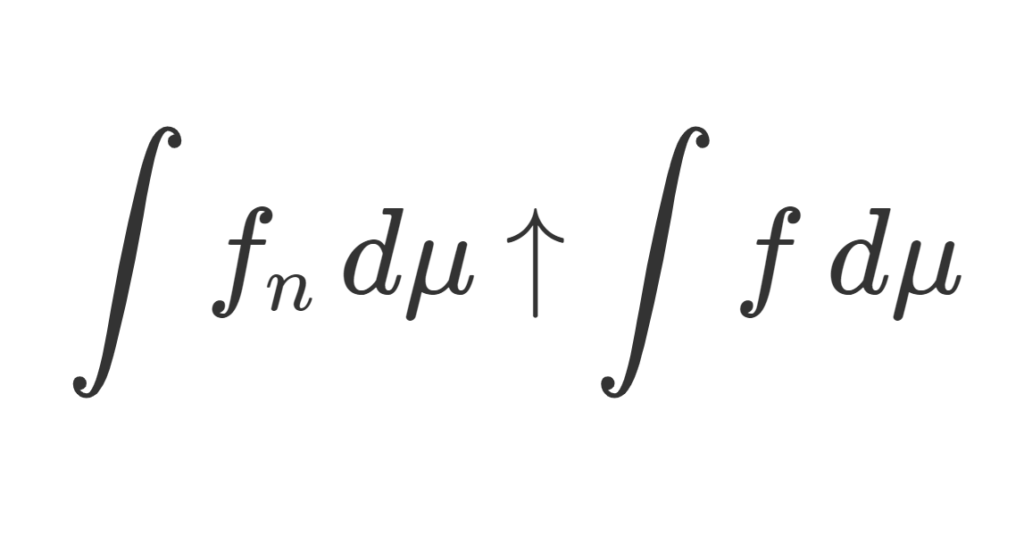
単調収束定理は英語で monotone convergence theorem のため，略して MCT といわれることもあります。単調収束定理の詳細を確認していきましょう。
広義単調増加で有界な数列は収束するという定理も，単調収束定理と呼ばれることがあります。これについては，以下で解説しています(本記事では扱いません)。
1. ルベーグの単調収束定理
以下で，「上昇列(増大列)」とは各点 x\in X で f_1(x)\le f_2(x)\le f_3(x)\le \dots を意味し， f_n\uparrow f とは \{ f_n\} が上昇列かつ各点 x\in X で f_n(x)\to f(x) を意味します。
定理1（ルベーグの単調収束定理）
(X,\mathcal{F}, \mu) を測度空間，\{ f_n\} はその上の非負可測関数の上昇列(増大列)とする。各点で f_n \uparrow f となるとき，
\color{red}\lim_{n\to\infty} \int f_n \,d\mu = \int f\, d\mu\in [0,\infty]
が成り立つ。
f の可測性は，可測関数列の極限より自動的に従うことに注意してください(→可測関数とは～定義と理解しておくべき大事な性質～)。等式を書き直すと，
\color{red} \lim_{n\to\infty} \int f_n \,d\mu = \int \lim_{n\to\infty} f_n \, d\mu
ですから，極限と積分の交換定理ですね。非負な上昇列なら交換可能だと言っているんですね。証明は最後に行いましょう。
なお，本定理は f_n \ge 0,\, \textcolor{red}{\mu\text{-a.e.}} かつ f_n \uparrow f,\, \textcolor{red}{\mu\text{-a.e.}} でも成立します(ほとんどいたるところ)。これも後で証明しましょう。
なお，定理の仮定から非負の条件を抜いてはいけません。実際， f_n =-1_{[n,\infty)} とすると， f_n \uparrow 0 ですが， \int_0^\infty f_n\, dx = -\infty \ne 0 となって，定理は成り立ちません。ただし， f_1\ge 0 を \int f_1\,d\mu>-\infty に置き換えるのはOKです。なぜなら， \{f_n -f_1\} として定理1を適用してから，結論の等式の両辺に \int f_1\,d\mu を加えればよいからです。
2. 積分と和の交換
単調収束定理から直ちに，以下の定理が導けます。項別積分が全体の積分に一致する定理です。
定理2（積分と和の交換）
\{f_n\} を非負可測関数の列とする。このとき，
\color{red} \sum_{n=1}^\infty\int f_n \, d\mu = \int \sum_{n=1}^\infty f_n \, d\mu \in [0,\infty]
が成り立つ。
これの証明は， g_n =\sum_{k=1}^n f_k, \, g=\sum_{k=1}^\infty f_k とすれば， g_n \uparrow g となって，定理1に帰着できますね。
単調収束定理の具体例・応用
証明の前に，単調収束定理の具体例・応用を挙げましょう。
例1.
1/(1+x^n) は [0,1) 上非負かつ n について広義単調増加である。よって単調収束定理より，
\begin{aligned}&\lim_{n\to\infty} \int_{[0,1) }\frac{1}{1+x^n} \,d\mu(x) \\&= \int_{[0,1)} \lim_{n\to\infty} \frac{1}{1+x^n} \,d\mu(x) \\&=\int_{[0,1)} \,d\mu(x) = \mu([0,1)).\end{aligned}例2.
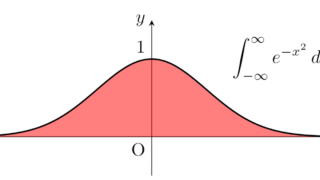
f_n(x) = (1-x^2/n)^n1_{[0,\sqrt{n}]} とおくと，これは f_n \ge 0 かつ \{f_n\} は [0,\infty) 上の上昇列(増大列)で， f_n \uparrow e^{-x^2} なので，単調収束定理より
\lim_{n\to\infty} \int_0^{\sqrt{n}} \left(1-\frac{x^2}{n}\right)^n\, dx = \int_0^\infty e^{-x^2}\,dx.ここで，左辺の積分は x=\sqrt{n} \cos\theta で置換することで
\begin{align} &\int_0^{\sqrt{n}} \left(1-\frac{x^2}{n}\right)^n\, dx \\&= \int_{\pi/2}^0 \sin^{2n}\theta \sqrt{n} (-\sin\theta)\,d\theta \\ &= \sqrt{n} \int_0^{\pi/2} \sin^{2n+1}\theta\,d\theta \end{align}
であり，ウォリス積分より，(3)= \sqrt{n} \frac{(2n)!!}{(2n+1)!!} です。これとウォリスの公式より，
もわかりますから，結局ガウス積分 \int_0^\infty e^{-x^2}\,dx = \sqrt{\pi}/2 が証明できたことになります。
ガウス積分のさまざまな証明は以下で扱っています。
例3.
f \ge 0 を可測関数とする。このとき，
\lim_{q\downarrow 0} \int e^{-qx} f(x)\, d\mu(x) = \int f(x) \, d\mu(x).厳密には，単調収束定理は「列の極限の定理」より，実数列 \{q_n\} を q_n \downarrow 0\; (n\uparrow \infty) となるようにしないと適用できません。しかし，はさみうちの原理より明らかに q\downarrow 0 で成り立つことが分かるでしょう。
ルベーグの単調収束定理の証明
上で述べた定理1.を
- 各点ver.
- a.e. ver.
と段階を踏んで証明しておきましょう。
各点ver. の証明
証明する定理を再掲しましょう。
定理1再掲
(X,\mathcal{F},\mu) を測度空間， \{f_n\} はその上の非負可測関数の上昇列(増大列)とする。各点で f_n \uparrow f とするとき，
\color{red} \lim_{n\to\infty} \int f_n \,d\mu = \int f\,d\mu.
もともと非負可測関数のルベーグ積分は，単関数を下から近似する形で定義しました(→【数学科向け】ルベーグ積分の定義を段階を踏んで解説する)。
本定理も，単関数ではないですが，下から近似するという点は同じです。そう考えれば，ある意味当たり前の定理といえるでしょう。証明は対角線論法です。
証明
f_n\le f より， \int f_n \,d\mu \le \int f\,d\mu であることと， \{f_n\} は上昇列(増大列)より \lim_{n\to\infty} \int f_n\, d\mu が存在することに注意して
\begin{equation} \lim_{n\to\infty} \int f_n \,d\mu\le \int f\, d\mu \end{equation}
が成り立つ。
各 f_n を下から近似する非負単関数の上昇列(増大列) \{g_{n,m}\}_m をとる(これが可能であることは単関数とは何か～定義と可測関数の単関数近似～でやった)。 すなわち， g_{n,m} は単関数であり， g_{n,m} \uparrow_m f_n である。
h_{n,m} =\sup_{k\le n} g_{k,m} と定めると， \{h_{n,m}\}_m も f_n を下から近似する単関数の上昇列(増大列)になる。
\begin{equation}\int f_n \, d\mu \ge \int h_{n,n} \, d\mu\end{equation}
であることと，非負単関数列 \{h_{n,n}\}_n が h_{n,n}\uparrow f となることに注意して， (5) 式の両辺 n\to\infty とすると，
となる(右辺の収束は非負可測関数におけるルベーグ積分の定義・定理で扱った)。 (4),(6) 式より，証明が終わる。
証明終
a.e. ver. の証明
各点で f_n \ge 0 かつ f_n \uparrow f の部分は， \mu\text{-a.e.} にしても良いといいました。これについても証明しておきましょう。定理は以下です。
定理1 a.e. ver
(X,\mathcal{F},\mu) を測度空間， \{f_n\} はその上の可測関数で f_n \ge 0, \, \mu\text{-a.e.} とする。 f_n \uparrow f ,\, \mu\text{-a.e.} とするとき，
\color{red} \lim_{n\to\infty} \int f_n \,d\mu = \int f\,d\mu.
証明
A = \left(\bigcap_{n=1}^\infty \{ f_n \ge 0\}\right)\cap \{ f_n \uparrow f\}
とすると， \mu(f_n < 0) =\mu(f_n \not\,\uparrow f)=0 と測度の劣加法性より， \mu(A^c)=0 である。
\tilde{f_n} = f_n 1_A ,\; \tilde{f} = f1_A と定めると， \tilde{f_n}=f_n, \; \tilde{f}=f,\; \mu\text{-a.e.} であり， \{\tilde{f_n}\}, \,\tilde{f} に対しては各点ver.の単調収束定理が使えるので，
\begin{aligned} \lim_{n\to\infty}\int f_n\,d\mu &= \lim_{n\to\infty}\int \tilde{f_n}\,d\mu \\ &= \int \tilde{f}\,d\mu\\ &= \int f\,d\mu.\end{aligned}証明終
無事証明できましたね。
