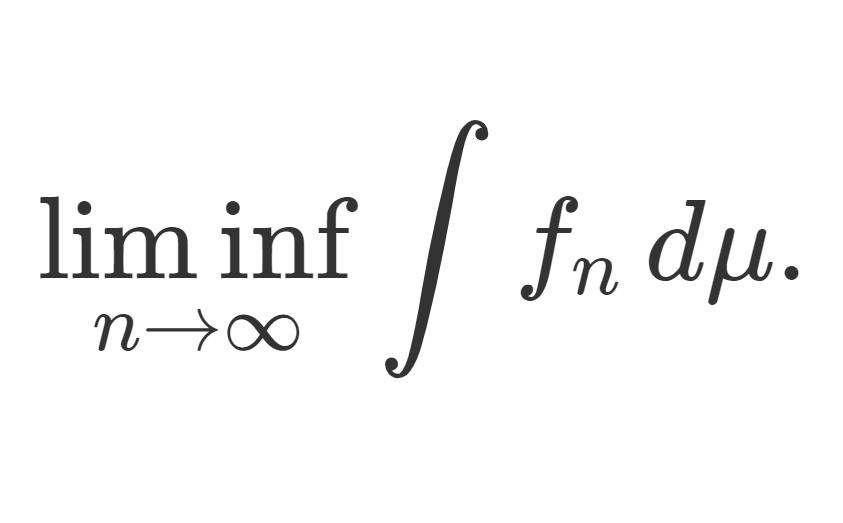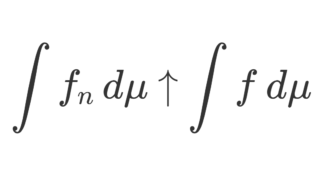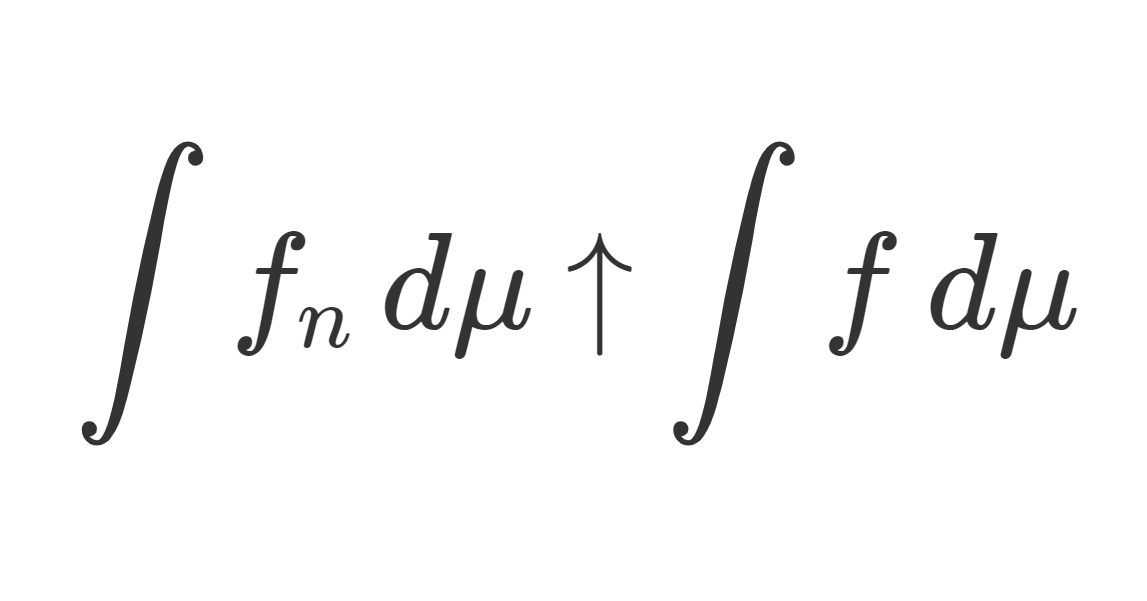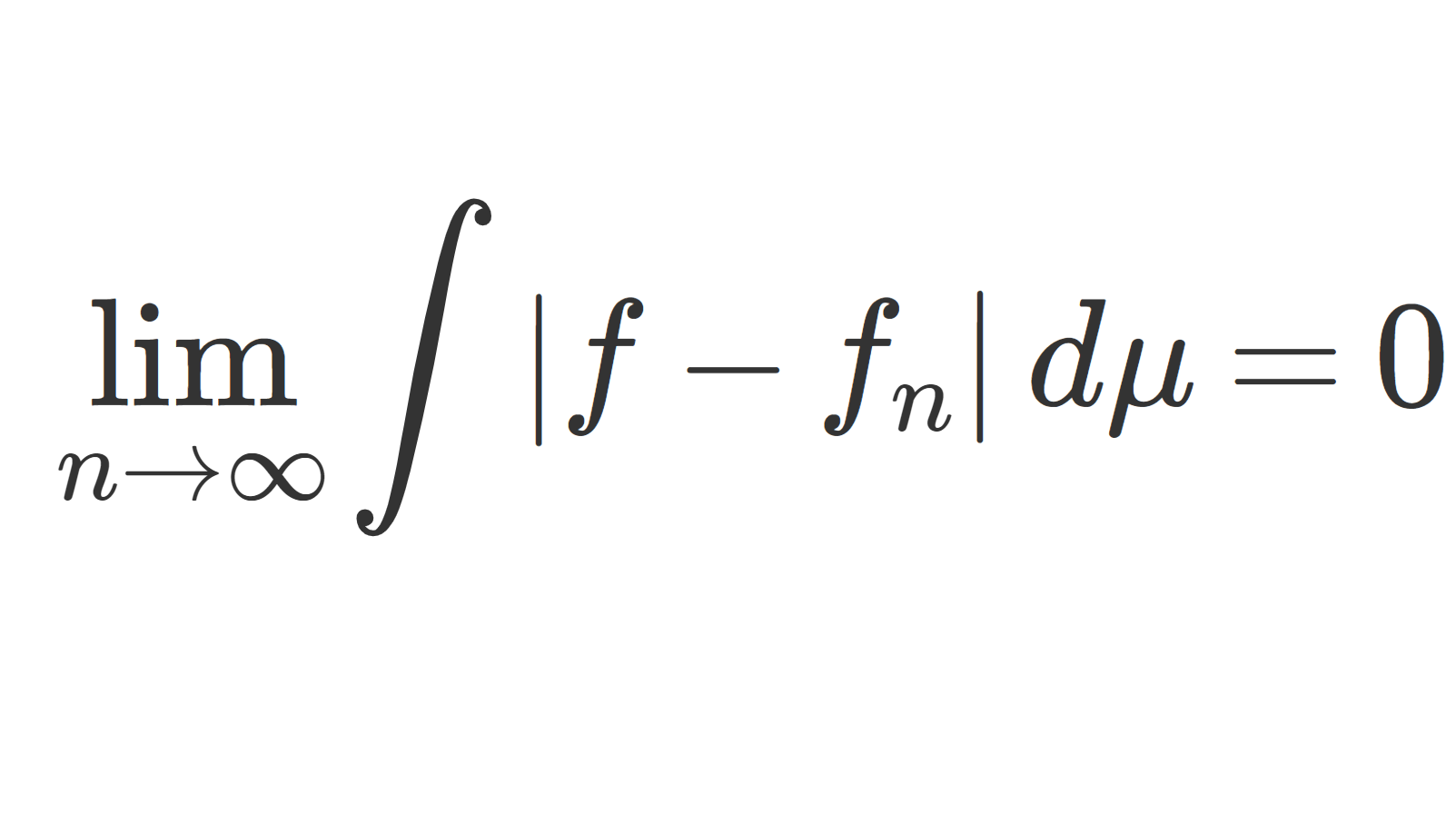測度論・ルベーグ積分におけるFatouの補題 (Fatou’s lemma;ファトウの補題) は,収束定理の中で大事な定理の一つです。Fatouの補題について,その主張と証明,活用例・具体例を解説していきましょう。
Fatouの補題とその証明
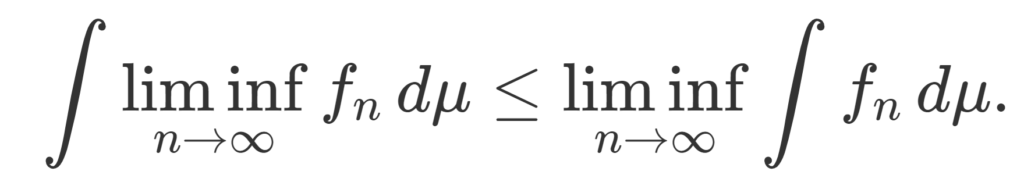
Fatouの補題の主張
Fatouの補題
(X,\mathcal{F},\mu) を測度空間とし, \{f_n\} をその上の非負可測関数列とする。このとき,
\color{red}\int \liminf_{n\to\infty}f_n\,d\mu\le \liminf_{n\to\infty} \int f_n \,d\mu.先に \liminf を取ってから積分する方が,積分してから \liminf を取るよりも小さくなるという定理ですね。どちらかあるいは両方の辺が無限大になっても構いません。
定理の仮定で,非負の条件は外せません。たとえば, f_n = -1_{[n,\infty)} と定めると, \liminf f_n =0 ですが, \liminf \int f_n \,dx = -\infty となって不等号が逆転しています。
ただし, f_n\ge 0 を f_n\ge g かつ \int g\,d\mu>-\infty に置き換えるのはOKです。なぜなら, \{f_n -g\} として上の補題を適用してから,結論の等式の両辺に \int g\,d\mu を加えればよいからです。
なお, f_n \ge 0 は各点ではなく, f_n \ge 0,\, \textcolor{red}{\mu\text{-a.e.}} (ほとんどいたるところ)でも構いません。各 f_n において,測度0の集合(零集合)上の値は 0 に修正して各点で f_n \ge 0 と思っても積分の値に影響を及ぼさないからです。詳しい議論は省略しますが,単調収束定理のときの証明と同様にやればよいです。
Fatouの補題の証明
証明には単調収束定理(MCT)を用います。振り返っておきましょう。
\{f_n\} を非負可測関数の上昇列(増大列)とし, f_n \uparrow f とするとき,
\lim_{n\to\infty} \int f_n \,d\mu=\int f\,d\mu.これの証明は以下で行っています。
これを認めて証明しましょう。
証明
g_n =\inf_{k\ge n} f_k とおくと, \{g_n\} は非負可測関数の上昇列(増大列)で, g_n \uparrow \liminf f_n である(liminfの定義そのままである)。したがって単調収束定理より,
\begin{equation}\lim_{n\to\infty} \int g_n \,d\mu=\int \liminf_{n\to\infty} f_n \,d\mu.\end{equation}
一方で, g_n \le f_n より \int g_n \,d\mu\le \int f_n \,d\mu であるから,両辺 \liminf を取ることで,
(1),(2) 式より,求めたい式
を得る。
証明終
Fatouの補題の具体例・活用例
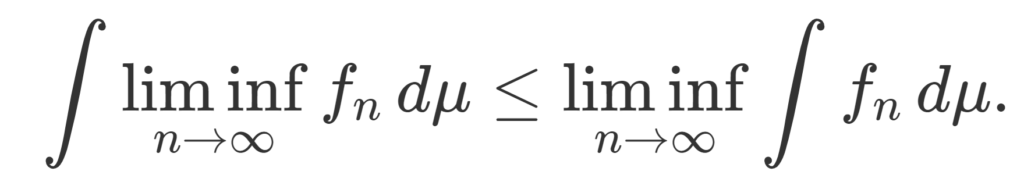
例1.
f_n = 1_{[n,n+1]} とすると,f_n \ge 0,\; \liminf_{n\to\infty} f_n =0, \; \int f_n \,dx = 1 より,
\begin{aligned}&\int \liminf_{n\to\infty}f_n \,dx = 0,\\ &\liminf_{n\to\infty} \int f_n \,dx= 1. \end{aligned}
0<1 より,確かにFatouの補題が成立する。
Fatouの補題で真の不等号が成り立つ例ですね。
例2.
\{f_n\} は可測関数列で, f=\lim_{n\to\infty} f_n かつ \liminf_{n\to\infty}\int |f_n| \,d\mu<\infty とする。このとき,Fatouの補題より,
\begin{aligned}\int |f|\,d\mu &= \int \liminf_{n\to\infty} |f_n|\,d\mu \\ &\le \liminf_{n\to\infty} \int |f_n| \,d\mu <\infty \end{aligned}
より, f は可積分である。
Fatouの補題は,可積分性の判定に使うことができるわけですね。
例3.
t>0, \, x>1 に対して (1-\cos tx)/t^2x^3 \ge 0 であるから,Fatouの補題より
\begin{aligned}&\liminf_{t\downarrow 0} \int_1^\infty \frac{1-\cos tx}{t^2x^3} \,dx \\&\ge \int_1^\infty \liminf_{t\downarrow 0} \frac{1-\cos tx}{t^2x^3} \,dx\\ &=\int_1^\infty \frac{1}{2x}\,dx =\infty. \end{aligned}
したがって,
が証明される。
上のように,Fatouの補題を \ge 向きに使うことで,積分の極限が発散することを証明できますね。
\displaystyle \lim_{t\downarrow 0} \frac{1-\cos tx}{t^2x^3} の計算はロピタルの定理を使えばよいです。
なお,Fatouの補題は「列の極限の定理」より, \{t_n\} を t_n \downarrow 0 \; (n\uparrow \infty) となるようにとって適用せねばなりません。今回の場合は,どんな点列 \{ t_n\} をとっても,極限が無限大に発散することが言えますから,結局 t\downarrow 0 の極限が無限大に発散することが言えるわけですね。