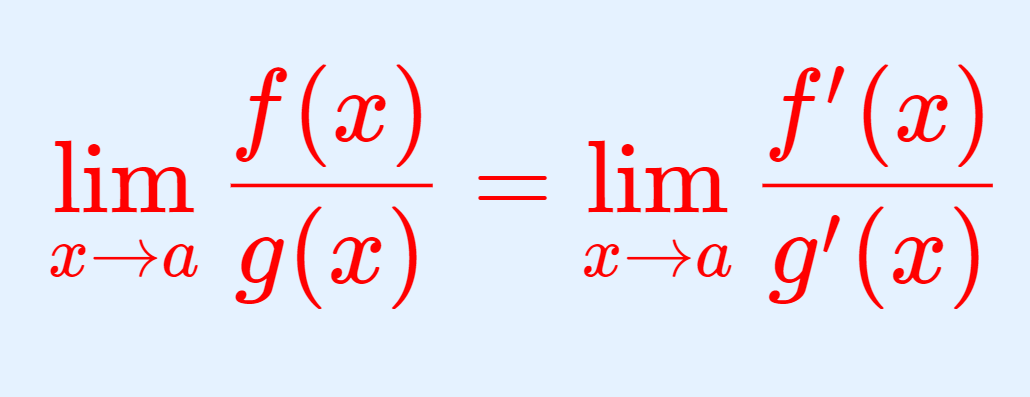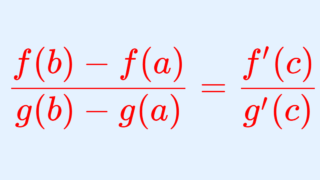ロピタルの定理を誤りなく使おう～具体例6つと証明～

ロピタルの定理と言えば，適用条件が難しく，使うときは注意せよといわれる定理の1つでしょう。今回はロピタルの定理について，その主張と成り立つ・成り立たない例を確認し，最後に証明を述べることにしましょう。

ロピタルの定理の主張
ロピタルの定理の具体例
1. ロピタルの定理が適用できる例
2. ロピタルの定理が適用できない例
ロピタルの定理の証明
1. 0/0 型の証明
2. ∞/∞ 型の証明
さいごに
参考

ロピタルの定理の主張

まずはロピタルの定理の厳密な主張を確認しましょう。

ロピタルの定理（l’Hôpital’s rule）

$-\infty \le a \le \infty$ とする。( $a$ でない) $a$ の近く(近傍)で微分可能な関数 $f, g$ が

$\displaystyle\lim_{x\to a} f(x) = \lim_{x \to a} g(x)$ が $0$ または $\pm\infty$ であり，
( $a$ を除く) $a$ の近くで $g'(x) \ne 0$ であり，
$\displaystyle \lim_{x\to a}\dfrac{f'(x)}{g'(x)} \in [-\infty, \infty]$ が存在するならば，

\color{red}\lim_{x\to a} \frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)}

が成立する。

少し前提条件が多いので，難しい定理ですよね。正直に言うと，自分もこの条件をちゃんと覚えているわけではなく，使う度に調べています(笑)。なお，この3つの条件のうち，どれか一つでも欠けてはいけません。次の具体例のところで確認しましょう。

$0/0, \infty/\infty$ というのは，不定形と呼ばれる極限の形です。ロピタルの定理とは「不定形の極限を微分の極限を用いて述べよう」という，そういう定理です。

$g(x), g'(x)$ はともに分母にあるにもかかわらず， $g'(x)$ のみ $0$ にならないことを確認していて， $g(x)$ は $0$ にならないことを確認しなくてもよいのか，と思ったかもしれません。

これは $\lim_{x\to a}g(x) = \pm \infty$ のときは心配ありませんし， $\lim_{x\to a} g(x) = 0, \,-\infty<a<\infty$ のときも，必要ならば $g(a)=0$ と， $g$ が連続になるよう定義し直してロルの定理（平均値の定理）から背理法で矛盾を導くことにより $a$ でない $a$ の近くで $g(x) \ne 0$ であることが従います。
また， $a=\pm\infty$ のときは， $g'$ の条件から $g(x)$ は十分大きいところで狭義単調になりますから，こちらも問題ありません。

なお，主張における $x \to a$ の部分は片側極限 $x \to a\pm$ としても同様です。

ロピタルの定理の具体例

ロピタルの定理が適用できる例と適用できない例を順番に確認していきましょう。

ロピタルの定理が適用できる例

ロピタルの定理の成立には

$\displaystyle\lim_{x\to a} f(x) = \lim_{x \to a} g(x)$ が $0$ または $\pm\infty$ であり，
( $a$ を除く) $a$ の近くで $g'(x) \ne 0$ であり，
$\lim_{x\to a}\dfrac{f'(x)}{g'(x)} \in [-\infty, \infty]$ が存在するならば，

という3つの条件が必要でした。これらのすべての条件をみたし，ロピタルの定理が適用できる例をいくつか紹介しましょう。

例1.

\color{red}\lim_{x\to 0} \frac{1-\cos x}{x^2} =\lim_{x\to 0} \frac{\sin x }{2x} = \frac{1}{2}.

$0/0$ 型の不定形です。 $f(x) = 1-\cos x, \, g(x) = x^2$ とおくと，上の条件3つとも成立していることが分かりますね。

例2.

\color{red} \lim_{x\to\infty} \frac{e^x}{x^2} = \lim_{x\to\infty} \frac{e^x}{2x} = \lim_{x\to\infty} \frac{e^x}{2} = \infty.

$\infty/\infty$ 型の不定形です。ロピタルの定理を複数回使っていることに注意してください。

具体的には， $f(x) = e^x, \,g(x) =2x$ とおいて，2つ目の等式にロピタルの定理を適用した後に， $f(x) =e^x, \, g(x) = x^2$ とおいて，1つ目の等式にロピタルの定理を適用しています。

例3.

$a, b> 0$ とするとき，

\color{red}\begin{aligned}\lim_{x\to 0} \frac{a^x - b^x }{x} &= \lim_{x\to 0} \frac{a^x \log a - b^x \log b}{1}\\ & = \log\frac{a}{b}. \end{aligned}

2つ目の等式はロピタルの定理ではなく，ただの計算です。

ロピタルの定理が適用できない例

もう一度復習すると，ロピタルの定理の成立には

$\displaystyle \lim_{x\to a} f(x) = \lim_{x \to a} g(x)$ が $0$ または $\pm\infty$ であり，
( $a$ を除く) $a$ の近くで $g'(x) \ne 0$ であり，
$\displaystyle \lim_{x\to a}\dfrac{f'(x)}{g'(x)} \in [-\infty, \infty]$ が存在するならば，

という3つの条件が必要でした。ここでは，これらの条件を一つでもみたさないと，ロピタルの定理が使えないことを確認しましょう。

1. lim f(x) = lim g(x) = 0, ±∞ をみたさないもの

例4.

$\color{red} f(x) = x, \,g(x) = x+1$ とし， $x \to 0$ を考えると，条件2,3をみたすが1をみたさない。このとき，

\lim_{x\to 0} \frac{f(x)}{g(x)} = \lim_{x\to 0} \frac{x}{x+1} = 0

であるが，

\lim_{x\to 0} \frac{f'(x)}{g'(x)} = \lim_{x\to 0} \frac{1}{1}= 1

なので， $\displaystyle \lim_{x\to 0} \frac{f(x)}{g(x)} \ne \lim_{x\to 0} \frac{f'(x)}{g'(x)}$ である。

$\lim_{x\to 0} g(x) = 1\ne 0$
$g'(x) = 1 \ne 0$
$\lim_{x\to 0} \frac{f'(x)}{g'(x)} = \lim_{x\to 0} \frac{1}{1}= 1$

なので，確かに上の黄色枠の条件2,3は成立しますが，条件1は成立しません。

2. a の近くで g'(x) ≠ 0 をみたさないもの

例5.

$\color{red} f(x) =x + \sin x \cos x, \, g(x) = e^{\sin x} (x+ \sin x \cos x )$ とし， $x\to\infty$ を考えると，条件1,3はみたすが，2はみたさない。このとき，

\lim_{x\to \infty} \frac{f(x)}{g(x)} = \lim_{x\to \infty} \frac{1}{e^{\sin x}}

となり，これは振動して収束しないが，

\begin{aligned}&\lim_{x\to \infty} \frac{f'(x)}{g'(x)} \\ &= \lim_{x\to \infty} \frac{2\cos^2 x}{e^{\sin x} \cos x(x+\sin x \cos x + 2 \cos x)}\\ &= 0\end{aligned}

なので， $\displaystyle \lim_{x\to \infty} \frac{f(x)}{g(x)} \ne \lim_{x\to \infty} \frac{f'(x)}{g'(x)}$ である。

$\lim_{x\to \infty} f(x) \lim_{x\to\infty} g(x) = \infty$
$g'(x) = e^{\sin x} \cos x(x+\sin x \cos x + 2\cos x )$ より， $x= (\frac{1}{2}+n)\pi \, (n=0,1,2,\ldots)$ のとき $g'(x) = 0 .$
$\lim_{x\to 0} \frac{f'(x)}{g'(x)} =0$

なので，確かにロピタルの定理の条件1,3は成立しますが，条件2は成立しません。

3. lim f'(x)/g'(x) が存在しないもの

例6.

$\color{red} f(x) = \sin x +x, \, g(x) = x$ とおき， $x \to \infty$ を考えると，条件1,2をみたすが3をみたさない。このとき，

\lim_{x\to \infty} \frac{f(x)}{g(x)} = \lim_{x\to \infty} \frac{\sin x + x}{x} = 1

であるが，

\lim_{x\to \infty} \frac{f'(x)}{g'(x)} = \lim_{x\to \infty} \frac{\cos x + 1}{1}

は振動して収束せず， $\displaystyle \lim_{x\to \infty} \frac{f(x)}{g(x)} \ne \lim_{x\to \infty} \frac{f'(x)}{g'(x)}$ である。

$\lim_{x\to\infty} f(x) = \lim_{x\to\infty} g(x) =\infty$
$g'(x) = 1 \ne 0$
$\lim_{x\to\infty} \frac{f'(x)}{g'(x)}$ は存在しない

ので，確かに条件1,2をみたしますが，条件3はみたしません。

なお， $f(x) = \sin (1/x) +1/x, \, g(x) = 1/x$ とおくと， $x \to 0+$ の場合の反例になります。

3つのどの条件も欠けてはいけないことが分かりましたね。

ロピタルの定理の証明

最後にロピタルの定理の証明を行いましょう。証明には，コーシーの平均値の定理が必要になります。まずはそれの復習を行います。

コーシーの平均値の定理

関数 $f,g$ は閉区間 $[a,b]$ で連続かつ開区間 $(a, b)$ で微分可能であるとする。このとき， $g'(x) \ne 0 \,\,(a < x < b)$ ならば，

\color{red} \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)} , \quad a < c< b

となる $c$ が存在する。

ここでコーシーの平均値の定理には，ロピタルの定理でいう条件2，すなわち ( $a$ を除く) $a$ の近くで $g'(x) \ne 0$ であることを使っています。ロピタルの定理の条件2は，コーシーの平均値の定理から来るものなわけです。

コーシーの平均値の定理は，以下で解説しています。

では，ロピタルの定理の証明にうつりましょう。証明は

$0/0$ 型
$\infty/\infty$ 型

に分けて行います。（ $-\infty /-\infty$ 型は2つ目と同様なので省略します。）それぞれにおいて，ロピタルの定理の必須の条件

$\displaystyle \lim_{x\to a} f(x) = \lim_{x \to a} g(x)$ が $0$ または $\pm\infty$ であり，
( $a$ を除く) $a$ の近くで $g'(x) \ne 0$ であり，
$\displaystyle \lim_{x\to a}\dfrac{f'(x)}{g'(x)} \in [-\infty, \infty]$ が存在するならば，

をどこで使っているのか確認しながら進めていきましょう。

0/0 型の証明

証明

$-\infty < a < \infty$ のとき

$f(a)=g(a)=0$ と必要に応じて定め直すことで， $f, g$ は $a$ の近くで連続， $a$ を除く $a$ の近くで微分可能と思ってよい。コーシーの平均値の定理より， $a$ の近くの $x \ne a$ において，

\frac{f(x)-f(a)}{g(x)-g(a)} = \frac{f'(c_x)}{g'(c_x)}

となる $a < c_x < x$ または $x < c_x < a$ が存在する。特に， $f(a)=g(a) = 0$ であったから，

\frac{f(x)}{g(x)} = \frac{f'(c_x)}{g'(c_x)}

である。 $x\to a$ とすると， $c_x \to a$ であることに注意する。右辺は $c_x \to a$ のときの極限が存在するから，

\lim_{x\to a} \frac{f(x)}{g(x)} = \lim_{x\to a} \frac{f'(x)}{g'(x)}

であり，定理が示された。近づけるのを片側からのみにすることで， $x\to a+, x\to a-$ としても問題ないことがすぐわかる。

$a =\pm\infty$ のとき $a= \infty$ のときのみ示す。

$F(x) = f(1/x), G(x) = g(1/x)$ とおいて上の場合に帰着させる。実際，

F'(x) = -\frac{1}{x^2}f' \!\left(\frac{1}{x}\right), \,\, G'(x) = -\frac{1}{x^2}g' \!\left(\frac{1}{x}\right)

であるから， $F'(x)/G'(x) = f'(1/x)/g'(1/x)$ なので

\begin{aligned}\lim_{x\to \infty} \frac{f(x)}{g(x)} &= \lim_{x\to 0+ } \frac{F(x)}{G(x)} \\ &= \lim_{x\to 0+} \frac{F'(x)}{G'(x)} \\ &= \lim_{x\to \infty } \frac{f'(x)}{g'(x)}\end{aligned}

であることから従う。ただし，2番目の等式は $a\to 0+$ の場合のロピタルの定理を用いた。

証明終

$f(a)=g(a)=0$ として計算を進めているところに条件1.を，コーシーの平均値の定理に条件2.を， $\displaystyle \lim_{x\to a } \dfrac{f'(c_x)}{g(c_x)}$ の存在性に条件3.を使っていますね。

∞/∞ 型の証明

こちらは関数の極限の定義である，イプシロンデルタ論法を明示的に使います(→イプシロンデルタ論法をわかりやすく丁寧に～関数の極限の定義～)。

証明

$-\infty < a < \infty$ のとき $x \to a+$ の方のみ示すことにする。

$\varepsilon > 0$ とおく。 $\displaystyle \lim_{x\to a} \dfrac{f'(x)}{g'(x)} = L$ とすると， $\delta > 0$ が存在して，

|x-a|< \delta \implies \left|\dfrac{f'(x)}{g'(x)} -L \right| < \varepsilon

とできる。ここで， $0<b-a < \delta$ となる $b$ を一つ固定しよう。コーシーの平均値の定理により， $a<x<b$ とすると，

\frac{f(x)-f(b)}{g(x)-g(b)} = \frac{f'(c_x)}{g'(c_x)}

となる $x< c_x < b$ が存在する。上の式を変形し，さらに $\lim_{x\to a+ } f(x) = \lim_{x\to a+ } g(x) = \infty$ なので，

\begin{aligned} \frac{f(x)}{g(x)} - \frac{f'(c_x)}{g'(c_x)}&= \frac{f'(c_x)}{g'(c_x)}\left( \frac{1-\frac{g(b)}{g(x)}}{1-\frac{f(b)}{f(x)}} -1 \right) \\ &\xrightarrow{x\to a+} 0 \end{aligned}

となる。よってある $\delta' > 0$ が存在して， $a<x< a+\delta'$ ならば

\left|\frac{f(x)}{g(x)} - \frac{f'(c_x)}{g'(c_x)}\right| < \varepsilon

とできる。三角不等式により， $a<x<a+\min\{\delta,\delta'\}$ をみたす任意の $x$ に対して，

\begin{aligned} &\left|\frac{f(x)}{g(x)}-L\right|\\ &\le \left|\frac{f(x)}{g(x)} - \frac{f'(c_x)}{g'(c_x)}\right| + \left| \frac{f'(c_x)}{g'(c_x)} - L\right| \\ &\le \varepsilon + \varepsilon = 2\varepsilon \end{aligned}

であるから，とくに $\displaystyle \lim_{x\to a+}\dfrac{f(x)}{g(x)} = L = \lim_{x\to a+}\dfrac{f'(x)}{g'(x)}$ が分かった。

$a =\pm\infty$ のとき $a= \infty$ のときのみ示す。

$F(x) = f(1/x), G(x) = g(1/x)$ とおいて上の場合に帰着させて， $0/0$ 型のときと同様であるから，省略する。

証明終

$\lim_{x\to a}f(x)=\lim_{x\to a}g(x)=\infty$ として計算を進めているところに条件1.を，コーシーの平均値の定理に条件2.を， $\displaystyle\lim_{x\to a } \dfrac{f'(x)}{g'(x)} = L$ としているところに条件3.を使っていますね。