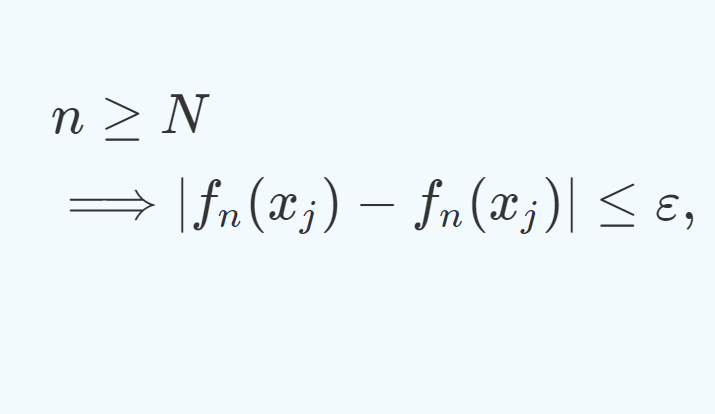関数列が各点収束するとき，同程度連続であれば，それが一様収束であるという定理を紹介し，証明します。
各点収束と一様収束の違いは以下の定理を確認してください。本記事はこれを既知とします。
定理～各点収束+同程度連続 = 一様収束～
定理
\{f_n\colon [0, 1] \to \mathbb{R} \} を同程度連続な関数列とし， f \colon [0, 1] \to \mathbb{R} に各点収束するとする。
このとき，この収束は一様収束である。
定理の証明の前に，同程度連続の定義を復習しておきましょう。
定義（同程度連続性）
関数列 \{f_n\} が同程度連続（同等連続, equi-continuous）であるとは，任意の \varepsilon >0 に対し，ある \delta > 0 が存在して，任意の n に対して
|x-y| < \delta \Rightarrow |f_n(x) - f_n(y) | < \varepsilon
が成立することである。
連続は連続でも，n によらずに「均一に」連続であることを同程度連続というんですね。
なお，「同程度連続性」についてはこの定理よりも，アスコリ－アルツェラの定理 (Ascoli-Arzelà theorem) が有名です。今回の定理はこれの系と言ってもよいでしょう。アスコリ－アルツェラの定理は，以下の記事を参照してください。
証明
早速証明に入りましょう。
証明
\varepsilon > 0 とする。同程度連続性より，ある \delta > 0 が存在して，
\begin{aligned} &|x-y| < \delta \\ &\Longrightarrow |f_n(x) - f_n(y)| \le \varepsilon, \,\, (n\ge 1) \end{aligned}が成立する。特に，この式で n \to \infty とすることで，
\begin{aligned} & |x-y| < \delta \\ &\Longrightarrow |f(x) - f(y)| \le \varepsilon, \,\, (n\ge 1) \end{aligned}ここで， 0 = x_1 < x_2 < x_3 < \cdots < x_m = 1 を |x_j - x_{j+1} | < \delta\,\,(1\le j \le m-1) をみたすように取る。
各点収束することから，ある N \ge 1 が存在して，
とできる。
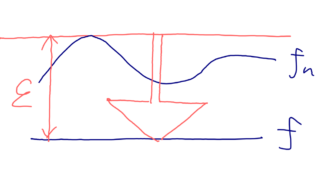
任意の x \in [0, 1] を固定する。このとき， x_1, x_2, \ldots, x_m から x に一番近い点 x_j を固定することで， n\ge N のとき
\begin{aligned} &|f_n(x) - f(x)| \\ &\le |f_n(x) - f_n(x_j)| \\ &+ |f_n(x_j) - f(x_j)| \\ &+ |f(x_j) - f(x)| \\ &\le \varepsilon + \varepsilon + \varepsilon = 3\varepsilon \end{aligned}よって，一様収束する。
証明終
類似の定理
各点収束から一様収束が従う定理としては，ディニの定理 (Dini’s theorem) が有名です。これについては，以下を参照してください。
