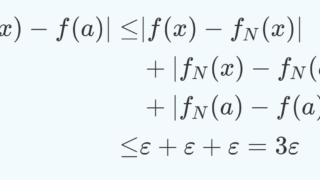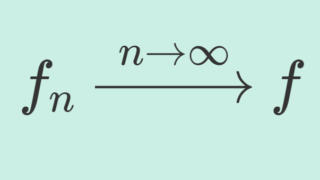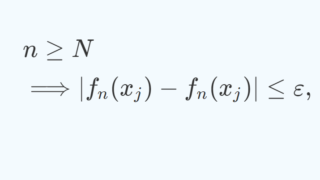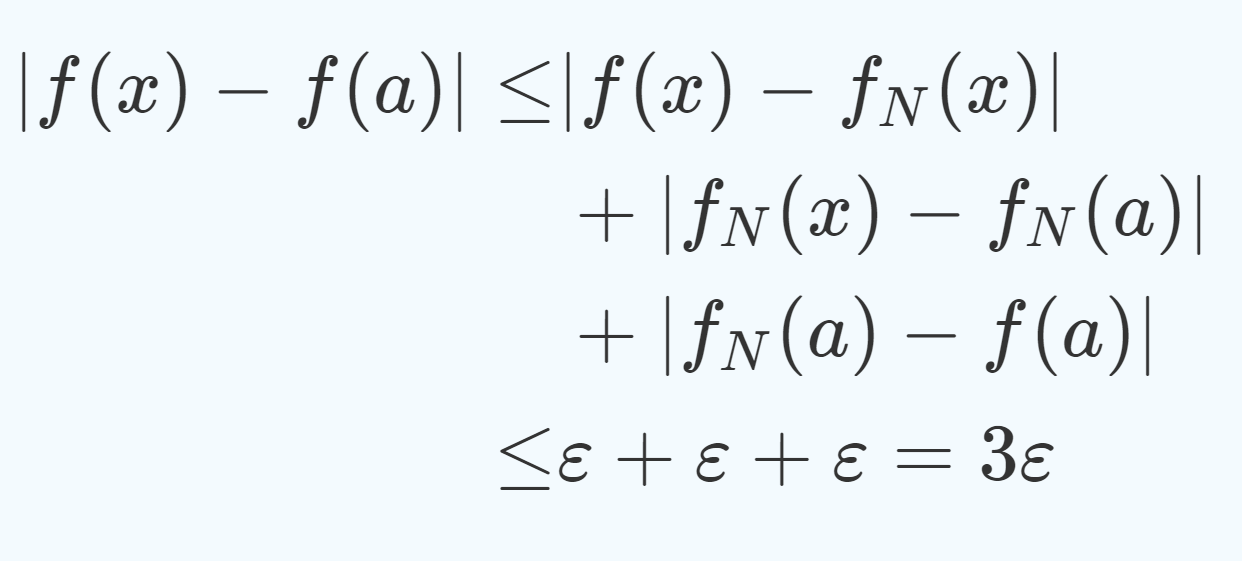数列の収束は1種類しかなかったのに,関数列の収束となると「一様収束」や「各点収束」などと,複数の収束概念が出てきて,詰まった方も多いのではないでしょうか。一様収束と各点収束を正しく理解することは,大学数学を深く理解するうえで必須の概念です。具体例とともに理解していきましょう。
一様収束と各点収束の定義
まずは定義を見て,違いを確認しましょう。
定義(一様収束)
関数列 \{f_n\} が f に A 上一様収束 (uniformly convergence) するとは,
\lim_{n\to\infty} \sup_{x \in A} |f_n(x) - f(x) | = 0
が成立すること。すなわち,
任意の \varepsilon > 0 に対して,ある N \ge 1 が存在して,任意の x \in A に対して,
が成立することを言う。
定義(各点収束)
関数列 \{f_n\} が f に A 上各点収束 (pointwise convergence) するとは,各 x \in A に対して,
\lim_{n\to\infty} f_n(x) = f(x)
が成立すること。すなわち,
任意の \varepsilon > 0 と任意の x \in A に対して,ある N \ge 1 が存在して,
が成立することを言う。
\lim を用いた形と, \varepsilon– \delta 論法を用いた形の両方で述べてみました。一様収束と各点収束の定義を比較すると,以下のようなことに気づくでしょう。
- 一様収束は \sup_{x\in A} としてから極限をとっているが,各点収束は x \in A を一つだけ固定して極限をとっている
- 一様収束は, N は \varepsilon のみに依存するが,各点収束では N は \varepsilon,x に依存する。
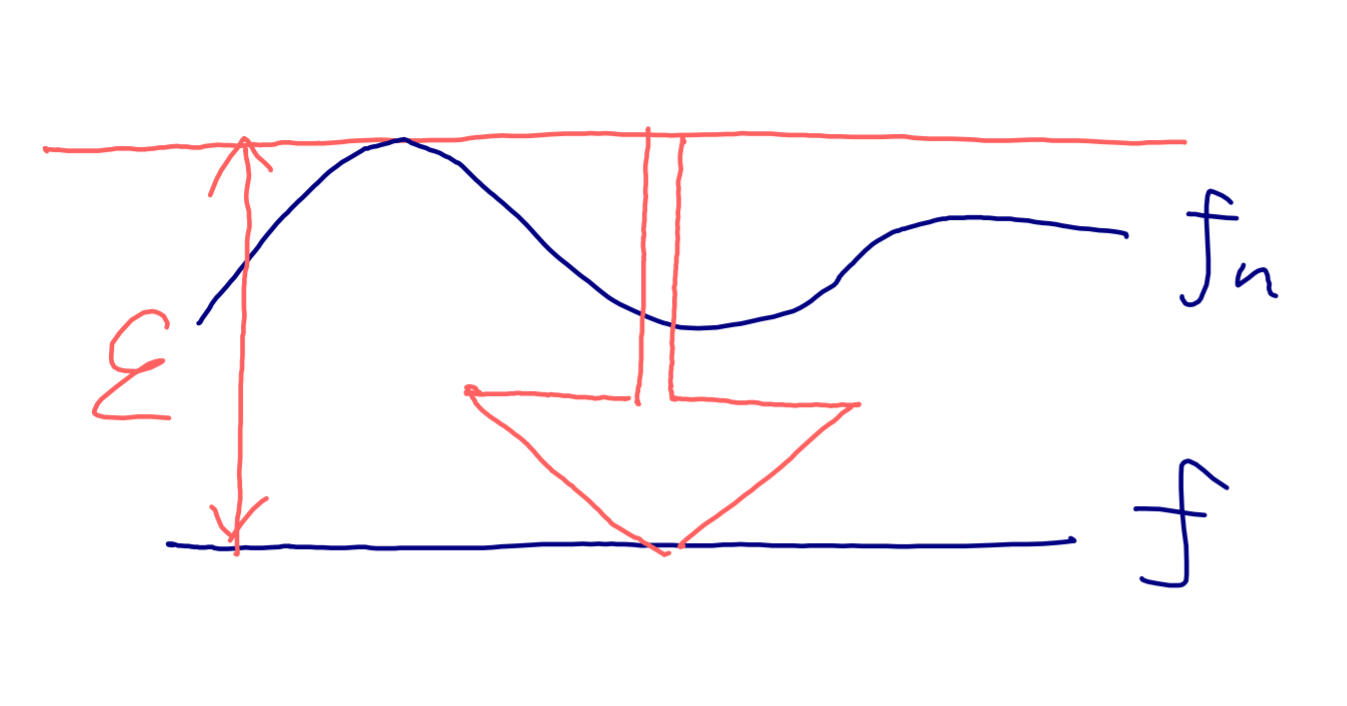
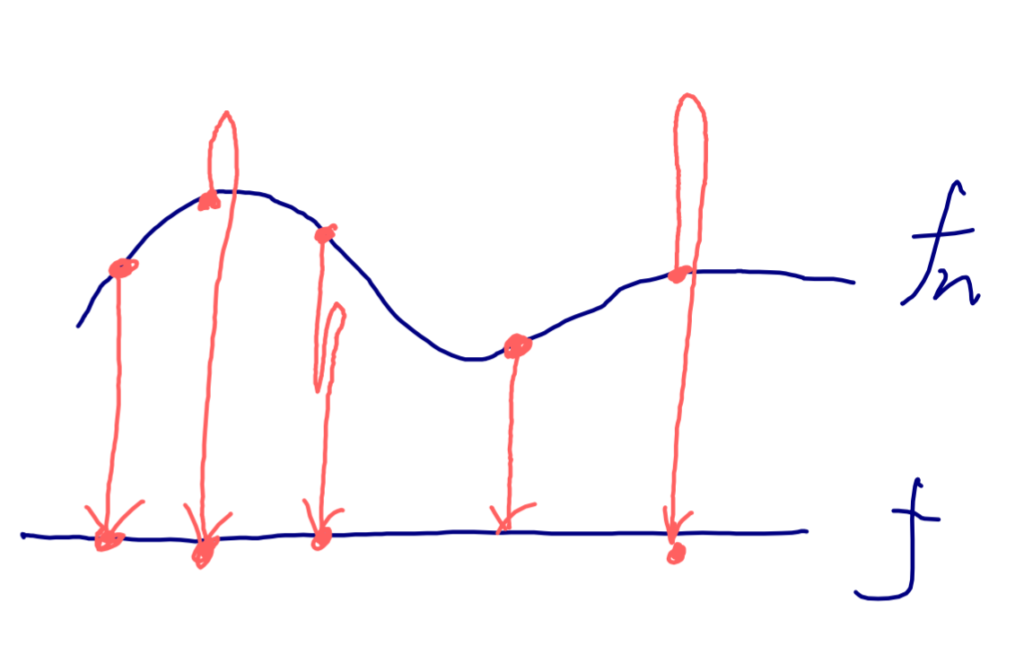
一様収束とは「関数列全体がまんべんなく収束する」ことを表し,各点収束とは「各 x \in A を止めて \{f_n(x) \} を単に数列とみてから数列の極限として考えた収束」を表します。図を用いてまとめてみましょう。
- 一様収束とは,関数列全体がまんべんなく収束することを表す。
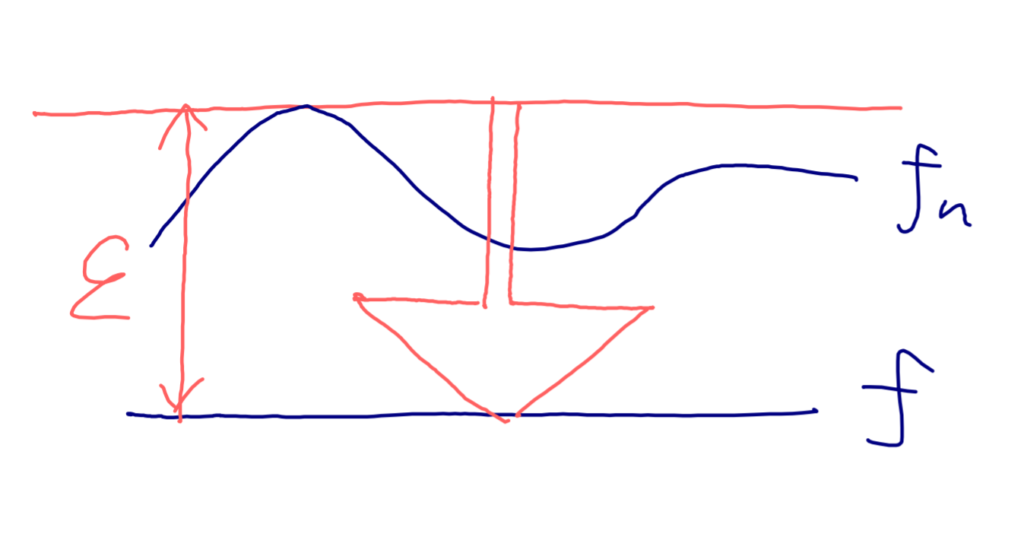
- 各点収束とは,各点ごとに考えて収束することを表す。
また,定義明らかに次の定理が成立します。
定理(一様収束 \Rightarrow 各点収束)
関数列 \{f_n\} が f に一様収束するとき, \{f_n\} は f に各点収束する。
一様収束のほうが各点収束より強い概念であるということです。各点収束しても,一様収束しない例があります。以下では,一様収束する例,各点収束するが一様収束しない例をそれぞれ確認してみましょう。
一様収束と各点収束の具体例
一様収束も各点収束もする例
例1.
\textcolor{red}{f_n(x) = x^n, \, f(x) = 0}
とおくと, \{f_n\} は [0, 1/2] 上 f に一様収束する。
実際,
\sup_{x \in [0, 1/2]} |x^n - 0| = {\left(\frac{1}{2}\right)}^n \xrightarrow{n\to\infty} 0
のため,確かにこれは一様収束します。よって各点収束もします。
例2.
\textcolor{red}{ f_n(x) = \frac{1}{n+x}, \, f(x) = 0}
とおくと, \{f_n\} は [0, \infty) 上 f に一様収束する。
これも
\sup_{x \in [0, \infty)} \left|\frac{1}{x+n} - 0 \right| = \frac{1}{n} \xrightarrow{n\to\infty} 0
のため,一様収束します。よって各点収束もします。
各点収束するが,一様収束しない例
例3.
\textcolor{red}{ f_n(x) = x^n, \, f(x) = \begin{cases} 0 & 0 \ge x < 1\\ 1 & x=1 \end{cases}}
とおくと, \{f_n\} は [0, 1] 上 f に各点収束するが一様収束しない。
例1と定義域のみ違うことに注意してください。実際,この関数は
\sup_{x \in [0, 1]} |f_n(x) - f(x) | =1 \xrightarrow{n\to\infty} 1
なので,一様収束しません。「全体がまんべんなく収束する」訳ではないということですね。
例4.
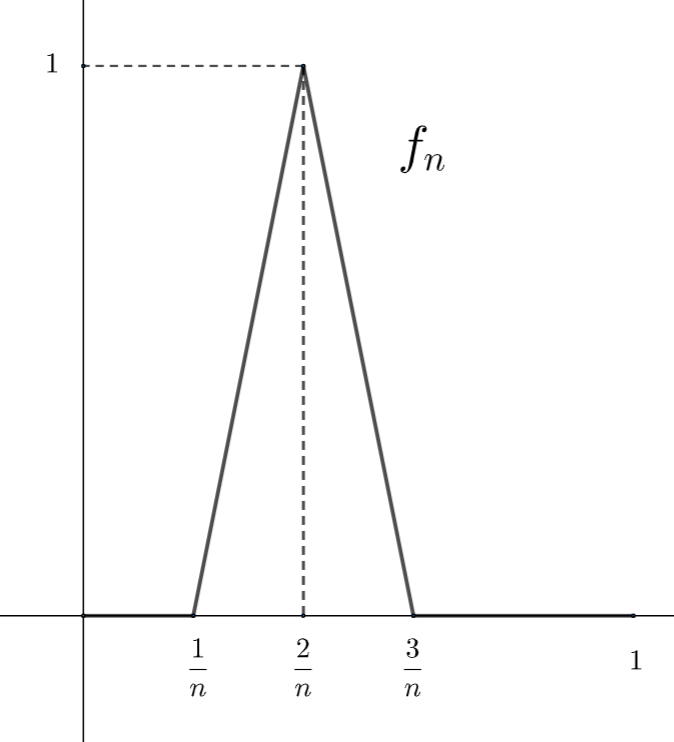
\{f_n\} を以下のように定め, f(x) = 0 とする。
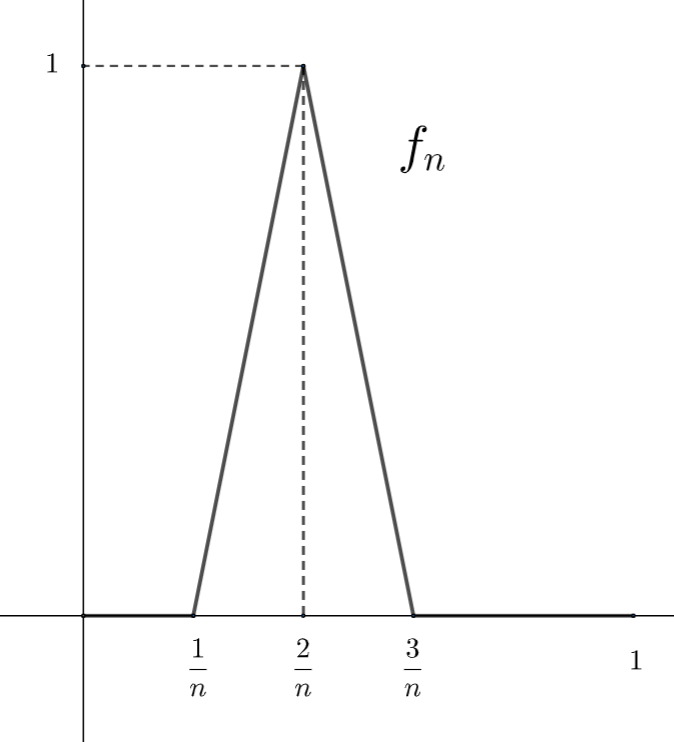
このとき, \{f_n\} は [0, 1] 上 f に各点収束するが一様収束しない。
実際,任意の x\in (0, 1] について,n を十分大きくとると 3/n < x であり,このとき, f_n(x) = 0 = f(x) となります。このことと f_n(0) = 0 = f(0) \, (n\ge 1) より,各点収束します。一方で,
\sup_{x \in [0,1]} |f_n(x) - 0 | = 1 \xrightarrow{n\to\infty} 1
であるため,一様収束しません。これも「全体がまんべんなく収束する」訳ではないということですね。
一様収束のメリット
ここまで,一様収束と各点収束の違いを確認しました。それでは,なぜ一様収束を考えるのでしょうか。一様収束のメリットはたとえば以下のようなものが挙げられます。
- 連続関数列の一様収束極限は必ず連続関数になる。
- 積分と極限が交換可能。
前者については別記事で解説しているので,以下のリンク先を参照してください!
数学にまつわる様々な計算をする際に扱いやすい,ということですね。
広義一様収束
定義域を任意の有界閉区間(有界閉集合)に制限したとき,それが一様収束することを広義一様収束する (converge uniformly on compacts) といいます。詳しくは,以下の記事を参照してください。
おまけ ~各点収束から一様収束が従う定理~
通常は,各点収束は一様収束より弱い概念のため,各点収束から一様収束は従いませんが,条件を追加すれば各点収束から一様収束を導くことができます。以下の記事で解説しているので,ぜひ見てみてください!