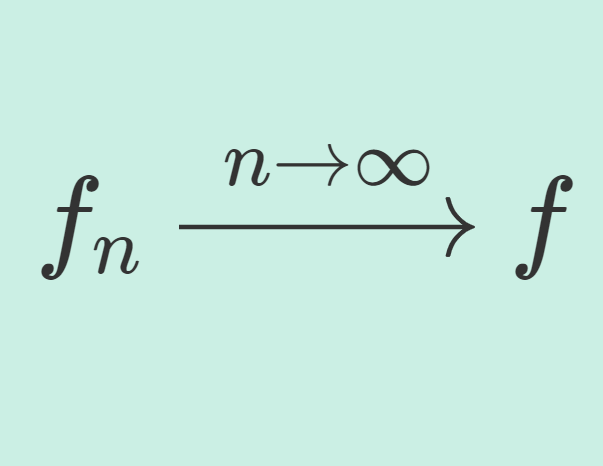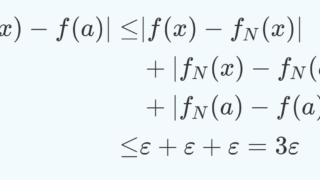関数列において広義一様収束(コンパクト一様収束)は，一様収束より広い概念です。これの定義と具体例を確認しましょう。
広義一様収束の定義
定義（広義一様収束）
I \in \mathbb{R} を区間とする(有界でなくてもよい)。
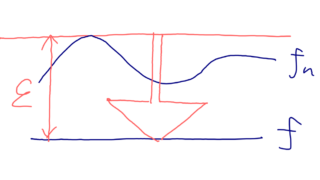
関数列 \{f_n \colon I \to \mathbb{R} \} が f\colon \mathbb{R} \to \mathbb{R} に広義一様収束する (converge uniformly on compacts) とは，任意の有界閉区間上で一様収束することである。
すなわち，任意の有界閉区間 [a, b ] \in I に対し， [a, b ] 上 f_n \xrightarrow{n\to\infty} f が一様収束となることである。
定義域全体ではなく，有界閉区間に制限したときに，一様収束が成立するとき，広義一様収束というんですね。「有界」であることと「閉区間」であることの両方が大切です。
なお，一様収束の定義自体は以下で解説しているので，参照してください。
定義から明らかに以下が成り立ちます。
定理（一様収束 \implies 広義一様収束）
f_n \xrightarrow{n\to\infty} f が一様収束であれば，これは広義一様収束である。
広義一様収束の方が一様収束より広い概念ということですね。
また，一様収束のときと同様に，以下も成立します。
定理（連続関数の広義一様収束先は連続関数）
\{f_n\} を連続な関数列とし，広義一様収束の意味で f_n \to f \,\,(n\to\infty) が成立するとする。
このとき，f は連続である。
関数の「連続」という性質は局所的なものであるため，定義域全てを考えなくても，見たい点の近くだけ考えればよいです。近くだけ考えれば，そこでは一様収束であるため，「連続関数の一様収束先は連続関数」であることから従います。
連続関数の一様収束先は連続関数であることの証明は以下の記事を参照してください。
広義一様収束の具体例
「広義一様収束するが一様収束しない例」と「一様収束する(従って広義一様収束もする)例」それぞれを挙げましょう。
広義一様収束するが一様収束しない例
例1.
\color{red} f_n(x) = x^n, \, f(x) = 0 とすると， \{f_n\} は \color{red} (-1, 1) 上広義一様収束するが，一様収束はしない。
実際， 0 < a < 1, 0 < b < 1 とすると， [-a, b] \subset (-1, 1) 上では，
\begin{aligned} \sup_{-a\le x \le b} |x^n| &= \max\{a, b\}^n \xrightarrow{n\to\infty} 0 \end{aligned}
であるから，この上で一様収束しますが，
なので， (-1, 1) 上では一様収束しません。
よって， (-1, 1) 上で広義一様収束しますが，一様収束しません。
例2.
\color{red} f_n(x) = 1_{(n, n+1)}(x), \, f(x) = 0 とする(ただし， 1_{\cdot} は定義関数)。 \{f_n\} は \color{red} [0, \infty) 上広義一様収束するが，一様収束はしない。
実際， [a, b] \subset [0, \infty) とすると，この上では，
\begin{aligned} \sup_{a\le x \le b} |1_{(n, n+1)}(x)| \xrightarrow{n\to\infty} 0 \end{aligned}
なので， [a, b 上一様収束しますが，
であるため， [0, \infty) 上では一様収束しません。
よって， [0, \infty) 上で広義一様収束しますが，一様収束しません。
一様収束する(従って広義一様収束もする)例
例3.
\color{red}{ f_n(x) = \frac{1}{n+x}, \, f(x) = 0}
とおくと， \{f_n\} は \color{red} [0, \infty) 上 f に一様収束する。
これは
\sup_{x \in [0, \infty)} \left|\frac{1}{x+n}\right| = \frac{1}{n} \xrightarrow{n\to\infty} 0
のため，一様収束します。よって当然，広義一様収束もします。
より一般の場合の広義一様収束の定義
最後に位相空間論の言葉を用いて，より一般的な広義一様収束の定義を述べましょう。
定義（広義一様収束）
X を位相空間， Y を距離空間とする。
f_n,f\colon X \to Y としたとき， f_n \xrightarrow{n\to\infty} f が広義一様収束する (converge uniformly on compacts) とは，任意のコンパクト部分集合 K \subset X 上で f_n \xrightarrow{n\to\infty} f が一様収束であることをいう。
定義域の制限が「有界閉区間」ではなく，「コンパクト」になりました。
日本語ではよく「広義一様収束」と言われますが，英語では「converge uniformly on compacts」と言ったりします。これは，直訳すると「任意のコンパクト集合上一様収束する」という意味です。
