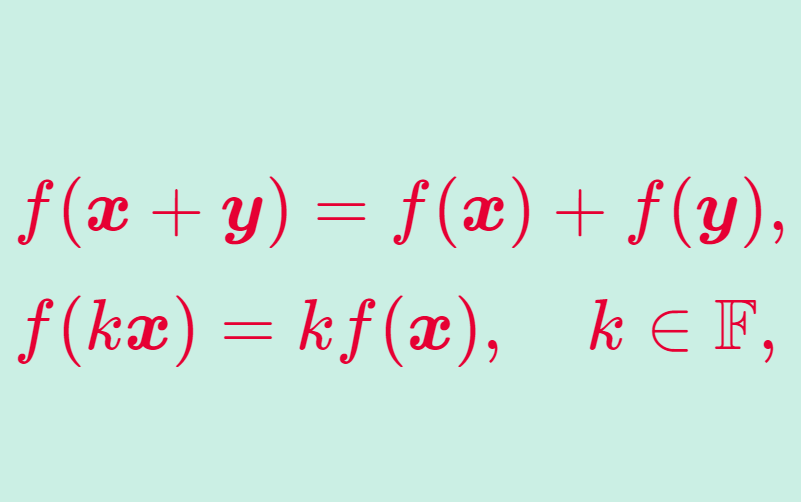行列は線形写像と呼ばれる写像を表現するのによく用いられます。そのため,行列の演算は線形写像同士の演算と対応するように定められています(本記事では線形写像が何か分からなくても構いません)。
代表的な3つの演算である「和・定数倍・積」について見ていきましょう。特に積については難しいため,図解を交えながら解説します。
行列の和
まずは行列同士の「和」を定義しましょう。
和の定義
定義(行列の和)
A=(a_{ij}), B=(b_{ij}) をともに \color{red} m \times n 行列とする。このとき, この行列の和 (sum)
\color{red} C = A + B , \,\, C = (c_{ij}) を,
で定義する。すなわち,
\color{red}\scriptsize \begin{aligned} &\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & \ldots & b_{1n} \\ b_{21} & b_{22} & \ldots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn} \end{pmatrix} \\ &= \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12}& \ldots & a_{1n}+ b_{1n} \\ a_{21}+ b_{21} & a_{22}+ b_{22} & \ldots & a_{2n}+ b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+ b_{m1} & a_{m2}+ b_{m2} & \ldots & a_{mn}+ b_{mn} \end{pmatrix}\end{aligned}と定義する。
スマホで表示してもきれいになるよう,行列の文字サイズを小さくしています。
ポイントは以下の2つです。
- 行列の和は同じ形( m\times n )の行列に対して定義され,同じ形の行列が得られること。
- 行列の和は各成分ごとの和であること。
- 行列の和は線形写像の和 f + g に対応している。
和の具体例
少しだけ例を挙げます。
行列の和の具体例
- \begin{pmatrix} 1\\ 5 \end{pmatrix} +\begin{pmatrix} 1\\ 2 \end{pmatrix} = \begin{pmatrix} 2\\ 7 \end{pmatrix}.
- \begin{pmatrix} 1& 2\\ 3 & 4 \end{pmatrix} + \begin{pmatrix} 2& 3\\ 4 & 5 \end{pmatrix} = \begin{pmatrix} 3& 5\\ 7 & 9 \end{pmatrix}.
行列の定数倍
定数倍の定義
定義(行列の定数倍)
A=(a_{ij}) を \color{red}m \times n 行列, k を定数とする。このとき, この行列の定数倍 (constant times)
\color{red} B = kA, \,\, B = (b_{ij}) を,
で定義する。すなわち,
\color{red}\small \begin{aligned} &k\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} \\ &= \begin{pmatrix} ka_{11} & ka_{12} & \ldots & ka_{1n} \\ ka_{21} & ka_{22} & \ldots & ka_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ ka_{m1} & ka_{m2} & \ldots & ka_{mn} \end{pmatrix} \end{aligned}と定義する。
ポイントは以下の2つです。
- 行列の定数倍は各成分ごとの定数倍であること。
- 行列の定数倍は線形写像の定数倍 kf に対応している。
また,同じ形の行列に対し,行列の差 (difference) を \color{red} A - B = A + (-1) B で定義します。
定数倍の具体例
行列の定数倍の具体例
- 2\begin{pmatrix} 1& 3 \end{pmatrix} =\begin{pmatrix} 2 & 6 \end{pmatrix}.
- -3 \begin{pmatrix} 1& 2\\ 3 & 4 \end{pmatrix} = \begin{pmatrix} -3& -6\\ -9 & -12 \end{pmatrix}.
行列の積
積の定義は少し難しいので,ゆっくり理解しましょう。
積の定義
定義(行列の積)
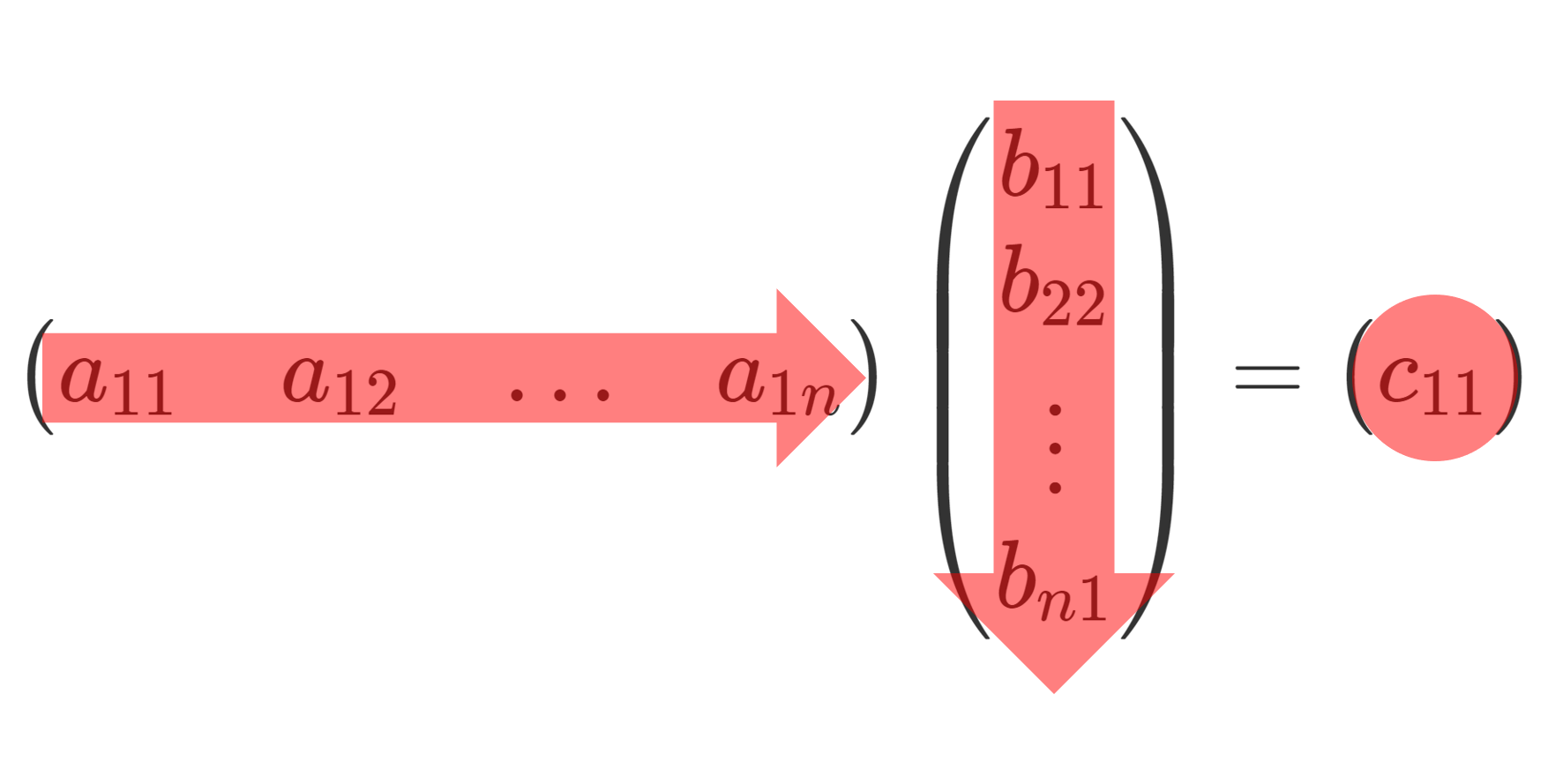
A=(a_{ij}) を \color{red} m \times n 行列, B=(b_{ij}) を \color{red}n\times l 行列とする。このとき, この行列の積 (product)
\color{red} C = AB , \,\, C = (c_{ij}) を,
で定義する。このとき, C は \color{red}m \times l 行列となる。すなわち,
\color{red}\scriptsize \begin{aligned} &\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} \begin{pmatrix} b_{11} & b_{12} & \ldots & b_{1l} \\ b_{21} & b_{22} & \ldots & b_{2l} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \ldots & b_{nl} \end{pmatrix} \\ &= \begin{pmatrix} \sum_{k=1}^n a_{1k}b_{k1} & \sum_{k=1}^n a_{1k}b_{k2}& \ldots & \sum_{k=1}^n a_{1k}b_{kl} \\ \sum_{k=1}^n a_{2k}b_{k1} & \sum_{k=1}^n a_{2k}b_{k2} & \ldots & \sum_{k=1}^n a_{2k}b_{kl} \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{k=1}^n a_{mk}b_{k1} & \sum_{k=1}^n a_{mk}b_{k2} & \ldots & \sum_{k=1}^n a_{mk}b_{kl} \end{pmatrix}\end{aligned}と定義する。
上で, A, B は違う形の行列ですが,成分表示した上の表現では,同じ形のように見えてしまっていることに注意しましょう。
定義が少し難しいですが,まずはポイントを確認しましょう。
- 行列の積は \textcolor{blue}{m} \times \textcolor{red}{n} と \textcolor{red}{n} \times \textcolor{green}{l} に対して定義できて, \textcolor{blue}{m} \times \textcolor{green}{l} の行列を返す。特に,左の行列の列の数 n と右の行列の行の数 n が一致していなければならない。
- 行列の積は線形写像の合成 f \circ g に対応している。
行列の積の定義は変ですが,線形写像の合成と対応しているため,わざと難解な定義になっています。
補足ですが, A を n \times n 行列とするとき, \color{red} A A のことを \color{red} A^2 とも表します。 n 乗も同様です(行列の n 乗)。
行列の積を完全にマスターしよう
行列の積は難しいので,少しずつ理解しましょう。図解も交えて解説します。
まず, 1 \times n 行列と n \times 1 行列の積を考えてみます。
1つ目の行列は右から左に,2つ目の行列は上から下に進んで組み合わせをつくり,和をとっていますね。
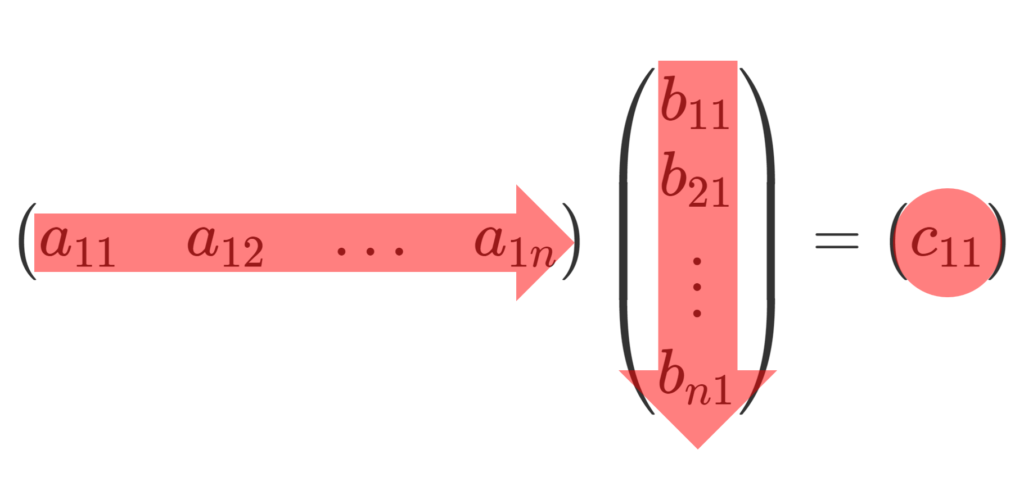
この状態で,1つ目の行列を縦に拡張すると,計算後の行列も縦に拡張されます。
\begin{gathered} \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} \begin{pmatrix} b_{11} \\ b_{21} \\ \vdots \\ b_{n1} \end{pmatrix} = \begin{pmatrix} c_{11} \\ \vdots \\ c_{i1} \\ \vdots \\ c_{m1} \end{pmatrix}, \\ \begin{aligned} c_{i1} &= \sum_{k=1}^n a_{ik} b_{k1} \\ & = a_{i1} b_{11} + a_{i2}b_{21} + \cdots + a_{in}b_{n1} \end{aligned} \end{gathered}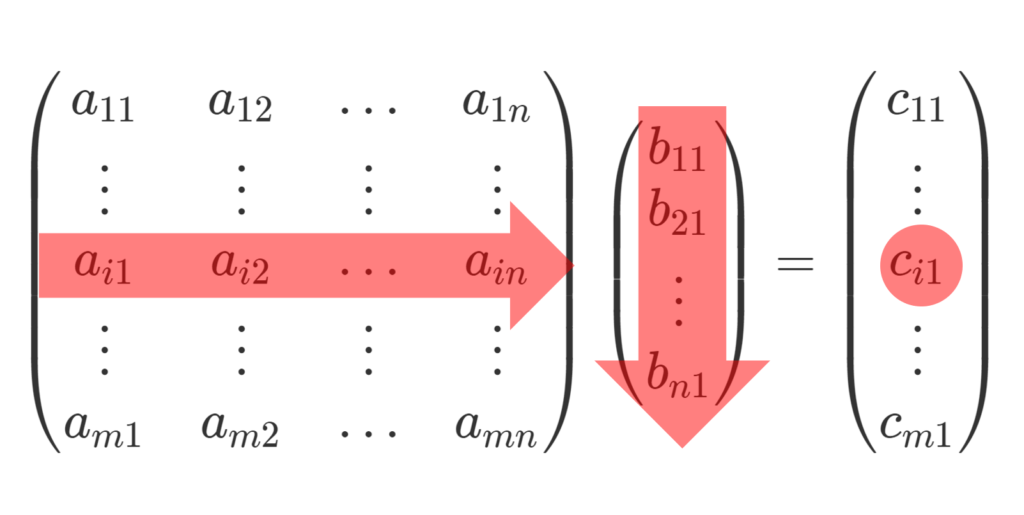
さらにこの状態で,2つ目の行列を横に拡張すると,計算後の行列も横に拡張されます。
\small \begin{gathered} \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \ldots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} \begin{pmatrix} b_{11} &\ldots & b_{1j} &\ldots & b_{1l} \\ b_{21}&\ldots & b_{2j} &\ldots & b_{2l} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n1} &\ldots & b_{nj} &\ldots & b_{nl} \end{pmatrix} \\ = \begin{pmatrix} c_{11}& \ldots & c_{1j}& \ldots& c_{1l} \\ \vdots & \vdots & \vdots & \vdots & \vdots\\ c_{i1}& \ldots& c_{ij} &\ldots &c_{il}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ c_{m1}& \ldots &c_{mj} &\ldots &c_{ml} \end{pmatrix}, \\ \begin{aligned} c_{ij} &= \sum_{k=1}^n a_{ik} b_{kj} \\ & = a_{i1} b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} \end{aligned} \end{gathered}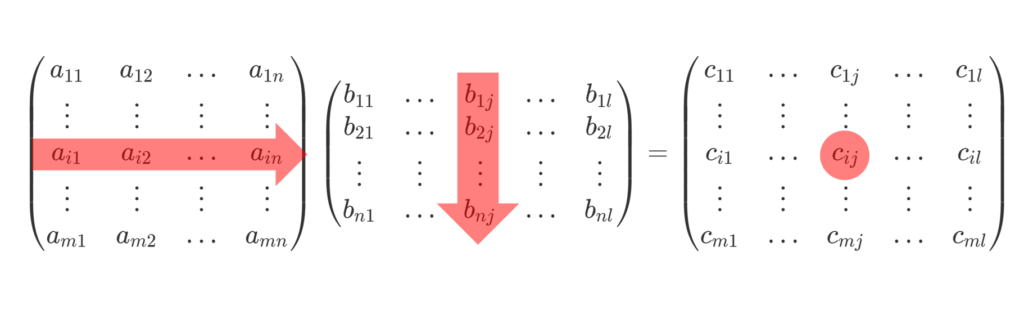
行列の積のイメージが少しでも沸いていれば幸いです。
積の具体例
行列の積の具体例を挙げましょう。
行列の積の具体例1.
- \begin{pmatrix} 1 & 2 \end{pmatrix} \begin{pmatrix} 1 \\ 3 \end{pmatrix} = \begin{pmatrix} 1\cdot 1 + 2 \cdot 3 \end{pmatrix} = \begin{pmatrix} 7 \end{pmatrix} .
- \begin{pmatrix} 1 \\ 2 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} = \begin{pmatrix}1 & 2 & 3 \\ 2 & 4 & 6 \end{pmatrix} .
- \begin{pmatrix} 1 & 2 \\ 3 & 4\end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0& 1 \end{pmatrix} = \begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix} .
行列の積の具体例2.
A = \begin{pmatrix} 1 & 2 \\ 3& 4\end{pmatrix}, B = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} とすると,
\begin{gathered} AB = \begin{pmatrix} 5 & 4 \\ 11 & 10 \end{pmatrix}, \\ BA = \begin{pmatrix} 7 & 10 \\ 5 & 8 \end{pmatrix} \end{gathered}となる。
実際に計算して確認してみましょう。
行列の積の注意点~AB ≠ BA~
先ほどの具体例2.を見てください。 A, B はともに 2 \times 2 行列だったため, AB, BA の両方が定義できました。このとき, AB \ne BA になっていますね。このように,行列においては,一般に交換法則は成立しません。これは,写像の合成が一般に f \circ g \ne g \circ f となることに対応しています。注意しましょう。
行列の演算の性質
行列の性質をいくつか紹介します。
命題(行列の演算の性質)
- A, B, C を m \times n 行列とするとき,
- (A + B) + C = A + (B + C) (結合法則),
- A + B = B + A (交換法則).
- A を m \times n 行列とし, O を同じ形の零行列とすると,
- A + O = O + A = A.
- A, B, C をそれぞれ n_1\times n_2, n_2\times n_3, n_3\times n_4 行列とすると,
- (AB)C = A(BC) (結合法則).
- A,B を m \times n , m\times l 行列, O_{m,n} O_{n, l}, O_{m,l} をそれぞれ m\times n, n \times l, m \times l 零行列とすると,
- AO_{n,l} = O_{m,l},
- O_{m,n} B = O_{m,l}.
- A を n 次正方行列, I を n 次単位行列とするとき,
- AI = IA = A .
なお,正方行列において積の交換法則 AB = BA が一般に成立しないことは,先ほど注意喚起したとおりです。
証明はほぼ自明なので省略しますが,分からない場合はよく考えてみましょう。
行列の成分ごとの積
和・定数倍の計算は行列の各成分ごとの計算でした。一方で,積はそうではありませんでした。これは,不思議に思ったかもしれません。数学においては,あまり一般的には使われないかもしれませんが,積にも成分ごとの積が存在します。これを,アダマール積 (Hadamard product) といい, \color{red} A \odot B や \color{red} A \circ B などと書きます。詳しくは,以下を参照してください。
行列と線形写像の関係
行列は,線形写像の表示として使われる,と何度か解説の中で述べました。これについて,線形写像の知識がある場合は,以下の記事を見るとよいでしょう。