関数(写像)の合成について,定義・具体例・注意点・性質の順に解説します。
合成関数(合成写像)の定義
定義(関数・写像の合成)
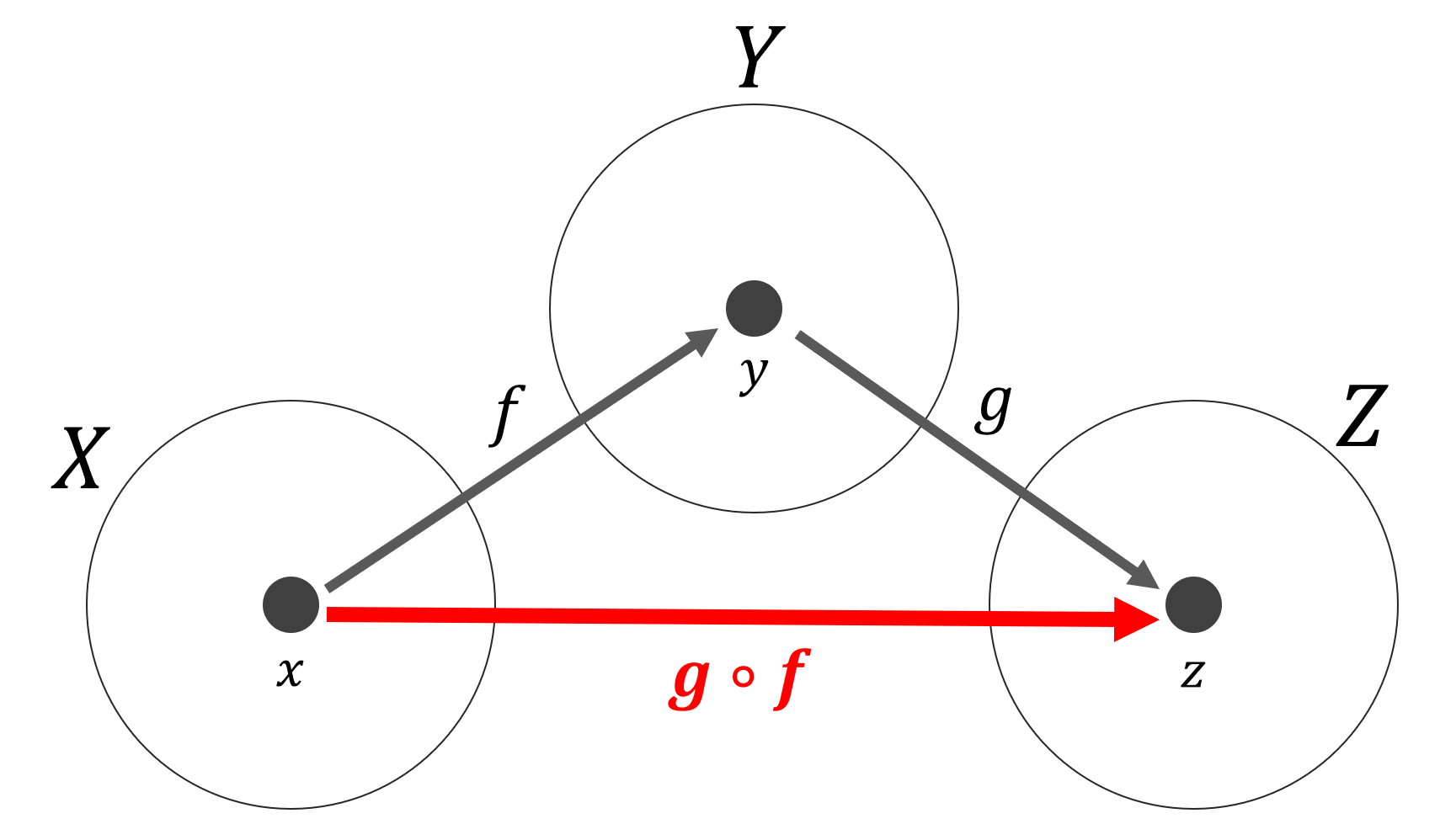
f\colon X \to Y ,\, g\colon Y \to Z とする。このとき,2つの対応 x \stackrel{f}{\longmapsto} f(x) \stackrel{g}{\longmapsto} g(f(x)) により,対応
X \ni x \longmapsto g(f(x)) \in Z
を考えることができる。この関数・写像を f と g の合成関数 (composite function)・合成写像 (composite mapping) といい,
とかく。すなわち, g \circ f (x) = g(f(x)) である。
図でイメージすると以下のようになります。
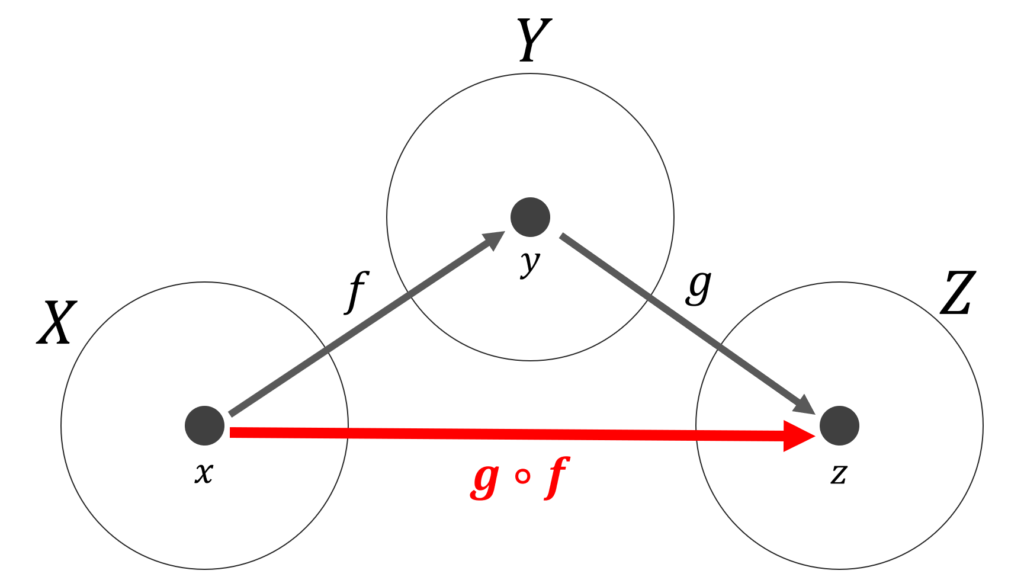
注意ですが, g \circ f とかいたとき,先に計算する(作用する)のは f からであることです。関数の合成は右から計算するということですね。
合成関数(合成写像)の具体例
簡単な具体例を挙げましょう。
関数の合成の例
f, g \colon \mathbb{R} \to \mathbb{R} を f(x) = 2x, g(x) = x^2 とする。
このとき, g \circ f, f\circ g \colon \mathbb{R} \to \mathbb{R} で,
\begin{gathered} g\circ f (x) = g(2x) = (2x)^2 = 4x^2 \\ f \circ g (x) = f(x^2) = 2 x^2 \end{gathered}
とかける。
合成関数(合成写像)の大事な注意~交換法則は成立しない~
上の例では, g \circ f (x) = 4 x^2, \, f \circ g (x) = 2 x^2 でした。一般に g \circ f と f \circ g は一致しません。これは注意しましょう。
合成関数(合成写像)の性質
以下の2番以降では,全射・単射・全単射や,逆関数(逆写像)の知識は既知とします。
命題(関数・写像の合成の性質)
以下, f\colon X \to Y ,\, g\colon Y \to Z, \, h\colon Z \to W とする。
- h \circ (g \circ f) = (h \circ g) \circ f. (結合法則)
- f,g がともに全射であるとき, g \circ f も全射である。
- f,g がともに単射であるとき, g \circ f も単射である。
- f,g がともに全単射であるとき, g \circ f も全単射である。
- 4.のとき,逆関数(逆写像)に関して, (g \circ f)^{-1} = f^{-1} \circ g^{-1} である。
- g \circ f が全射のとき, g は全射であるが f は全射とは限らない。
- g \circ f が単射のとき, f は単射であるが g は単射とは限らない。
- g \circ f が全単射のとき, f は単射かつ g は全射である。
1,5は特に大切なので覚えておくようにしましょう。
一つ一つ丁寧に証明します。
証明
1. h \circ (g \circ f) = (h \circ g) \circ f. (結合法則)
h \circ (g \circ f)(x) = h((g\circ f)(x)) = h(g(f(x))) = (h\circ g) (f(x)) = (h \circ g) \circ f(x) より。
2. f,g がともに全射であるとき, g \circ f も全射である。
f, g が全射であるから, f(X) = Y, g(Y) = Z であることに注意。ここで,
g\circ f(X) = g(f(X)) = g(Y) = Z
であるから, g\circ f も全射である。
3. f,g がともに単射であるとき, g \circ f も単射である。
f, g が単射であるから, x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2), \, y_1 \ne y_2 \Rightarrow f(y_1) \ne f(y_2) であることに注意。ここで,
\begin{aligned} x_1 \ne x_2 &\Rightarrow f(x_1) \ne f(x_2) \\ &\Rightarrow g(f(x_1)) \ne g(f(x_2)) \end{aligned}
であるから, g\circ f も単射である。
4. f,g がともに全単射であるとき, g \circ f も全単射である。
2と3より直ちに従う。
x \stackrel{f}{\longmapsto}y \stackrel{g}{\longmapsto} z5. 4.のとき,逆関数(逆写像)に関して, (g \circ f)^{-1} = f^{-1} \circ g^{-1} である。
とする。このとき,それぞれの逆関数の合成を考えると,
であるから, f^{-1} \circ g^{-1} (z) = x となる。
一方で, g \circ f (x) = z であるから, (g\circ f)^{-1} (z) = x である。
よって, f^{-1} \circ g^{-1} = (g \circ f)^{-1}.
6. g \circ f が全射のとき, g は全射であるが f は全射とは限らない。
g \circ f が全射であることと, f(X) \subset Y であることから,
Z = g\circ f (X) \subset g(Y)
より, Z = g(Y) なので, g は全射である。
一方で,以下は f が全射とは限らない例である。
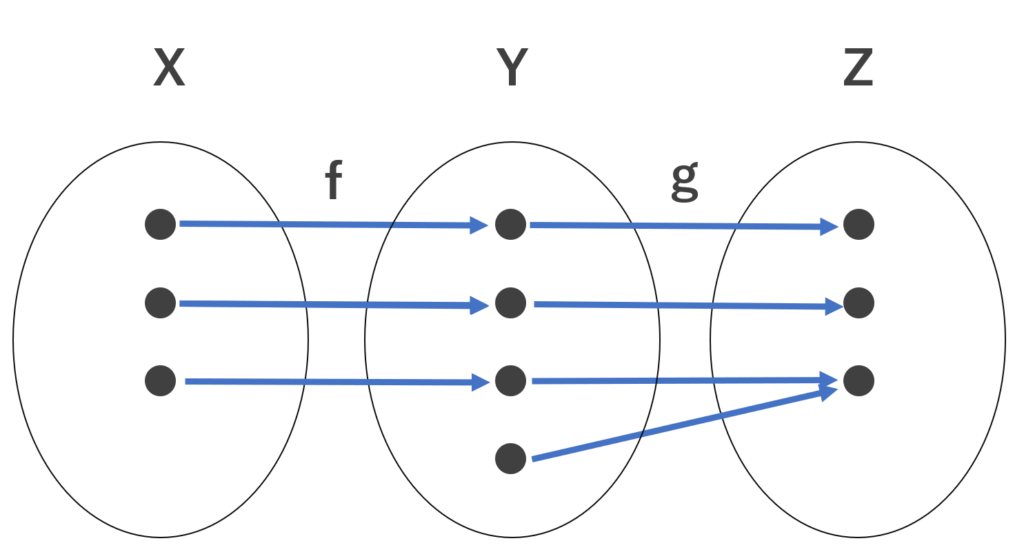
7. g \circ f が単射のとき, f は単射であるが g は単射とは限らない。
g\circ f は単射より, x_1 \ne x_2 \Rightarrow g\circ f (x_1) \ne g\circ f (x_2) であるから, f(x_1) \ne f(x_2) でなければならない。すなわち f は単射である。
一方で,以下は g が単射とは限らない例である(先程と同じ例である)。

8. g \circ f が全単射のとき, g は全射かつ f は単射である。
6と7より直ちに従う。
証明終
性質については少々難しいかもしれませんが,定義と注意についてはしっかり抑えておきましょう。