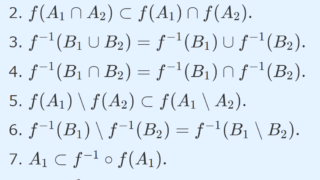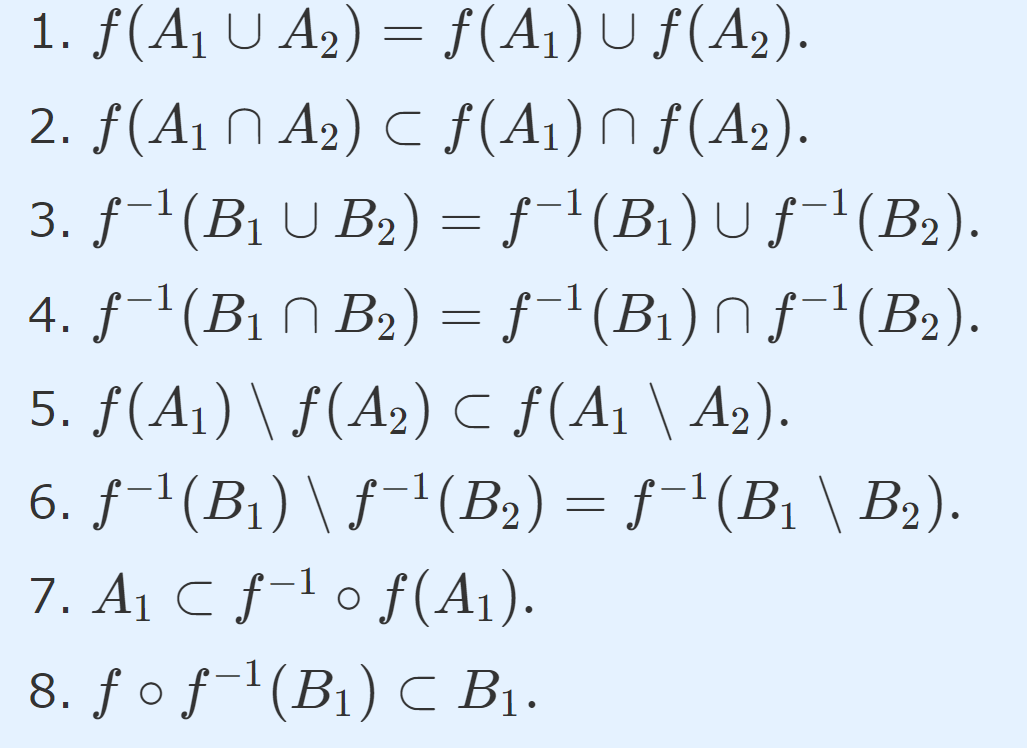写像(関数)における像・逆像を定義し,イメージ図と具体例を確認していきましょう。
像・逆像の定義
まずは定義を述べましょう。
定義(像・逆像)
f\colon X \to Y とする。
A \subset X に対し,
\textcolor{red}{f(A) = \{ f(x) \in Y \mid x \in A \}}
を f による A の像 (image) または 値域 (range) という。
B \subset Y に対し,
\textcolor{red}{f^{-1}(B) = \{ x \in X \mid f(x) \in B \}}
を f による B の逆像 (inverse image) または原像 (preimage) という。
なお, X 全体の像は f(X) の代わりに \color{red}\operatorname{Im} f と書くことがあります。
一番最初に注意ですが,逆像の f^{-1} は逆写像のそれとは異なります。逆写像は全単射でないと定義できませんが,今はそうでない,「写像」の意味ではありません。
この注意をもとに,イメージを考えてみましょう。このとき,以下のような写像を考えます。
像のイメージ
像とは A \subset X に対し,集合 \textcolor{red}{f(A) = \{ f(x) \in Y \mid x \in A \}} のことでした。これは,集合 A を f でうつした, Y 部分集合といえます。
イメージ図をみてみましょう。
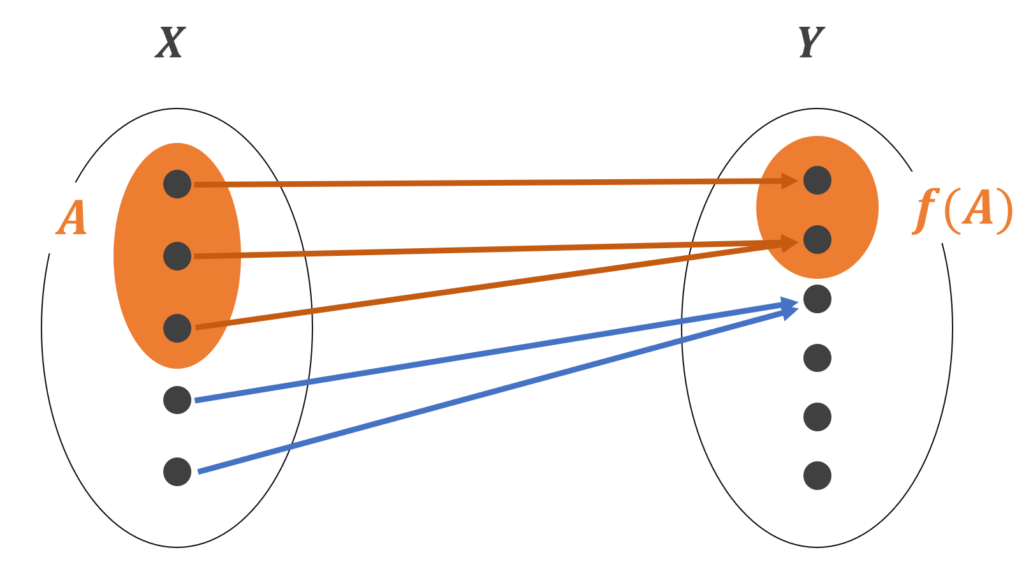
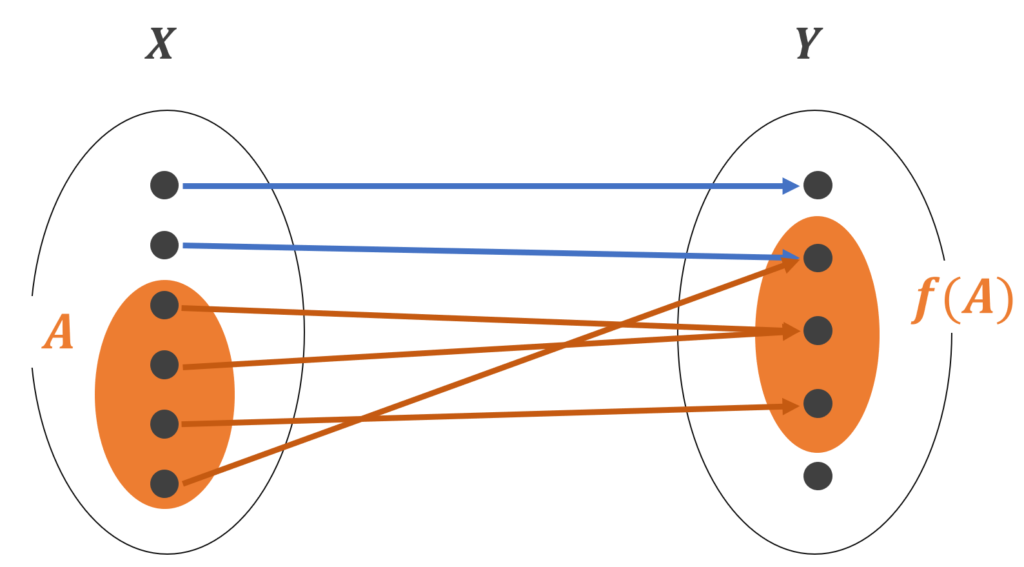
「集合 A を f でうつした, Y 部分集合」になっていますね。
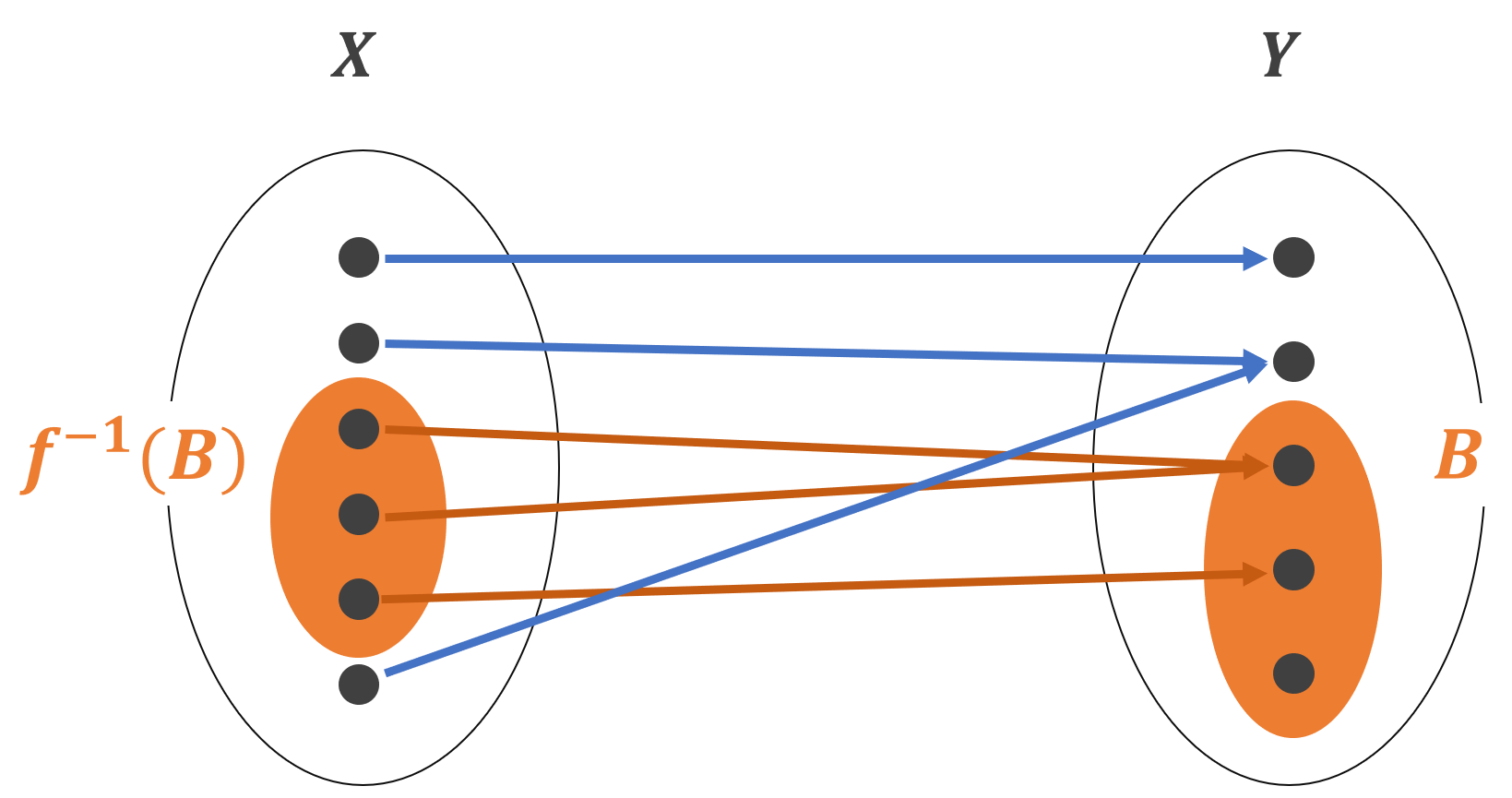
逆像のイメージ
逆像とは B \subset Y に対し,集合 \textcolor{red}{f^{-1}(B) = \{ x \in X \mid f(x) \in B \}} のことでした。これは, f でうつした先が B に入り得る X の部分集合全体といえます。
イメージ図をみてみましょう。
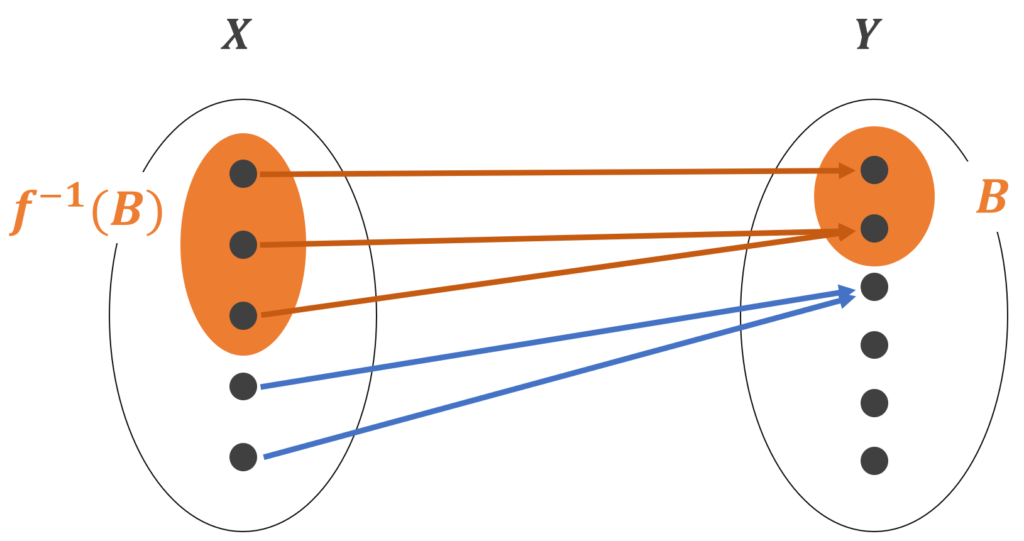
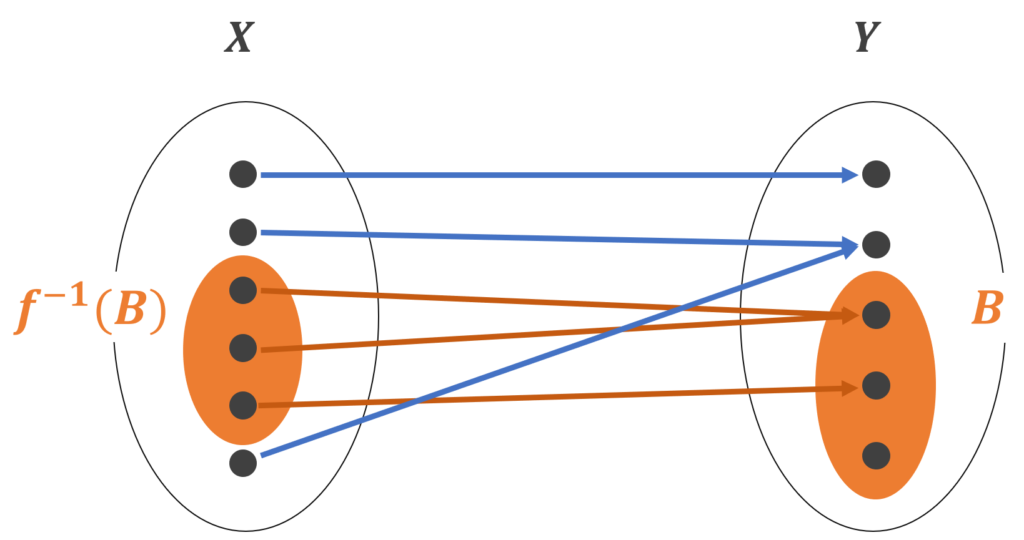
「 f でうつした先が B に入り得る X の部分集合全体」になっていますね。
ここで注意ですが, B の一番下の要素(元)は, f の行き先になっていないですが, f^{-1} (B) は考えることができますね。
像・逆像の具体例
像・逆像の具体例
f\colon \mathbb{R} \to \mathbb{R} を f(x) = x^2 とする。
このとき, f([1, 2]) = [1, 4] である。
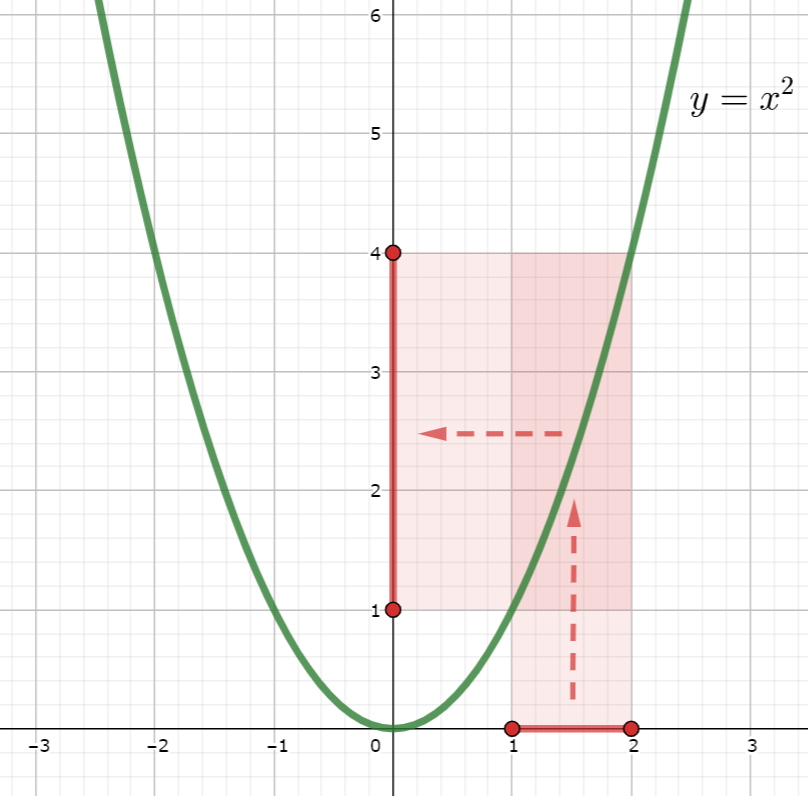
また, f^{-1} ([1, 4]) = [-2, -1] \cup [1, 2] である。
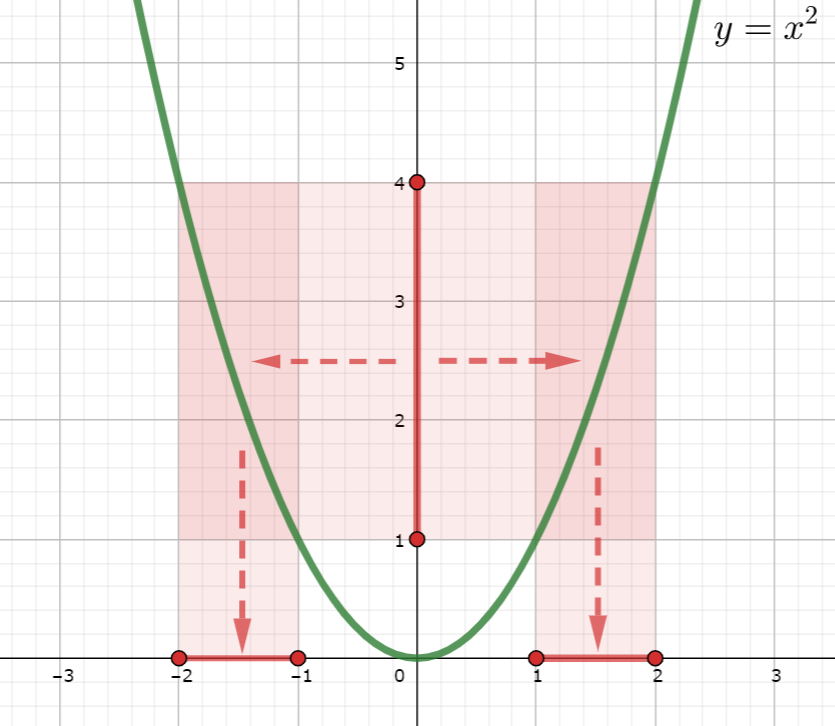
他に,たとえば
\begin{gathered} f(\{3\}) = \{9\}, \\ f(\mathbb{R}) = [0, \infty), \\ f(\varnothing) = \varnothing, \\ f^{-1}(\{2\}) = \{-\sqrt{2}, \sqrt{2}\}, \\ f^{-1}(\mathbb{R}) = \mathbb{R}, \\ f^{-1} ((-\infty, 0)) = \varnothing \end{gathered}
である。
像・逆像と集合との演算規則
像・逆像をとってから共通部分・和集合をとった集合と,逆に共通部分・和集合をとった集合に対して,像・逆像をとったものの間には,包含関係が知られています。
これについては,以下を参照してください。