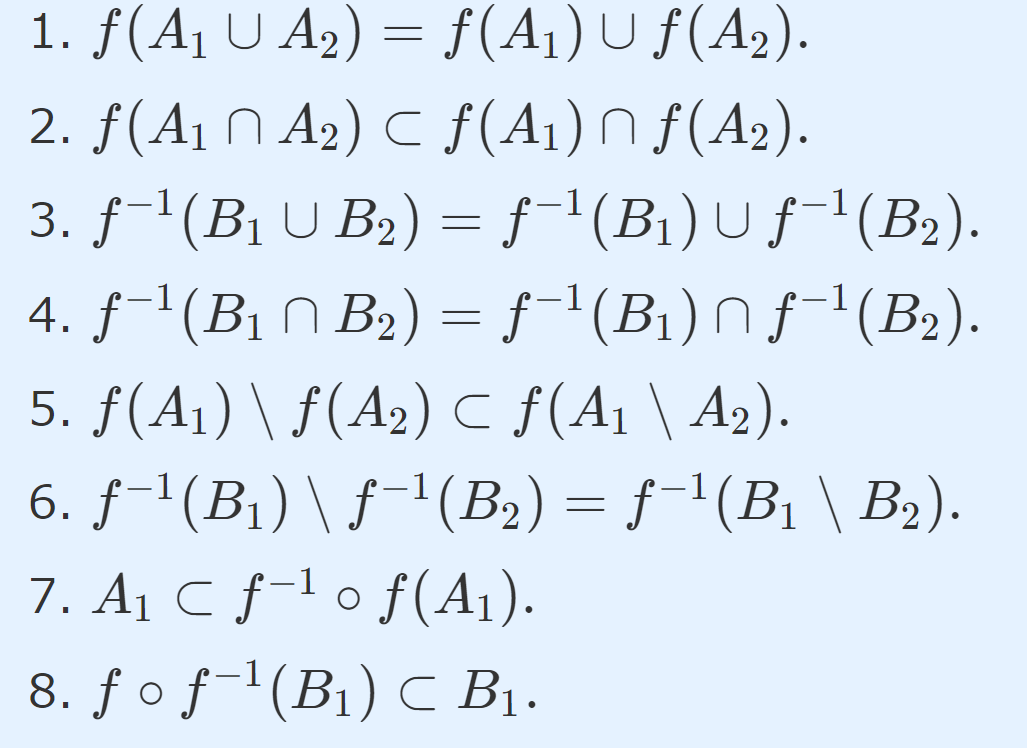像・逆像と集合との演算とその証明をします。
像・逆像と集合との演算
定理(像・逆像と集合との演算)
f\colon X \to Y を写像とし, A_1, A_2 \subset X, \quad B_1, B_2 \subset Y とする。
このとき,以下が成立する。
- f(A_1 \cup A_2) = f(A_1) \cup f(A_2).
- f(A_1 \cap A_2) \subset f(A_1) \cap f(A_2).
- f^{-1} (B_1 \cup B_2) = f^{-1} (B_1) \cup f^{-1}(B_2).
- f^{-1} (B_1 \cap B_2) = f^{-1} (B_1) \cap f^{-1}(B_2).
- f(A_1) \setminus f(A_2) \subset f(A_1 \setminus A_2).
- f^{-1}(B_1) \setminus f^{-1}(B_2) = f^{-1}(B_1 \setminus B_2) .
- A_1 \subset f^{-1} \circ f (A_1).
- f \circ f^{-1} (B_1) \subset B_1.
上の式を見ると, f より f^{-1} の方がより多くの等号が成立しているのが分かると思います。これはすなわち,像 f より逆像 f^{-1} の方が性質が良いということです。
早速証明していきましょう。
像・逆像と集合との演算の証明
集合で A = B を証明するのは A \subset B かつ B \subset A を証明するのが一般的であるので,そうしましょう。
証明に加えて,等号が成り立たないものは,その例も同時に挙げましょう。
証明
1. f(A_1 \cup A_2) = f(A_1) \cup f(A_2).
y \in f(A_1 \cup A_2) とする。このとき,ある x \in A_1 \cup A_2 が存在して, f(x) = y が成立する。
x \in A_1 とすると, y \in f(A_1) であり, x \in A_2 とすると y \in f(A_2) なので, y \in f(A_1) \cup f(A_2) である。
よって, f(A_1 \cup A_2) \subset f(A_1) \cup f(A_2) となる。
一方,y \in f(A_1) \cup f(A_2) とする。
y \in f(A_1) とすると,ある x \in A_1 が存在して, f(x) = y となる。
y \in f(A_2) とすると,ある x \in A_2 が存在して, f(x) = y となる。
結局,ある x \in A_1 \cup A_2 が存在して, f(x) =y となる。すなわち y \in f(A_1 \cup A_2 ) である。
よって,f(A_1) \cup f(A_2) \subset f(A_1 \cup A_2) となる。
2. f(A_1 \cap A_2) \subset f(A_1) \cap f(A_2).
f が単射のときは等号となる。
f(A_1\cap A_2) \subset f(A_1) かつ f(A_1\cap A_2) \subset f(A_2) であるから,
f(A_1\cap A_2) \subset f(A_1) \cap f(A_2) である。
一方で f を単射とする。 y \in f(A_1) \cap f(A_2) とすると, x_1 \in A_1, \,\, x_2 \in A_2 が存在して, f(x_1) = f(x_2) = y となる。 f は単射なので, x_1 = x_2 であり,特に x_1 \in A_1 \cap A_2 である。
これにより, y \in f(A_1 \cap A_2) が成立するため, f(A_1)\cap f(A_2) \subset f(A_1 \cap A_2) となる。
また, f(x) = x^2 に対し, f([-1, 0] \cap [0, 1]) \subsetneq f([-1, 0]) \cap f([0, 1]) であるから,一般に等号は必ずしも成立しない。
\begin{aligned} &x \in f^{-1} (B_1 \cup B_2) \\ &\Longleftrightarrow f(x) \in B_1 \cup B_2 \\ &\Longleftrightarrow f(x) \in B_1 \text{ or } f(x) \in B_2 \\ &\Longleftrightarrow x \in f^{-1} (B_1) \text{ or } x \in f^{-1} (B_2) \\ &\Longleftrightarrow x \in f^{-1}(B_1) \cup f^{-1}( B_2). \end{aligned}3. f^{-1} (B_1 \cup B_2) = f^{-1} (B_1) \cup f^{-1}(B_2).
\begin{aligned} &x \in f^{-1} (B_1 \cap B_2) \\ &\Longleftrightarrow f(x) \in B_1 \cap B_2 \\ &\Longleftrightarrow f(x) \in B_1 \text{ and } f(x) \in B_2 \\ &\Longleftrightarrow x \in f^{-1} (B_1) \text{ and } x \in f^{-1} (B_2) \\ &\Longleftrightarrow x \in f^{-1}(B_1) \cap f^{-1}( B_2). \end{aligned}4. f^{-1} (B_1 \cap B_2) = f^{-1} (B_1) \cap f^{-1}(B_2).
5. f(A_1) \setminus f(A_2) \subset f(A_1 \setminus A_2).
f が単射のときは等号となる。
y \in f(A_1) \setminus f(A_2) とする。
y \in f(A_1) より, x \in A_1 が存在して, f(x) = y となる。
y \notin f(A_2) より, x\notin A_2 である。
従って x \in A_1 \setminus A_2 であり, y \in f(A_1 \setminus A_2) となる。これより, f(A_1) \setminus f(A_2) \subset f(A_1 \setminus A_2) である。
f を単射とし, y \in f(A_1 \setminus A_2) とする。 f(x) = y となる x \in X はただ一つであり,それは x \in A_1 \setminus A_2 となる。特に, y \notin f(A_2) であり, f(A_1 \setminus A_2) \subset f(A_1) \setminus f(A_2) となる。
また, f(x) = x^2 に対し, f([-1, 1]) \setminus f([0, 1]) \subsetneq f([-1, 1] \setminus [0, 1]) であるから,一般に等号は必ずしも成立しない。
\begin{aligned} & x \in f^{-1}(B_1) \setminus f^{-1}(B_2) \\ &\Longleftrightarrow x \in f^{-1}(B_1) \text{ and } x \notin f^{-1}(B_2) \\ &\Longleftrightarrow f(x) \in B_1 \text{ and } f(x) \notin B_2 \\ &\Longleftrightarrow f(x) \in B_1 \setminus B_2 \\ &\Longleftrightarrow x \in f^{-1}(B_1 \setminus B_2). \end{aligned}6. f^{-1}(B_1) \setminus f^{-1}(B_2) = f^{-1}(B_1 \setminus B_2) .
\begin{aligned} x \in A_1 &\Longrightarrow f(x) \in f(A_1) \\ &\Longleftrightarrow x \in f^{-1} \circ f (A_1) \\ \end{aligned}7. A_1 \subset f^{-1} \circ f (A_1).
f が単射のときは等号となる。
である。特に, f が単射のときは,最初の矢印も同値になる。
また, f(x) = x^2 に対し, [0, 1] \subsetneq f^{-1} \circ f([0, 1]) であるから,一般に等号は必ずしも成立しない。
8. f \circ f^{-1} (B_1) \subset B_1.
f が全射のときは等号となる。
y \in f \circ f^{-1} (B_1) とする。このとき, x \in f^{-1}(B_1) が存在して, f(x) =y となる。
x \in f^{-1}(B_1) であるから, f(x) \in B_1 である。
すなわち, y \in B_1 であり, f \circ f^{-1} (B_1) \subset B_1 が成立する。
f を全射とすると, y\in B_1 に対し, f(x)=y となる x\in f^{-1}(B_1) が存在するため, y=f(x)\in f\circ f^{-1}(B_1) となって, B_1\subset f\circ f^{-1}(B_1) も成り立つ。
また, f(x) = x^2 に対し, f \circ f^{-1} ((-\infty , 0])\subsetneq (-\infty, 0] であるから,一般に等号は必ずしも成立しない。
より一般的な定理
先ほどは2つのみの和・共通部分を考えましたが,より一般に n 個や無限個の和・共通部分についても同様のことが成立します。
定理
- f(\bigcup_{\lambda} A_\lambda) = \bigcup_{\lambda}f(A_\lambda).
- f(\bigcap_{\lambda} A_\lambda) \subset \bigcap_{\lambda}f(A_\lambda).
- f^{-1}(\bigcup_{\lambda} A_\lambda) = \bigcup_{\lambda}f^{-1}(A_\lambda).
- f^{-1}(\bigcap_{\lambda} A_\lambda) = \bigcap_{\lambda}f^{-1}(A_\lambda).
ここで, \lambda は非可算でも構いません。証明はほぼ同様のため,省略します。