【距離空間】全有界の定義・例と有界との違いをわかりやすく

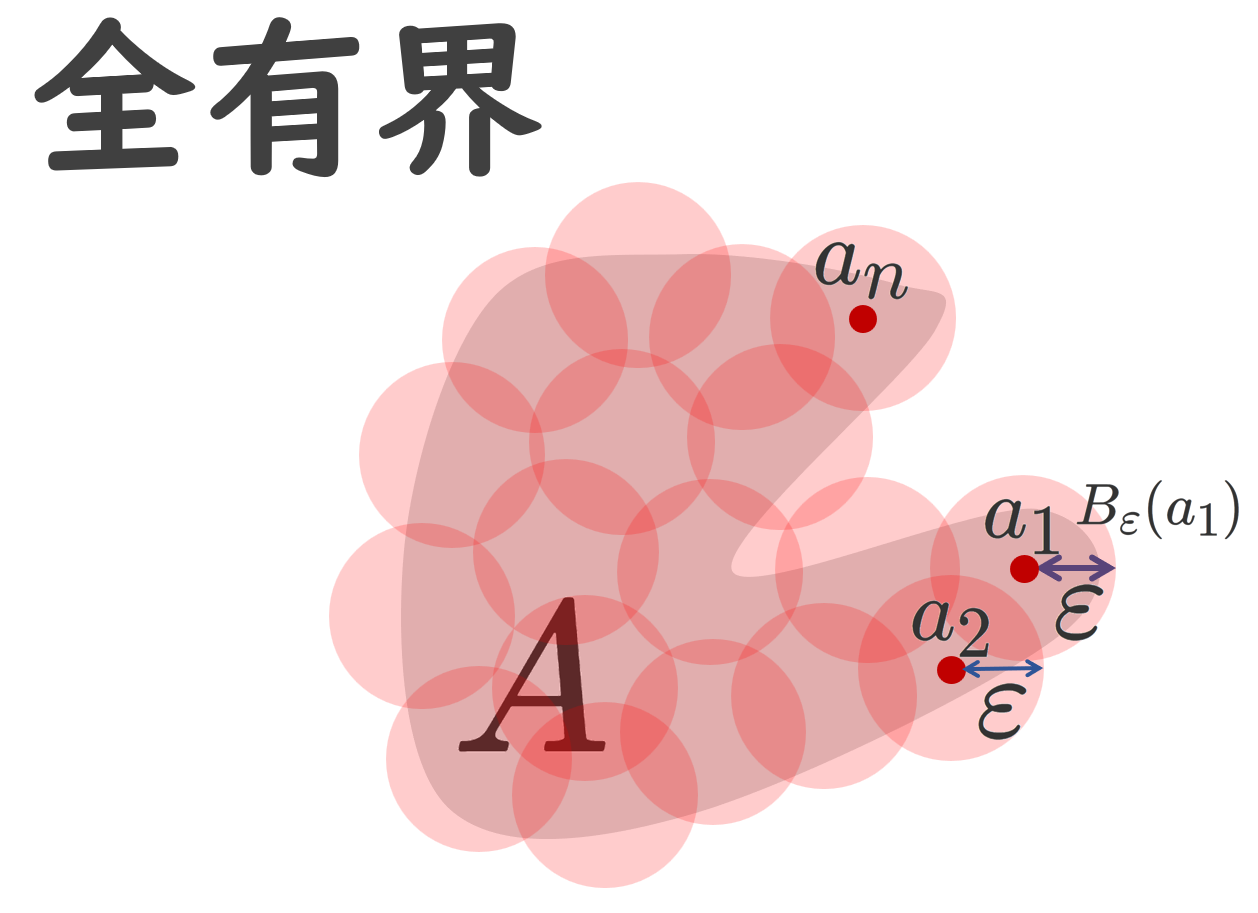
距離空間あるいはその部分集合が全有界であるとは，任意に小さい有限個の円板で，その集合全体が覆えることを言います。

距離空間における全有界性について，有界性との違いを比較しながらその定義・例を理解していきましょう。全有界であれば有界であることの証明も行います。

距離空間における有界性・全有界性
全有界ならば有界
全有界の例・そうでない例
全有界性が重要になる定理
関連する記事

距離空間における有界性・全有界性

$(X,d)$ を距離空間とし， $a\in X$ に対し， $a$ の $\varepsilon$ -近傍を

\color{red}\large B_\varepsilon (a)=\{x\in X\mid d(a,x)<\varepsilon\}

とかくことにします。簡便にするため，本記事ではこれを $a$ 中心，半径 $\varepsilon$ の円板 (disk)ということにします(広がりが平面なわけではなく，厳密には(次元が定まっていれば $d$ 次元)球体の方が適切でしょう)。

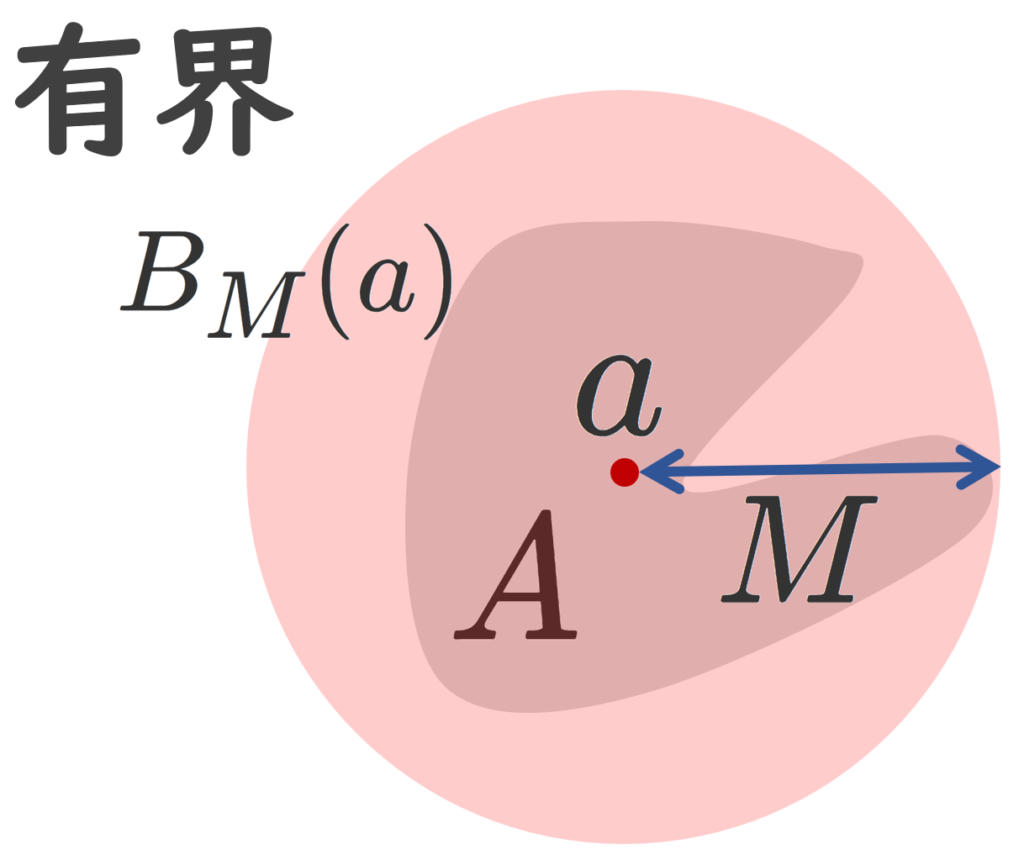
定義（有界・全有界）

$(X,d)$ を距離空間とする。

$A\subset X$ が有界 (bounded) であるとは，ある $a\in A$ と $M>0$ が存在して，

\Large\color{red} A\subset B_M(a)

とできることをいう。 $A\subset X$ が全有界 (totally bounded) であるとは，任意の $\varepsilon >0$ に対して，ある $n\ge 1$ と $a_1,a_2,\dots, a_n\in A$ が存在して，

\large \color{red}A\subset B_\varepsilon (a_1)\cup B_\varepsilon (a_2)\cup \dots\cup B_\varepsilon (a_n)

有界の定義は，ある $a\in A$ と $M>0$ が存在して， $A\subset B_M(a)$ としましたが，実際は任意の $b\in A$ に対して，ある $L>0$ が存在して， $A\subset B_L(b)$ とできます。 $L=d(a,b)+M$ とすればよいからです。

有界と全有界は，字面だけ見れば全く異なる定義ですね。

有界とは，有限距離に収まっていることを指しています。全有界とは，どんなに小さな円板でも，有限個の円板で覆えることを指します。これを有限被覆 (ゆうげんひふく; finite cover) をもつということがあります。以下の図が分かりやすいでしょう。

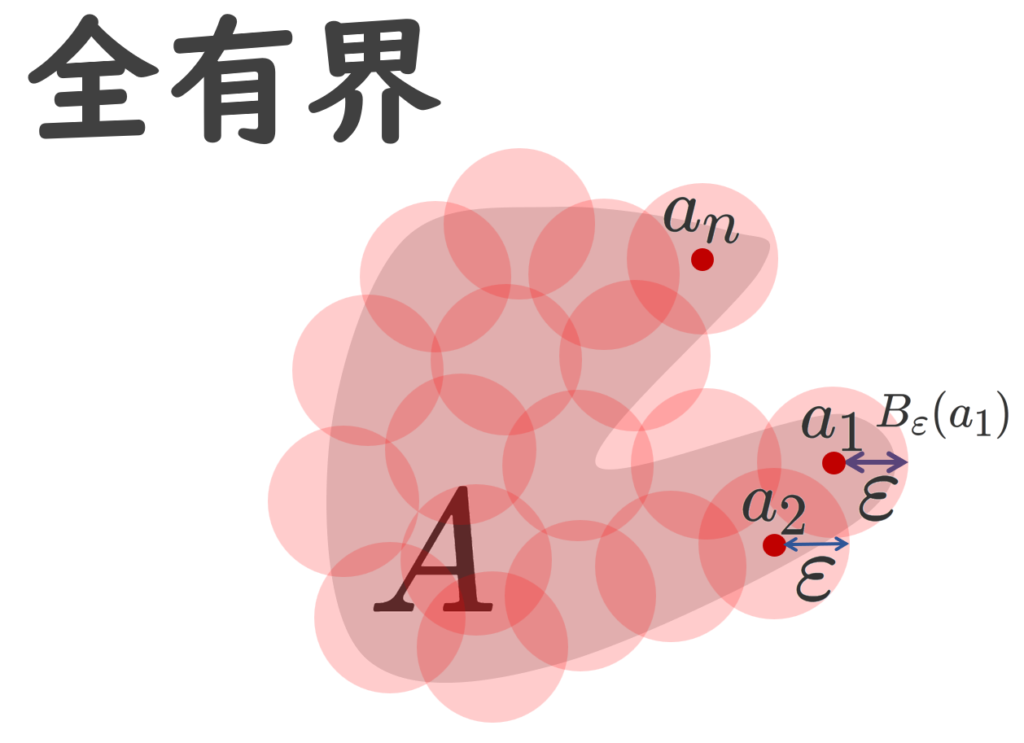
特に全有界は「任意の $\varepsilon >0$ で」であることが大切です。これを肝に銘じましょう。

全有界ならば有界

具体例を挙げる前に，定理を一つ紹介しましょう。

定理（全有界ならば有界）

$(X,d)$ を距離空間とし， $A\subset X$ とする。 $A$ が全有界であれば，有界である。

証明

$\varepsilon >0$ とする。 $A$ は全有界であるから， $a_1, a_2, \dots, a_n\in A$ が存在して， $A\subset \bigcup_{k=1}^n B_\varepsilon (a_k)$ とできる。ここで，

M= \max_{2\le k\le n} d(a_1, a_k)

とすると， $\bigcup_{k=1}^n B_\varepsilon (a_k) \subset B_{M+\varepsilon}(a_1)$ となることを示そう。 $x\in B_\varepsilon (a_k)$ とすると，

\begin{aligned} d(a_1, x)\le d(a_1, a_k)+d(a_k, x)<M+\varepsilon \end{aligned}

より， $x\in B_{M+\varepsilon}(a_1)$ が示せた。故に， $A\subset B_{M+\varepsilon}(a_1)$ となるから， $A$ は有界である。

証明終

全有界の例・そうでない例

例1（ユークリッド空間）

$d$ 次元ユークリッド空間 $\R^d$ における部分集合 $[-1,1]^d$ は有界であり，全有界でもある。

$\varepsilon>0$ に対し， $[-1,1]^d\subset B_{\sqrt{d}+\varepsilon}(0)$ ですから， $[-1,1]^d$ は有界です。

一般に，ユークリッド空間 $\R^d$ における有界集合 $A$ は全有界です。証明しておきましょう。

ユークリッド空間なら有界 ⇒ 全有界の証明

$A\subset B_M(0)$ とすると， $B_M(0)\subset [-M,M]^d$ であるから， $[-M, M]^d$ が全有界であることを示せばよい。ほぼ同じことなので， $[0,1]^d$ が全有界であることを示す。

$\varepsilon >0$ とする。正の整数 $m\ge 1$ を十分大きくとることで， $1/m<\varepsilon/\sqrt{d}$ とできる。各次元の $[0,1]$ 区間を $m$ 分割してできる格子点を

D=\left\{ \left(\frac{k_1}{m}, \dots, \frac{k_d}{m}\right)\middle| 0\le k_1, \dots, k_d\le m\right\}

とすると， $[0,1]^d\subset \bigcup_{a\in D}B_\varepsilon(a)$ となっている。よって全有界である。

証明終

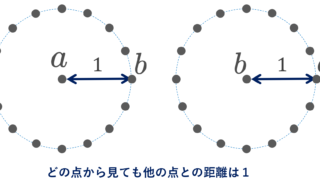
例2（離散距離）

$X$ を無限集合とし， $d(x,y)=\begin{cases} 1 & x\ne y, \\ 0 & x=y\end{cases}$ とすると， $(X,d)$ は距離空間となる(離散距離空間 (discrete metric space) という)。

この空間は有界であるが，全有界ではない。

$a\in X$ に対し， $X\subset B_2(a)$ ですから，有界です。一方で， $0<\varepsilon\le 1$ とすると， $B_\varepsilon (a)=\{a\}$ ですから，半径 $\varepsilon$ の有限個の円板で $X$ は覆えません。よって全有界でないです。

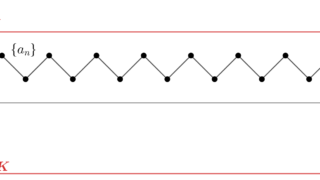
例3（無限次元空間）

二乗和が収束する実数列空間 $\ell^2=\{ \{a_n\}\subset\R\mid \sum_n |a_n|^2 <\infty\}$ について，

d(\{a_n\}, \{b_n\})=\sqrt{\sum_n |a_n-b_n|^2}

と定めることで， $(\ell^2, d)$ は距離空間と思える(より一般にヒルベルト空間と思える)。このとき，

B_1(0) =\left\{ \{a_n\}\subset\R\middle| \sum_n |a_n|^2 < 1\right\}

は有界部分集合であるが，全有界ではない。

全有界でないことは，次のように示せます。

まず， $s^{(j)}\in B_1(0)$ を前から $j$ 番目の数だけ $1/2$ で残りの数が $0$ であるような数列とします。 $i\ne j$ のとき， $d(s^{(i)}, s^{(j)})=1/\sqrt{2}$ なので， $0<\varepsilon<1/2\sqrt{2}$ とすれば，どの異なる $s^{(j)}$ も同じ円板 $B_\varepsilon (a)$ に入らないようにできます。

したがって，無限個の $s^{(1)}, s^{(2)},\dots$ を覆うためには，半径 $\varepsilon$ の円板を無限個用意する必要があり， $B_1(0)$ を半径 $\varepsilon$ の有限個の円板で覆うことができないことが分かりますね。