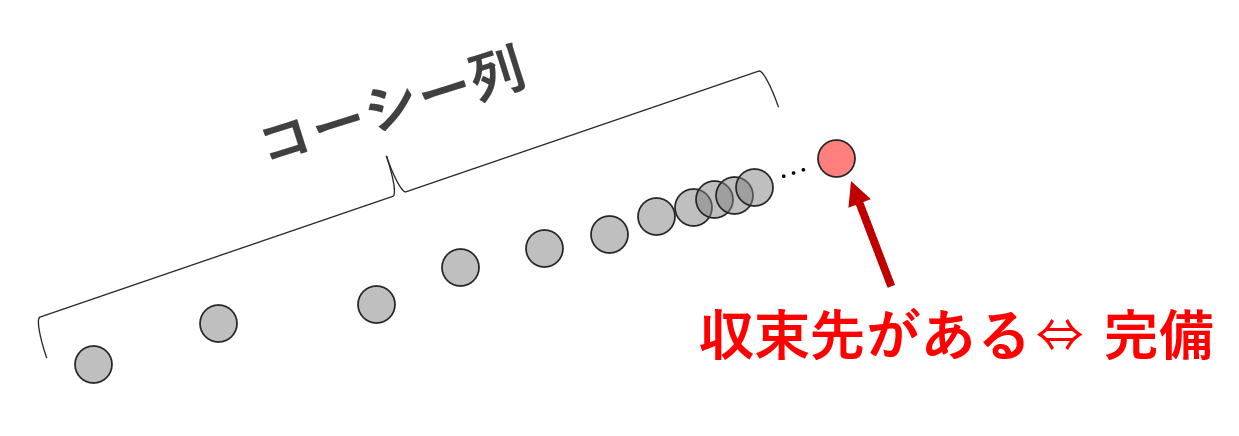
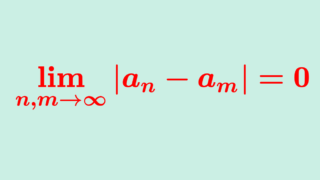数学において,完備 (complete) であるとは,コーシー列が常に(自身の中で)収束することを指します。これについて,「実数における完備性」と「距離空間における完備性」を分けて解説しましょう。
実数における完備性
完備性の定義には,コーシー列の概念が必要です。数における「コーシー列」の概念について,復習しておきましょう。
実数または複素数またはその部分集合の列 \{a_n\} がコーシー列 (Cauchy sequence) であるとは,
任意の \varepsilon >0 に対し,ある N\ge 1 が存在して,
n,m \ge N \implies |a_n -a_m|<\varepsilon
となることをいう。
要するに, n,m を大きくしていけば,差 |a_n-a_m| はどんどん小さくなるということです。
数における「コーシー列」の基本的なことについては,以下でも解説しています。
さて,これを用いて「完備性」が定義されます。定義を述べましょう。
定義(数の集合における完備性)
A\subset \mathbb{R} \;(\mathbb{C}) とする。集合 A が完備 (complete) であるとは,A 上の任意のコーシー列 \{a_n\} \subset A が A 上の点に収束することである。
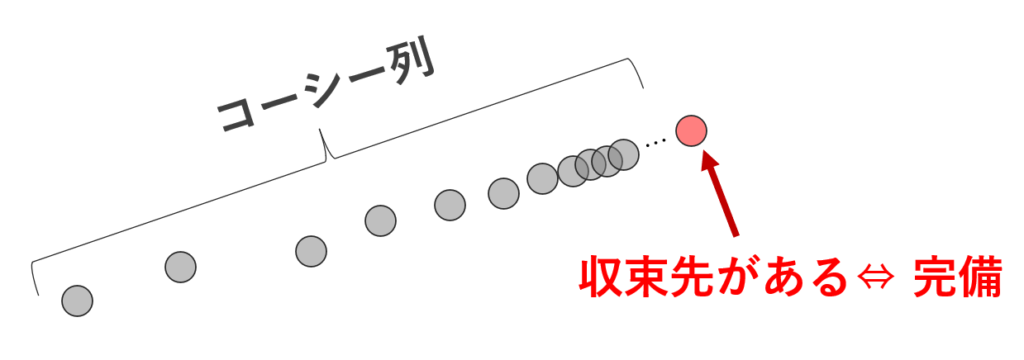
「完備」とは,「コーシー列 \iff 収束列」であることといえます。そして,次の定理が重要です。
定理(実数や複素数の集合は完備である)
\mathbb{R} や \mathbb{C} は完備である。
すなわち,コーシー列 \{a_n\} \subset \mathbb{R}\; (\mathbb{C}) は \mathbb{R} \; (\mathbb{C}) 上に収束値を持つ。
これの証明は,【微分積分学】コーシー列とは~定義と収束性の証明~で行っていますので,ここでは省略します。大事なのは,次の完備でない例を理解することです。
例1(有理数は完備でない).
\mathbb{Q} は完備でない。実際, a_n を円周率 \pi を小数表示したときの第 n 桁までの数とする。すなわち,
\begin{aligned}a_1 &= 3.1, \\ a_2&= 3.14, \\ a_3 &= 3.141, \\ a_4 &= 3.1415, \\ &\vdots \end{aligned}
と定める。このとき, \{a_n\}\subset \mathbb{Q} であり,これはコーシー列であるが,収束値について a_n \xrightarrow{n\to\infty} \pi \notin \mathbb{Q} となるので, \mathbb{Q} は完備でない。
有理数と実数の決定的な違いは,コーシー列が,ちゃんと自身の集合の中で収束するか(完備かどうか)どうかです。
有理数も実数も,どちらも「無限に敷き詰められている」状態ですが(「稠密(ちゅうみつ)」といいます→有理数・無理数の稠密性の定義とその証明),その2者には大きな違いがあるわけです。
距離空間における完備性
ここからは,より一般に,距離空間における完備性を見ていきましょう。距離空間とは,距離が考えられる空間のことで,以下で解説しています。
たとえば,実数ないしは複素数の集合は, d(x,y)=|x-y| によって距離空間と思えます。この点で,距離空間は,実数・複素数のような数の集合をさらに一般化したものです。
「距離空間の完備性」を定義する前に,距離空間における「コーシー列」を定義しましょう。数のときと矛盾の無いよう定義します。
定義(距離空間におけるコーシー列)
(X, d) を距離空間とし, \{ a_n\}\subset X とする。これがコーシー列 (Cauchy sequence) であるとは,
任意の \varepsilon >0 に対し,ある N \ge 1 が存在して,
n,m \ge N \implies d(a_n ,a_m)<\varepsilon
となることをいう。
数のときのコーシー列の定義とほぼ同じですね。 |a_n-a_m| が d(a_n,a_m) に変わっただけです。
さて,これをもとに,「距離空間の完備性」を定義しましょう。
定義(距離空間の完備性)
(X,d) は距離空間とする。 X が完備 (complete) であるとは, X における任意のコーシー列が収束列になる(収束先が X 上に存在する)ことである。
完備である距離空間を完備距離空間 (complete metric space) という。
距離空間の部分集合 A についても,同様に完備かどうかを考えることが可能です。
今回は「関数空間」を例に,完備な距離空間と,そうでない例を挙げましょう。
例2(完備な関数空間・そうでない関数空間の例).
C_0(\mathbb{R}) = \{ f\colon \mathbb{R}\to\mathbb{R}\mid f\text{ is continuous and } f(x)\xrightarrow{x\to\pm\infty} 0\}
を,無限遠で消える実数値連続関数全体の集合とし,
を, f(x) \ne 0 となる x が有界 (bounded) となる実数値連続関数全体の集合とする(専門的にはコンパクト台を持つ連続関数という)。特に C_c(\mathbb{R})\subset C_0(\mathbb{R}) である。
C_0(\mathbb{R}), C_c(\mathbb{R}) はどちらも
d(f,g) =\sup_{x\in\mathbb{R}} |f(x)-g(x)|
によって距離空間になるが, C_0(\mathbb{R}) は完備で, C_c(\mathbb{R}) は完備でない。
C_0(\mathbb{R}) が完備であることの証明は少々難しいので,ここでは省略します(バナッハ空間とは~定義と具体例5つ~の中で証明しています)。
C_c(\mathbb{R}) が完備でないことの証明は簡単なので,ここで紹介しましょう。たとえば, f(x)=e^{-x^2} とし, f_n(x) は e^{-x^2}1_{[-n,n]}(x) を「いい感じに」連続関数に補正したものとします(下図参照)( 1 は定義関数(特性関数))。
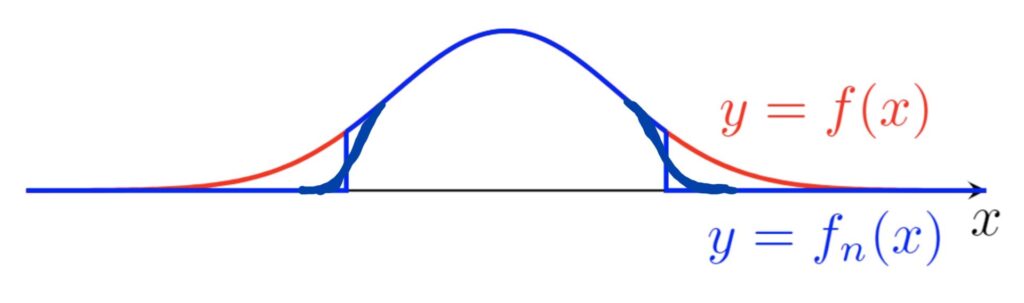
このとき, \{f_n\} \subset C_c(\mathbb{R}) であり,これはコーシー列になっています。実際, d(f_n, f_m) \le e^{-\min\{n, m\}^2} ですから,コーシー列です。さらに,
ですから, \{f_n\} は f に収束します。しかし, f\in C_0(\mathbb{R})\setminus C_c(\mathbb{R}) ですから,これは, \{f_n\} が C_c(\mathbb{R}) 上の関数に収束しないことを意味しており, C_c(\mathbb{R}) は完備ではありません。
なお, C_c(\mathbb{R}) を完備になるような最小拡張は, C_0(\mathbb{R}) であることが知られています。このように,完備な拡張を考えることを完備化 (completion) といいます。任意の距離空間は完備化可能です。