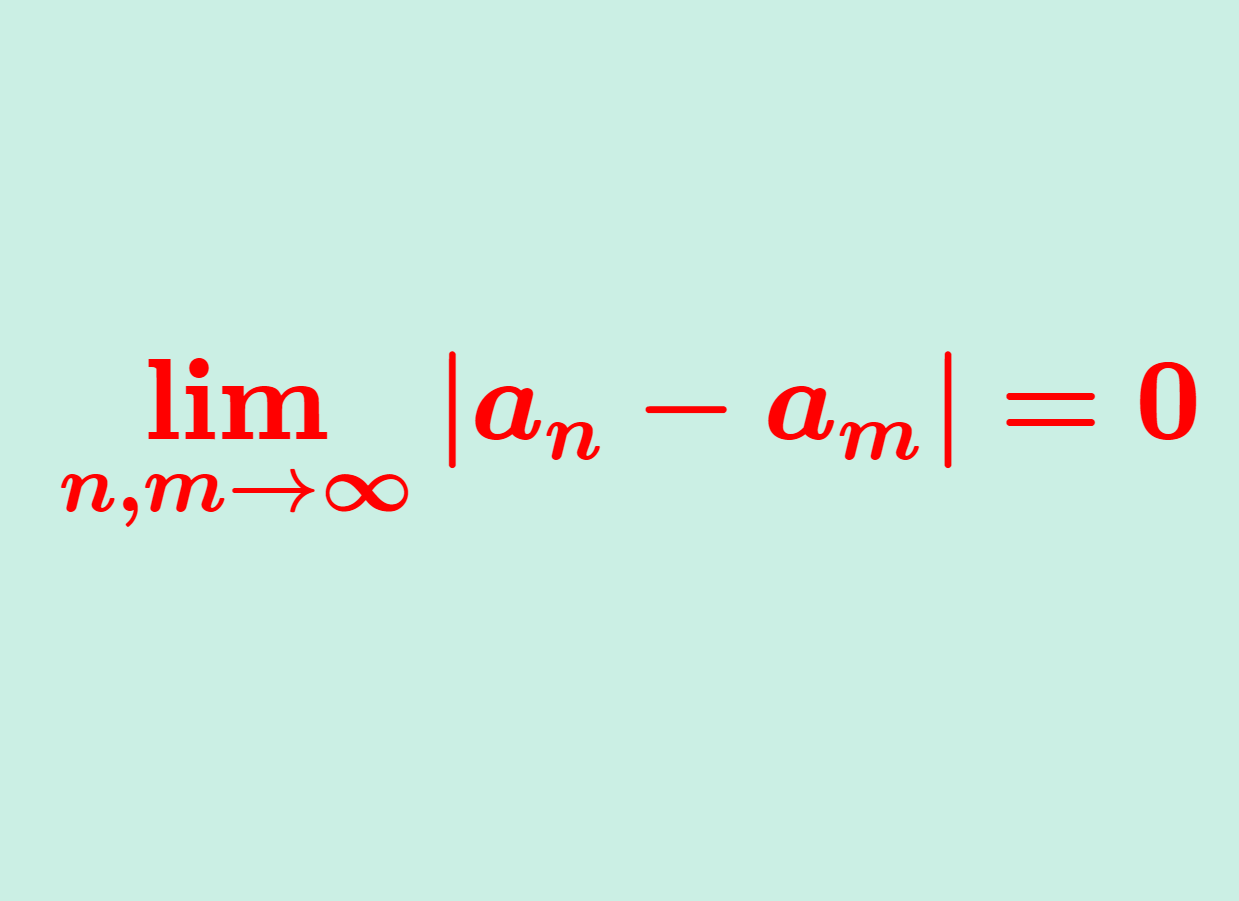【微分積分学】コーシー列とは～定義と収束性の証明～

コーシー列(基本列)は，大学1年生の微分積分学において，収束値は分からないが収束することが分かる，収束判定の道具といえます。これについて，定義と収束性の証明を行いましょう。

コーシー列の定義
コーシー列 ⇔ 収束列
コーシー列の否定
発展～より一般のコーシー列～
「収束の基本的なこと」に関する他の話題
あいまい検索

コーシー列の定義

定義（コーシー列）

実数または複素数の数列 $\{a_n\}$ がコーシー列 (Cauchy sequence) または基本列 (fundamental sequence) であるとは，

任意の $\boldsymbol{\varepsilon > 0}$ に対し，ある $\boldsymbol{N \ge 1}$ が存在して，

$\color{red} \boldsymbol{n, m \ge N \implies |a_n - a_m | < \varepsilon}$

が成立することである。これは，

\color{red} \boldsymbol{\lim_{n,m\to\infty} |a_n - a_m| = 0 }

と書いても同じことを指す。

「任意の・ある～が存在する」なんて， $\varepsilon\text{-}N$ 論法と同じ匂いがしますね(cf. イプシロンエヌ論法をわかりやすく丁寧に～数列の極限の定義～)。なお，∀(全称記号,任意の)と∃(存在記号,存在する)の使い方を知っていれば，

\forall \varepsilon>0, \exists N\ge 1,\, n,m \ge N \implies |a_n-a_m|<\varepsilon

ともかけます(本記事は分からなくても読めます)。

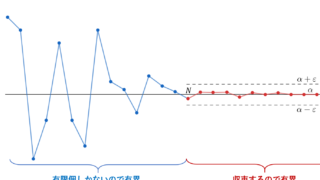
要は $n,m$ をどんどん大きくしていけば，差 $|a_n - a_m|$ はどんどん小さくなると言っています。

「差がどんどん小さくなる」とは，すなわち $\{a_n \}$ の変動はどんどん消滅していくということを意味しており，そのような数列をコーシー列というわけです。

なお， $\lim_{n,m\to\infty}$ と書いたときには， $n,m$ はそれぞれ独立・自由に $\infty$ に飛ばしていることに注意してください。

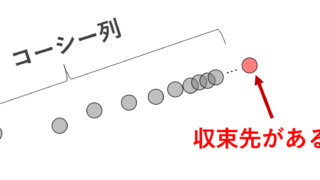
コーシー列 ⇔ 収束列

実数または複素数の数列がコーシー列であることと，収束列であることは同値であることが知られています。

コーシー列 ⇔ 収束列の定理の主張

定理（コーシー列と収束列は同値）

$\{a_n\}$ を実数列または複素数列とする。このとき，

$\{a_n\}$ が収束列 $\iff \{a_n\}$ がコーシー列

これにより， $\{a_n\}$ が収束することを判定するのには，コーシー列であるかどうかを調べればよいことが分かります。このことより，コーシー列のことをコーシーの(収束)判定条件ということもあります。

ただし，コーシー列であることが分かったところで，収束する「値」までは分からないことに注意しましょう。

なお， $\mathbb{R}$ と同様に，複素数の集合 $\mathbb{C}$ でも同様のことが成立します(証明はたとえば，実部と虚部に分ければ実数のときと同じです)。

コーシー列 ⇔ 収束列の証明

早速証明しましょう。前提知識として，以下の２つが必要です。

数列の極限の定義 (→イプシロンエヌ論法をわかりやすく丁寧に～数列の極限の定義～)
有界列は収束部分列を持つ (→ボルツァノ–ワイエルシュトラスの定理とその証明)

証明

収束列 $\implies$ コーシー列について

$\lim_{n\to\infty} a_n = \alpha$ とする。
$\varepsilon > 0$ とすると，ある $N \ge 1$ が存在して，

n \ge N \implies |a_n - \alpha | < \varepsilon

である。これから， $n, m \ge N$ のとき

\begin{aligned} |a_n - a_m | &\le |a_n - \alpha| + |\alpha - a_m| \\ &< \varepsilon + \varepsilon = 2\varepsilon \end{aligned}

となるから， $\{a_n \}$ はコーシー列である。

コーシー列 $\implies$ 収束列について

まず，コーシー列は有界であることを示そう。 $\varepsilon > 0$ とすると，コーシー列の定義と三角不等式から，ある $N \ge n$ が存在して，

n \ge N \implies |a_n| \le |a_N| + \varepsilon

となるため， $M = \max\{|a_1|,\dots, |a_{N-1}|, |a_N|+\varepsilon \}$ とおけば， $|a_n| \le M \,\, (n \ge 1)$ となる。これは有界を意味する。

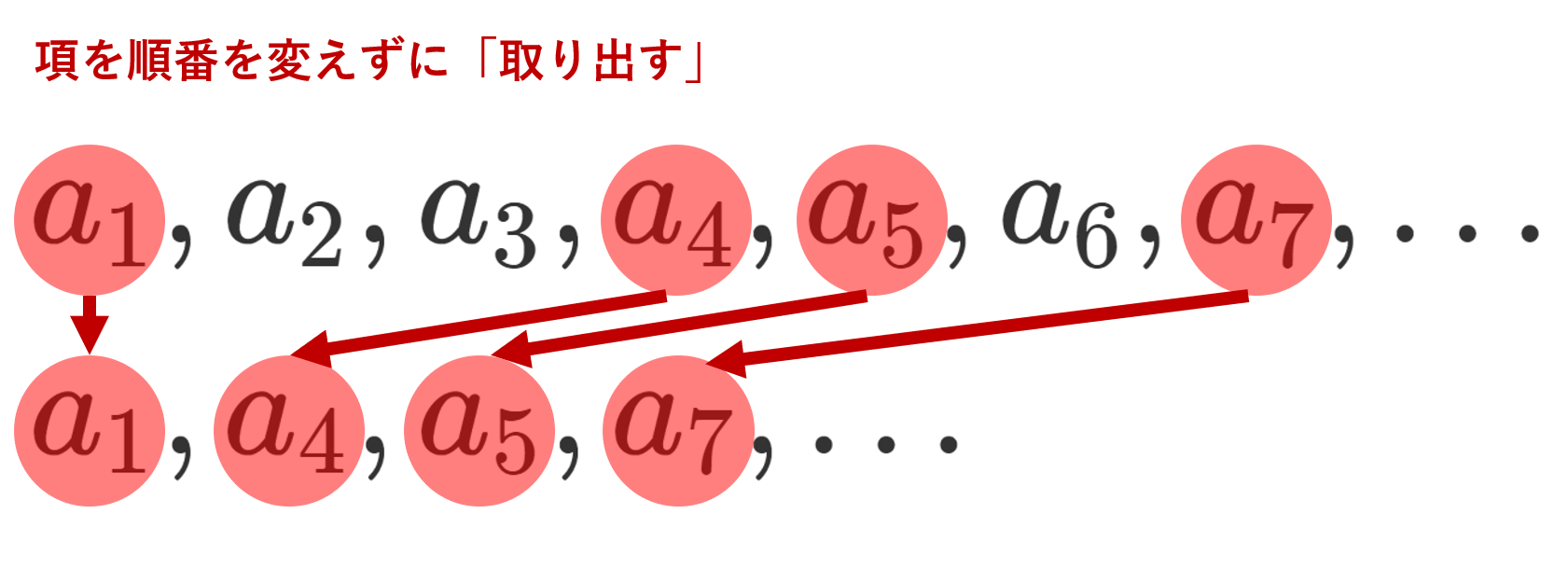
以上で有界性が示せたから，ボルツァノ－ワイエルシュトラスの定理により，収束部分列 $\{a_{n_k}\}$ が存在する。
$\lim_{k\to\infty} a_{n_k} = \alpha$ としよう。すると，ある $K \ge 1$ が存在して，

k \ge K \implies |a_{n_k} - \alpha| < \varepsilon

となる。ここで， $\widetilde{N} = \max\{ N, n_K\}$ おく。上のことと，コーシー列の定義により， $n,n_k \ge \widetilde{N}$ に対して，

\begin{aligned} |a_n - \alpha| &\le |a_n - a_{n_k}| + |a_{n_k} - \alpha| \\ &< \varepsilon+\varepsilon = 2\varepsilon \end{aligned}

である。これは， $\lim_{n\to\infty} a_n = \alpha$ を意味する。

証明終

証明の途中で，「コーシー列は有界」を示しましたが，本定理よりもちろん「収束列は有界」です。これについては，以下の記事でも解説していますから，参照してみてください。

コーシー列 ⇔ 収束列を使った証明の具体例

「証明において，コーシー列を示すことで収束列を示す」定理の具体例を挙げておきましょう。どれも「収束値はわからない」という点に注意してください。

Check～コーシー列 ⇔ 収束列を使った証明の具体例～

これらはどれも，級数に対して，コーシー列を用いています。級数に対してコーシー列を用いる時は， $\{S_n= \sum_{k=1}^n a_k \}$ がコーシー列となるので，

\begin{aligned} |S_n - S_m| &= \left|\sum_{k=m+1}^n a_k \right| \\ &= |a_{m+1} + a_{m+2} + \dots + a_{n}| \end{aligned}

について調べねばなりません。

コーシー列の否定

コーシー列でないことも述べておきましょう。否定を取るときのポイントは，「任意の～」と「ある～～が存在する」を入れ替え，不等号を逆にすることです。

命題（コーシー列の否定）

$\{a_n\}$ がコーシー列でないとは，

ある $\varepsilon > 0$ が存在して，任意の $N \ge 1$ に対し，ある $m,n \ge N$ が存在して， $|a_n - a_m | \ge \varepsilon$

が成立することである。

発展～より一般のコーシー列～

コーシー列は，より一般の空間(距離空間)で定義されます。しかし，一般には「コーシー列 $\implies$ 収束列」は成立しません。
コーシー列であることと，収束列であることが同値となる空間のことを完備 (complete) であるといいます。

たとえば，実数・複素数の空間は「完備」ですが，有理数の空間は「完備」ではありません。詳しくは，以下で解説しています。

「収束の基本的なこと」に関する他の話題

あいまい検索

級数におけるコーシーの収束判定法 (Cauchy’s root test) とは全くの別物です。これについては，以下の記事を参照してください。