大学数学,とくに解析学の最初の登竜門といえば,主に数列の極限を定義する \varepsilon\text{-}N 論法や,主に関数の極限を定義する \varepsilon\text{-}\delta 論法でしょう。今回はそのうちの \varepsilon\text{-}N 論法についてゆっくりじっくり解説していきます。腰を据えて読み進めていきましょう。
ε-N論法【収束Ver.】を理解しよう
【収束Ver.】ε-N論法による数列の極限の定義とその「お気持ち」
\varepsilon\text{-}N 論法には,【収束Ver. 】と,【±∞ Ver.】がありますが,まずは【収束Ver.】を扱うことにしましょう。
ε-N論法による定義【収束Ver.】
まず最初に定義を述べましょう。
定義(数列の極限【収束Ver.】)
\{a_n\} を実数(または複素数)の数列とし \alpha を実数(または複素数)とする。このとき,
\lim_{n\to\infty} a_n = \alpha, \quad a_n \longrightarrow \alpha \,\, (n\to\infty)
または \{a_n\} が \alpha に収束する (converge) とは,
任意の \boldsymbol{\varepsilon > 0} に対し,ある \boldsymbol{N \ge 1} が存在して,
\boldsymbol{n \ge N \implies | a_n - \alpha| < \varepsilon}
が成立することである。このとき \alpha をその数列の極限 (limit) または極限値 (limit value) という。
逆に,どの値 \alpha にも収束しないとき, \{a_n\} は発散する (diverge) という(\varepsilon\text{-}N 論法の否定の取り方は最後にやります)。
なお,イプシロンエヌ論法の定義は,∀(全称記号,任意の)と∃(存在記号,存在する)の使い方を知っているのであれば,
\color{red}\forall \varepsilon >0,\, \exists N\ge 1,\; n\ge N \implies |a_n-\alpha|<\varepsilon
となります(本記事は知らなくても読めます)。
ともかく難しいですね。その感覚は間違っていないです。今では数学が得意な人でも,これを最初に見たとき,「難しい」「意味わからない」と思ったはずです。私も全く分からず,かなり苦戦しました。なので安心してください。
まずは定義の意味を噛み砕いていきましょう。
定義の意味を考えよう
もう一度定義を記述してみましょう。
\varepsilon \text{-} N 論法
任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,
n \ge N \implies | a_n - \alpha| < \varepsilon.「言葉の語順」と「意味」を順番に考えましょう。
言葉の語順
「任意の△△に対して,ある××が存在して 〇〇〇」という形をしています。これは,
「任意の△△に対して,”〇〇〇となる××” が存在する」
と同じ意味です。日本語ではこちらの方が自然ですが,英語では “For all △△, there exists ×× such that 〇〇〇” という語順になり,こちらに合わせた方が専門家にとって何かと都合が良いため,そうなっています。
「任意の」,「存在する」の具体的な意味
「任意」とは「すべての」と言った意味です。ここでは,どんな \varepsilon > 0 を考えても,という意味になります。
「存在する」とは,「少なくとも一つある」という意味です。もちろん二つ以上あってもよいです。
今は,「 \varepsilon に対して,ある××が存在して」なので,ここでいう××は,先ほどの△△(すなわち \varepsilon の取り方に依存します。
すなわち, \varepsilon の値を変えると, N の値もそれに応じて選び直してよいということです。これは非常に大事なことです。
そして,そのように適切に△△,すなわち N を取れば, n \ge N \implies | a_n - \alpha| < \varepsilon ということが成立する,と言っています。
意味は次の「お気持ち」の部分で考えてみましょう。
これまでのことをいったんまとめて,定義をより平易に言い換えてみましょう。
定義の平易な言い換え
どんな \varepsilon > 0 を取ってきても,それに応じて適切に N \ge 0 を1つ選んであげることで,
n \ge N \implies | a_n - \alpha| < \varepsilon
ということが成立する。
さて,定義の「言葉の意味」はある程度理解できたのではないかと思います。続いて,「お気持ち」のところを確認していきましょう。
ε-N論法の「お気持ち」
さて,「お気持ち」すなわち「感覚的な理解」について考えてみましょう。ここでは,実数の数列を扱います。
高校のときの極限の定義はどんなものだったでしょうか。
n を大きくすると, a_n が \alpha に限りなく近づくこと。
この,「限りなく近づく」の部分を厳密にしたものが \varepsilon\text{-} N 論法になるはずですね。果たして,実際にそうなっているのでしょうか。
もう一度定義を再掲します。
\varepsilon \text{-} N 論法
任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,
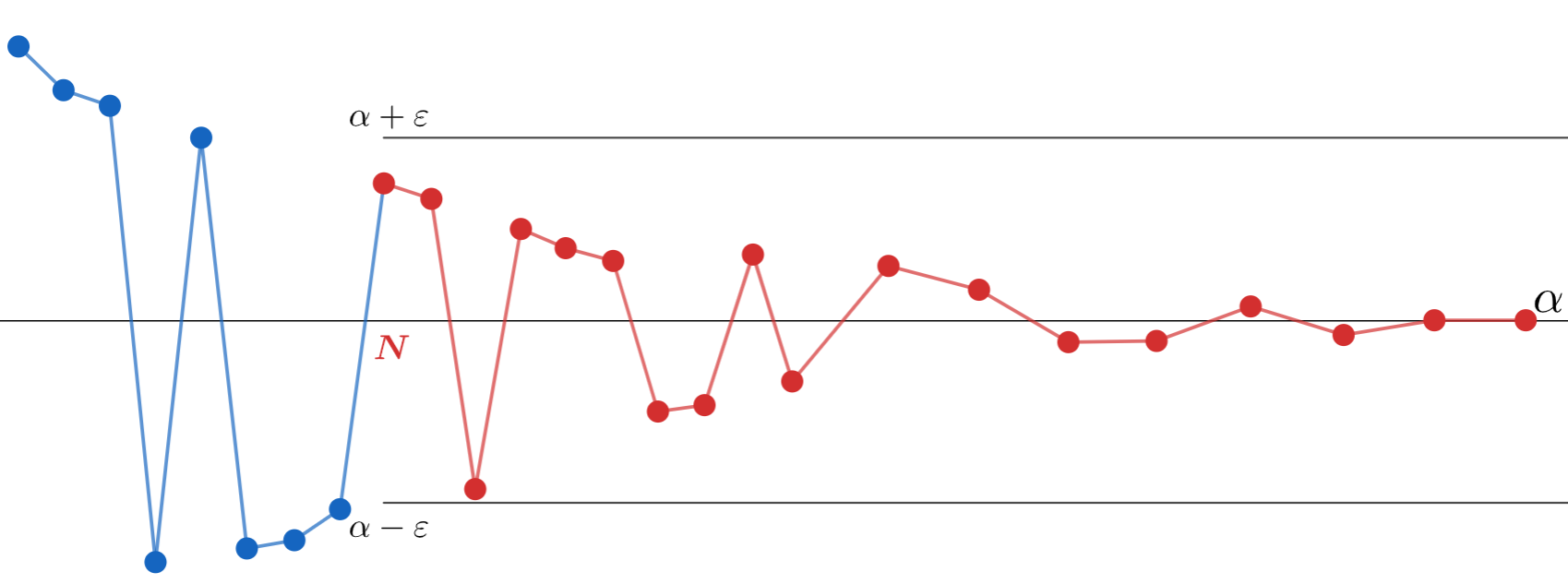
n \ge N \implies | a_n - \alpha| < \varepsilon.図で考えてみましょう。今, \varepsilon>0 を一つとってきたとします。
すると, n \ge N \implies | a_n - \alpha| < \varepsilon をみたす N が取れる,
N 以上の全ての n で | a_n - \alpha| < \varepsilon が成立するわけですから,図にすると以下のような感じになります。
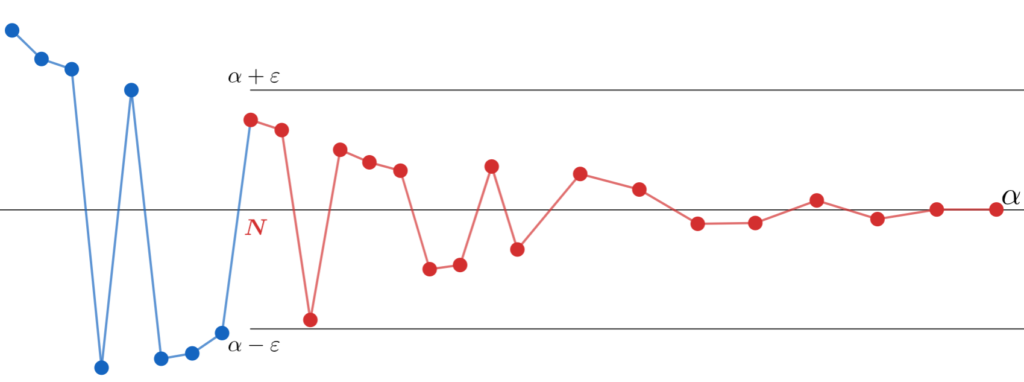
さて, \varepsilon > 0 は任意のとれる,すなわちどんな値でも良いのでした。もっと小さな \varepsilon を取ってみましょうか。 N は \varepsilon に依存するため,それに応じて, N も取り直さねばなりません。
このとき, | a_n - \alpha| < \varepsilon の制約が強くなるわけですから, N は必然的に大きくなります。
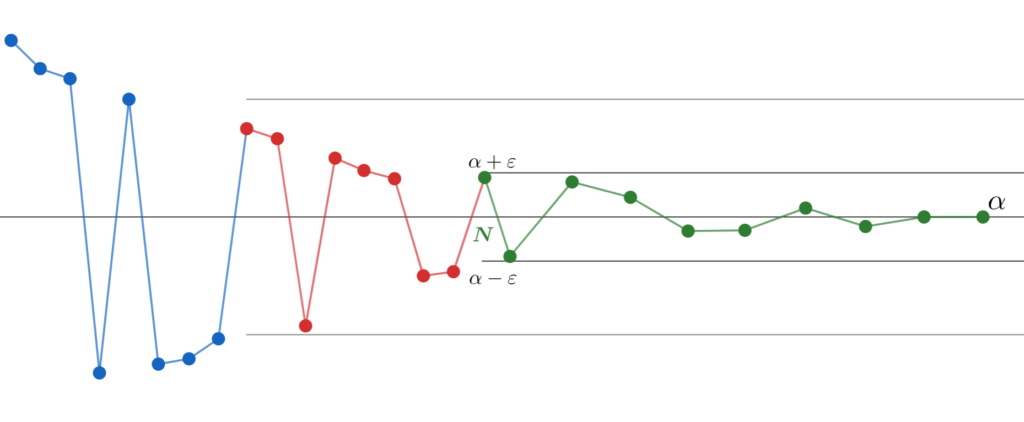
さらにもっと \varepsilon > 0 を小さく取り直してみましょう。再び N を大きく取り直さねばなりません。
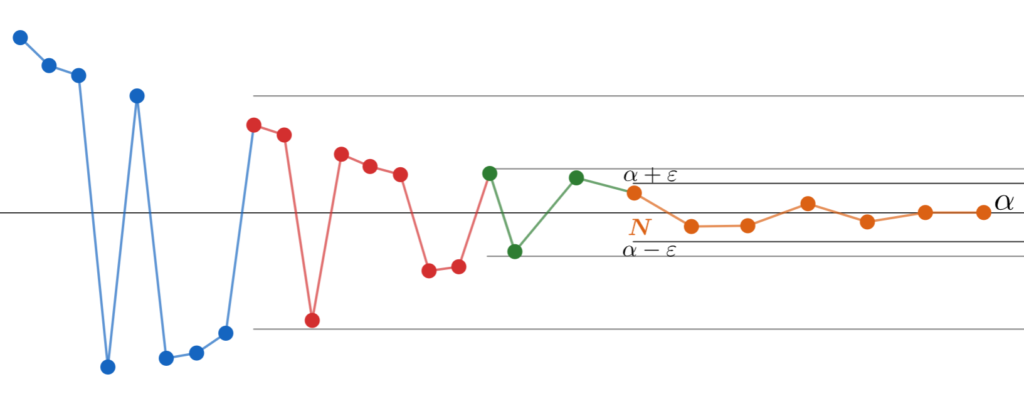
さて,これらの図を見ると,
\varepsilon > 0 が小さくなる \iff N が大きくなる
という構図になっているのが分かるのではないでしょうか。左右を入れ替えて書くと,
N が大きくなる \iff \varepsilon > 0 が小さくなる
となっていますね。さて,ここで, |a_n - \alpha | < \varepsilon となる \varepsilon > 0 が「小さくなる」とは,それすなわち「 a_n が \alpha に近づく」ことを意味しているため,
N が大きくなる \iff a_n が \alpha に近づく
ということになりますね。
これは,すなわち N を大きくすれば \{a_n\}\,\, (n\ge N) はどんどん \alpha に近づくということが,なんとなく分かるのではないでしょうか。
これが, \varepsilon \text{-} N 論法の「お気持ち」です。
\varepsilon\text{-}N 論法は,高校のときの極限の定義「 n が大きくなると \alpha に近づく」ことを言い表したものである!
【収束Ver.】具体例とともに理解を深めよう
少々難しかったかもしれません。次は具体例を通して,より理解を深めていきましょう。
考える具体例はこれだ!
例題
\color{red} \displaystyle \lim_{n\to\infty} \frac{1}{n} = 0 であることを証明せよ。
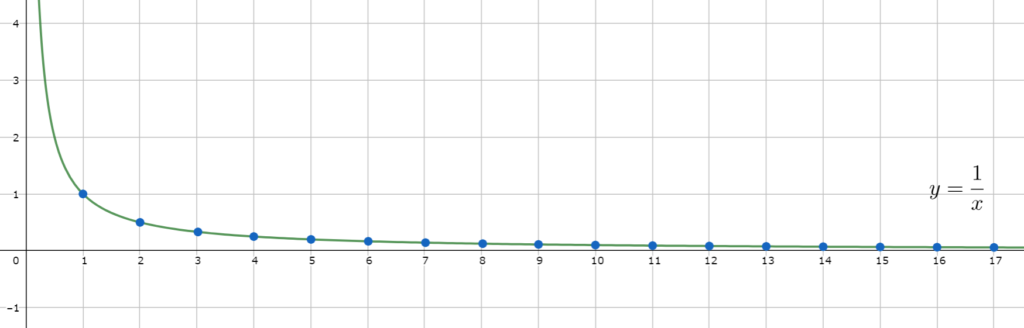
高校では,「 n が大きくなれば, 1/n はどんどん小さくなって 0 に限りなく近づくよね」と言われたと思います。その感覚はもちろん正しいですが, \varepsilon \text{-} N 論法を用いて,それが正しいのか確認していきましょう。
まず,適当な ε を取って考えよう
厳密な証明を考える前に,適当に \varepsilon > 0 を指定して,本当にそうなっているのか考えてみましょう。
まず,示すべきことを \varepsilon \text{-} N 論法で書くと以下のようになります。。
示すべきこと
任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,
n \ge N \implies \left| \frac{1}{n} \right| < \varepsilon .\varepsilon > 0 は小さくとってよかったため,はじめに \color{red} \varepsilon = 0.01 としてみましょう。
示すべきことは, n \ge N \implies | 1/n| < 0.01 となる N が存在することです。これは, \color{red} N = 101 とすると,
n \ge 101 \implies \left| \frac{1}{n} \right| < 0.01
のため, N は存在することが分かります。もちろん, N をもっと大きくとっても構いません。たとえば, N = 200 でも良いです。
では,今度は \color{red} \varepsilon = 0.0001 としましょう。 1/10000 = 0.0001 ですから,このときは,\color{red} N = 10001 とすればよいです。
さらに, \color{red} \varepsilon = 0.000001 とすると, 1/1000000 = 0.000001 なので,たとえば \color{red} N = 1000001 とすれば良いです。
これらをまとめて考えると「お気持ち」部分で解説したとおり,
\varepsilon > 0 が小さくなる \iff N が大きくなる
が成立することが分かりますね。
厳密に証明しよう
さて, \lim_{n\to\infty} 1/n = 0 であることを厳密に証明してみましょう。
\lim_{n\to\infty} 1/n =0 の証明
\varepsilon > 0 を任意に取る。このとき, 整数 N を
N = [1/\varepsilon] + 2
(ただし [\cdot ] は床関数(ガウス記号)) とすると, 1/N < \varepsilon であるから,
が成立する。これは \lim_{n\to\infty} 1/n =0 であることを意味する。
証明終
どんな \varepsilon > 0 であっても, n \ge N \implies | a_n - 0| < \varepsilon をみたす N が存在したので,定義に当てはまっており, \lim_{n\to\infty} 1/n = 0 が言えたということになります。
「存在すること」はどうやって示したかというと,具体的に N = [1/\varepsilon] + 2 と取りました。このように実際に, N の存在を証明する際は,具体的に取って見せるのが一般的です。
このとき, N は \varepsilon > 0 に依存している,すなわち \varepsilon の値を変えると N が変わっても良かったことに注意してください。
実際,今回も N = [1/\varepsilon] + 2 としたわけで,これは \varepsilon の値に依存しています。
【収束Ver.】のまとめ
さて,【収束Ver.】のまとめです。
- \lim_{n\to\infty} a_n = \alpha であるとは,どんな \varepsilon > 0 を取っても,それに応じて適切な N \ge 1 が取れて, n \ge N \implies | a_n - \alpha| < \varepsilon が成立することである。
- 上の定義は,
N が大きくなる \iff a_n が \alpha に近づく
ということを意味しており,「 n を大きくすると a_n は \alpha に限りなく近づく」といえる。 - N は \varepsilon の取り方に依存して構わない。
- N の存在を示すときは,実際に N を式で書けばよい。
これで,【収束Ver.】の基本的な説明はおしまいです。ただし後に補足がありますから,そちらも確認してください。
ε-N論法【±∞ Ver.】を理解しよう
【±∞ Ver.】ε-N論法による数列の極限の定義とその「お気持ち」
続いて,発散する場合で特に【±∞Ver.】となる場合の定義と「お気持ち」を考えます。ここまでをなんとなく理解していれば,ほぼ同様のロジックであることが分かるでしょう。
ε-N論法による定義【±∞ Ver.】
定義(数列の極限【±∞ Ver.】)
\{a_n\} を実数の数列とする。このとき,
\lim_{n\to\infty} a_n = \infty, \quad a_n \longrightarrow \infty, \,\, (n\to\infty)または \{a_n\} が \infty に発散する (diverge) とは,
任意の \boldsymbol{ K > 0 } に対し,ある \boldsymbol{N \ge 1} が存在して,
\color{red}\boldsymbol{ n \ge N \implies a_n > K}
が成立することを言う。逆に,
または \{a_n\} が -\infty に発散する (diverge) とは,
任意の \boldsymbol{ K > 0 } に対し,ある \boldsymbol{ N \ge 1} が存在して,
\color{red}\boldsymbol{ n \ge N \implies a_n < - K}
が成立することを言う。
最初に注意ですが,数列の極限は
- 収束する
- \pm \infty に発散する
- 「振動」の意味で発散する
の3種類があります。今から扱うのは,上から2番目のケースです。最後のケースは,素直に \varepsilon\text{-}N 論法を用いて書くことができません。発散するケースを全て扱えているわけではなく,あくまで \pm \infty に飛ぶもののみ扱っていることに注意してください。
今回は \varepsilon ではなく, K という文字を使いました。 \varepsilon でも良いのですが, \varepsilon は微小量を表すことが多いので,あえて別の文字にしました。大きい量を表すときは,慣習で K, L ,M, N,R あたりが使われることが多いです。
今回は +\infty に発散する方のみを考えましょう。 -\infty に発散する場合も同じです。
定義の意味を考えよう
さて,【収束Ver.】と同様に,定義の意味を考えていきましょう。
定義の式を再掲します。
任意の { K > 0 } に対し,ある N \ge 1 が存在して,
{ n \ge N \implies a_n > K}.「任意の△△に対して」や「ある××が存在して」というのは先ほどと同じですね。
よって,これを少しだけ平易な言葉で言い換えると,以下のようになります。
どんな K> 0 を取ってきても,それに応じて適切に N \ge 0 を選んであげることで,
n \ge N \implies a_n >K
ということが成立する。
ここで, N は K に依存していることに注意しましょう。
ε-N論法【発散Ver.】の「お気持ち」
さて,「お気持ち」を考えましょう。高校のときの, \lim_{n\to\infty} a_n = \infty の感覚はどんなものだったでしょうか。
n を大きくすると, a_n がどんどん大きくなること
さて,本当にそうなっているのでしょうか。
もう一度定義を再掲します。
任意の { K > 0 } に対し,ある N \ge 1 が存在して,
{ n \ge N \implies a_n > K}.再び,図で考えてみましょう。今, K>0 を一つとってきたとします。
すると, N が取れて, N より大きい全ての n で a_n > K が成立するわけですから,以下のようになりますね。
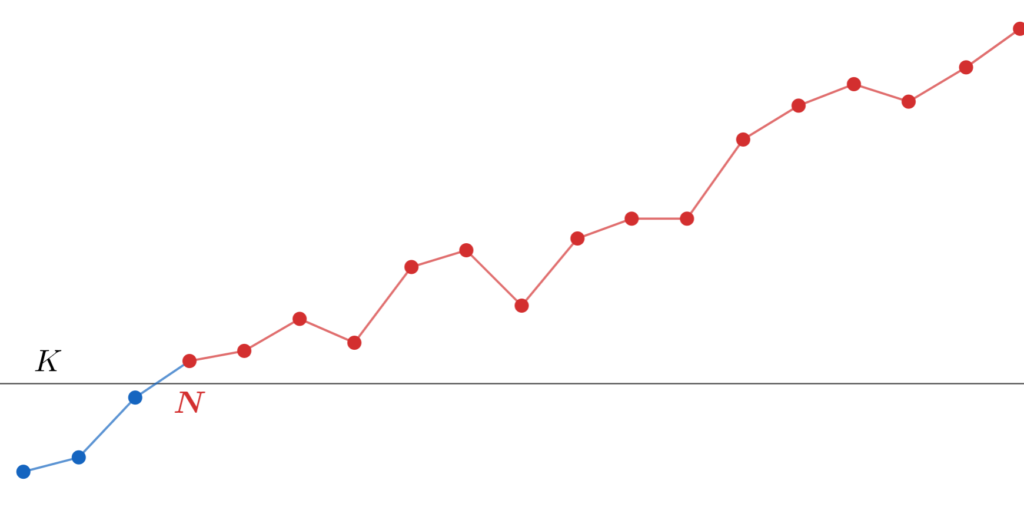
さて, K > 0 はどんな値でも良かったので。もっと大きな K をとってみましょうか。
このとき, a_n > K \,\, (n\ge N) の制約が強くなるわけですから, N は必然的に大きくなります。
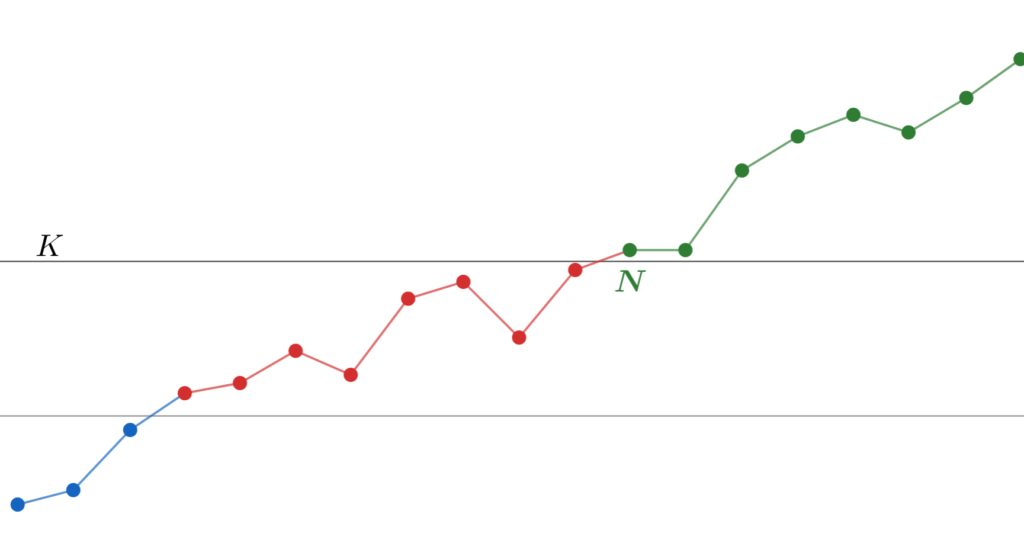
さらにもっと K > 0 を大きく取り直すと,再び N を大きく取り直さねばなりません。
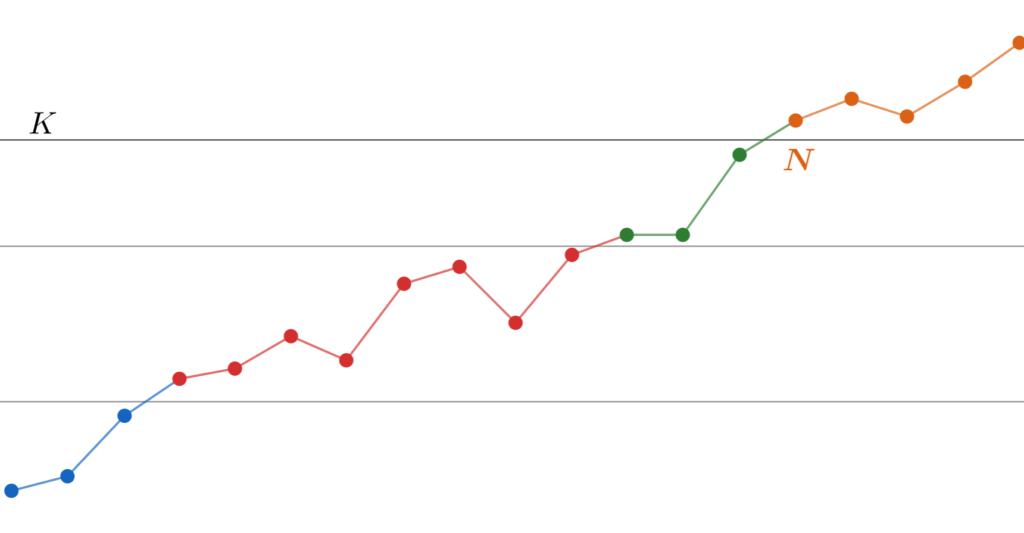
さて,これらの図を見ると,【収束Ver.】と類似していることが分かるでしょう。今回の場合は,
K > 0 が大きくなる \iff N が大きくなる
となります。単に左右を入れ替えて書き直すと,
N が大きくなる \iff K > 0 が小さくなる
となっていることが分かりますね。。ここで, a_n > K となる K > 0 が「大きくなる」とは,それすなわち「 a_n が大きくなる」ことを意味しているため,
N が大きくなる \iff a_n が 大きくなる
と言えることになります。
これは,すなわち N を大きくすれば \{a_n\}\,\, (n\ge N) はどんどん大きくなっていくということになり,高校数学のときの「∞への発散」の感覚と矛盾していないことが分かります。
これが, \varepsilon \text{-} N 論法の「お気持ち」です。
発散Ver. の \varepsilon\text{-}N 論法は,高校のときの極限の定義「 n が大きくなるとどんどん大きくなる」ことを言い表したものである!
【±∞ Ver.】具体例とともに理解を深めよう
さて,こちらも具体例を通して,より理解を深めていきましょう。
考える具体例はこれだ!
例題
\color{red} \displaystyle \lim_{n\to\infty} \sqrt{n} = \infty であることを証明せよ。
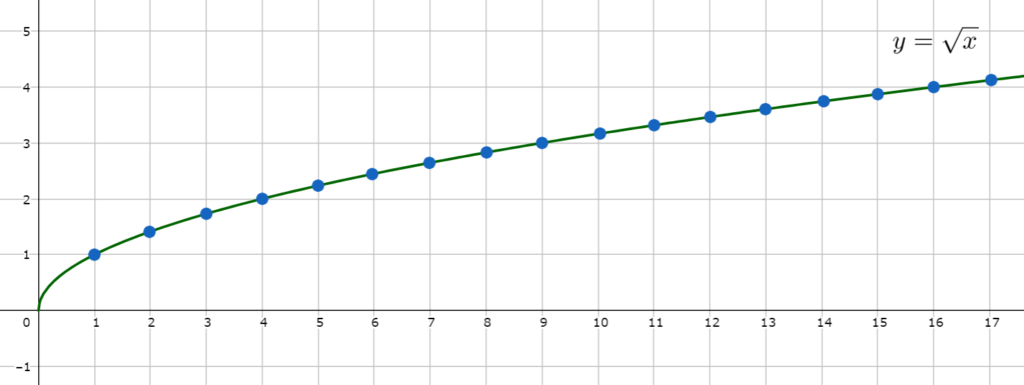
高校では,「 n が大きくなれば, \sqrt{n} は果てしなく大きくなって, \infty に飛ぶよね」と言われたかもしれません。このことを, \varepsilon \text{-} N 論法を用いて,正しいのか確認していきましょう。
まず,適当な K を取って考えよう
厳密な証明を考える前に,適当に K > 0 を指定して,本当にそうなっているのか考えてみましょう。
示すべきことを【±∞ Ver.】の \varepsilon \text{-} N 論法を用いて述べると以下のようになります。。
示すべきこと
任意の K > 0 に対し,ある N \ge 1 が存在して,
n \ge N \implies \sqrt{n} > K.さて, K > 0 をどんどん大きくしていくことにしましょう。まず \color{red} K = 10 としましょう。このとき, \color{red} N = 101 とすれば,
n \ge 100 \implies \sqrt{n} > 10
が成立します。もちろん N = 200 でも N =300 でもよいです。
次に, \color{red} K = 100 とすると, \sqrt{10000}=100 より,今度は \color{red} N = 10001 とすればよいです。さらに \color{red} k = 1000 とすると, \sqrt{1000000} = 1000 よりたとえば \color{red} N = 1000001 と取れば,条件を満たします。
以上を踏まえると,「お気持ち」部分で説明した,
K > 0 が小さくなる \iff N が大きくなる
が確かに成立することが,具体例を通して確認できましたね。
厳密に証明しよう
さて, \lim_{n\to\infty} \sqrt{n} = \infty であることを厳密に証明することにしましょう。
\lim_{n\to\infty} \sqrt{n} = \infty の証明
\varepsilon > 0 を任意に取る。このとき, 整数 N を
N = K^2 + 1
(ただし [\cdot ] は床関数(ガウス記号)) とすると,
が成立する。これは \lim_{n\to\infty} \sqrt{n} = \infty であることを意味する。
証明終
どんな K > 0 であっても, n \ge N \implies a_n > K をみたす N が存在したので,定義に当てはまっており, \lim_{n\to\infty} \sqrt{n}= \infty が分かりました。
「存在すること」はどうやって示したかというと,具体的に N = K^2 + 1 と,存在証明のために,具体的に取りました。 【収束Ver.】のときと同じですね。
このとき, N は K > 0 に依存していることに注意してください。
実際,今回も N = [1/\varepsilon] + 2 としたわけで,これは \varepsilon の値に依存しています。
【±∞ Ver.】のまとめ
さて,【±∞ Ver.】のまとめです。
- \lim_{n\to\infty} a_n = \infty であるとは,どんな K > 0 を取っても,それに応じて適切な N \ge 1 が取れて, n \ge N \implies a_n > K が成立することである。
- 上の定義は,
N が大きくなる \iff a_n が 大きくなる
ということを意味しており,「 n を大きくすると a_n は限りなく大きくなる」といえる。 - N は K の取り方に依存して構わない。
- N の存在を示すときは,実際に N を式で書けばよい。
これで,【±∞ Ver.】の説明も終わりです。
ε-N論法の定義における重要な補足
さて,ここで重要な補足をしておきましょう。 \varepsilon\text{-}N 論法の定義は,時と場合によって書き方が変わることがあります。まずは【収束Ver.】について確認しましょう。
補足( \varepsilon\text{-}N 論法の同値な定義【収束Ver.】)
以下は全て同値である。
- 任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies | a_n - \alpha| < \varepsilon.
- 任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies | a_n - \alpha| < \textcolor{red}{\boldsymbol{k}} \varepsilon. ただし, k > 0 は N,\varepsilon に依存しない定数。
- 任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies | a_n - \alpha| \textcolor{red}{\boldsymbol{\le}} \varepsilon.
- 任意の 0<\varepsilon \textcolor{red}{\boldsymbol{< l}} に対し,ある N \ge 1 が存在して, n \ge N \implies | a_n - \alpha| < \varepsilon. ただし, l > 0 は N,\varepsilon に依存しない定数。
- 任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,任意の n \ge N に対し,| a_n - \alpha| < \varepsilon が成立する。
- 任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,| a_n - \alpha| < \varepsilon \,\, (n \ge N) が成立する。
それぞれが同値であることを説明しておきましょう。
説明
1. \iff 2. について:
「任意の \varepsilon > 0 に対して」と「任意の k\varepsilon > 0 に対して」は「同じこと」(後ろの議論に影響がない)であるのでOK。
1. \iff 3. について:
| a_n - \alpha| < \varepsilon \implies | a_n - \alpha| \le \varepsilon より, \implies は明らか。
3. を \varepsilon の代わりに \varepsilon / 2 として考えると, | a_n - \alpha| \le \varepsilon/2 < \varepsilon となるため,1. は成立。
1. \iff 4. について:
\varepsilon \ge l のときは, n \ge N \implies |a_n-\alpha| < l となる N\ge 1 を取れば, n \ge N \implies |a_n-\alpha| < \varepsilon をみたすのでよい。
1. \iff 5. \iff 6. について:
「 n \ge N \implies | a_n - \alpha| < \varepsilon 」と
「任意の n \ge N に対して,| a_n - \alpha| < \varepsilon」と
「| a_n - \alpha| < \varepsilon \,\, (n\ge N ) 」
は同義なので同値である。
説明終
【±∞ Ver.】についても述べておきます。と言っても,【+∞ Ver.】 のみ扱うことにしましょう。
補足( \varepsilon\text{-}N 論法の同値な定義【+∞ Ver.】)
以下は全て同値である。
- 任意の K > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies a_n > K.
- 任意の K > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies a_n > \textcolor{red}{\boldsymbol{k}} K. ただし, k > 0 は N ,\varepsilon に依存しない定数。
- 任意の K > 0 に対し,ある N \ge 1 が存在して, n \ge N \implies a_n \textcolor{red}{\boldsymbol{\ge}} K.
- 任意の K > \textcolor{red}{\boldsymbol{R} } に対し,ある N \ge 1 が存在して, n \ge N \implies a_n > K. ただし, R> 0 は N ,\varepsilon に依存しない定数。
- 任意の K > 0 に対し,ある N \ge 1 が存在して,任意の n \ge N に対し,a_n > K が成立する。
- 任意の K > 0 に対し,ある N \ge 1 が存在して,a_n > K \,\, (n \ge N) が成立する。
実際の場面では,さまざまな書き方がされるため,どの書き方がされても対応できるようにしておきましょう。
ε-N論法の否定
さて, \varepsilon\text{-}N 論法は,否定を取って使いたい場面も多いと思うので紹介します。
否定を取るときのポイントは,文中における全ての「任意の」と「ある~が存在する」を入れ替えることです。上の 5. の否定を取ると考えるのが分かりやすいでしょう。【収束Ver.】【±∞ Ver.】に分けて考えましょう。
ε-N論法の否定【収束Ver.】
主張
命題( \varepsilon\text{-}N 論法の否定【収束Ver.】)
数列 \{a_n\} が \alpha に収束しないとは,
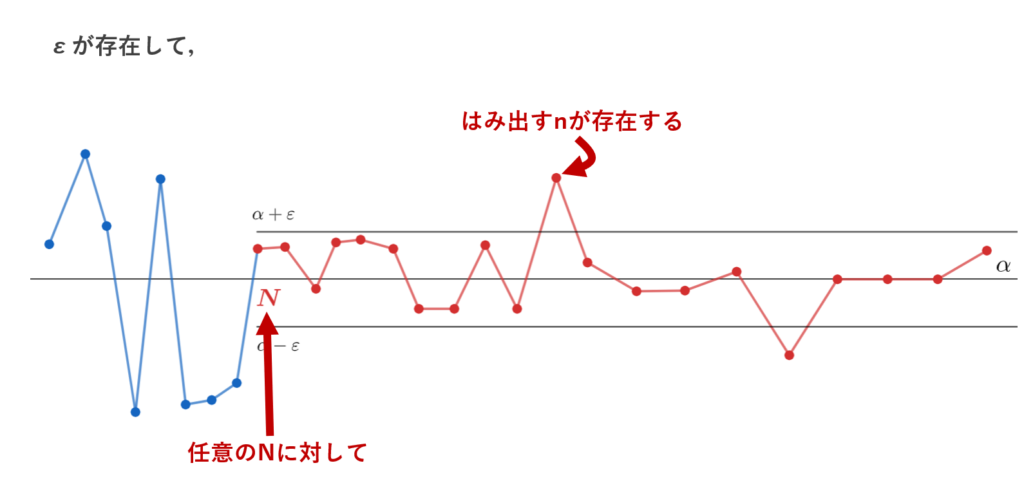
ある \varepsilon > 0 が存在して,任意の N \ge 1 に対し,ある n \ge N が存在して, |a_n - \alpha| \ge \varepsilon が成立することである。
最初に注意ですが,これは \{a_n\} は \alpha に収束しないと言っているだけで,他の値に収束している可能性もありますし,発散している可能性もあります。
元の定義と比較してみましょう。1が \varepsilon\text{-}N 論法の定義で,2がその否定です。
- (元の定義)任意の \varepsilon > 0 に対し,ある N \ge 1 が存在して,任意の n \ge N に対し,| a_n - \alpha| < \varepsilon が成立する。
- (否定の定義)ある \varepsilon > 0 が存在して,任意の N \ge 1 に対し,ある n \ge N が存在して, |a_n - \alpha| \ge \varepsilon が成立することである。
「任意の」と「ある~が存在する」が入れ替わっていますね。最後の不等号も入れ替わっています。
否定の言葉の意味
定義の意味を少しだけ考えてみましょう。「~に対して」は「依存する」ということでしたから,各変数の依存関係を考えつつ主張を分解すると以下のようになります。
- \varepsilon > 0 が一つ存在して,以下が成立
- 任意の N \ge 1 に対して,
- ある N, \varepsilon に依存する n \ge N が存在して,
- |a_n-\alpha| \ge \varepsilon となる
まず,最初の \varepsilon については,他の変数に依存することはありません。
その次の N について「任意の」とは「全ての値を取る」ので他の変数に依存することはありません。
その次の, n の存在性は N , \varepsilon に依存します。
否定の「お気持ち」【収束Ver.】
「お気持ち」を図で描くと以下のようになります。
ε-N論法の否定【±∞ Ver.】
さて,こちらについては主張と「お気持ち」の図だけ述べることにしましょう。
主張
命題( \varepsilon\text{-}N 論法の否定【±∞Ver.】)
数列 \{a_n\} が \infty に発散しないとは,
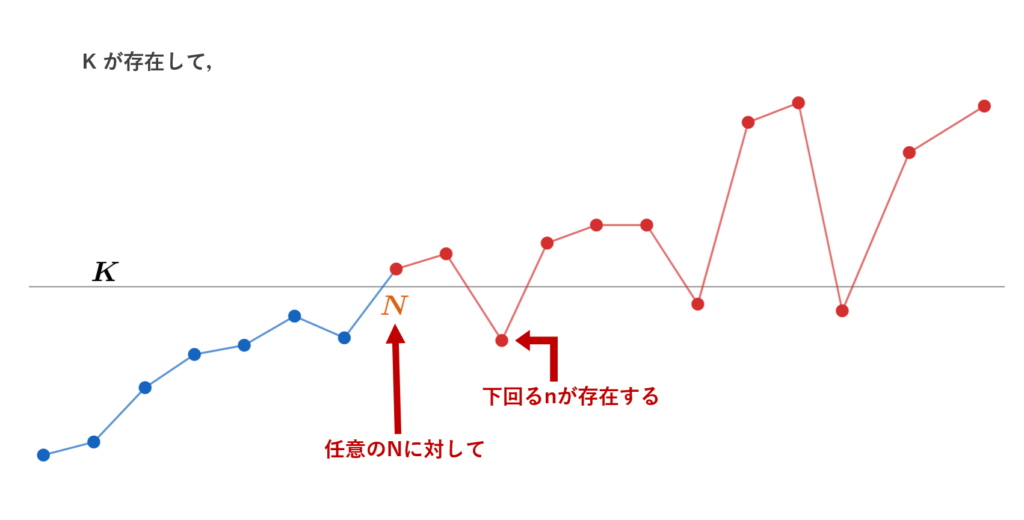
ある K > 0 が存在して,任意の N \ge 1 に対し,ある n \ge N が存在して, a_n \le K が成立することである。
また,数列 \{a_n\} が -\infty に発散しないとは,
ある K > 0 が存在して,任意の N \ge 1 に対し,ある n \ge N が存在して, a_n \ge -K が成立することである。
否定の「お気持ち」【+∞ Ver.】
「お気持ち」を図で表すと以下のようになります。
数列の極限の性質
さて,定義の以上で終わりです。最後に,極限の基本的な性質を列挙してみましょう。
定理(数列の極限の性質)
以下, \{a_n\}, \{b_n\}, \{c_n\} を数列とし, \alpha, \beta \in \mathbb{R} (実数) とする。このとき,
- \displaystyle\alpha= \lim_{n\to\infty} a_n, \, \beta=\lim_{n\to\infty} a_n ならば, \displaystyle \alpha = \beta である。すなわち,極限は存在すれば一意に定まる。
- \{a_n\} が収束すれば有界,すなわち |a_n| < K \,\, (n\ge 1) となる K > 0 が存在する。
- a_n \ge 0 \,\,(n\ge 1) かつ \displaystyle \alpha = \lim_{n\to\infty} a_n ならば, \alpha \ge 0 .
- \displaystyle \alpha= \lim_{n\to\infty} a_n, \, \beta=\lim_{n\to\infty} b_n ならば,
- \displaystyle \alpha + \beta = \lim_{n\to\infty} (a_n+b_n) .
- \displaystyle \alpha\beta = \lim_{n\to\infty} a_nb_n .
- \displaystyle \alpha= \lim_{n\to\infty} a_n \ne 0 ならば,\displaystyle \frac{1}{\alpha} = \lim_{n\to\infty} \frac{1}{a_n} .
- a_n > 0 \,\,(n\ge 1) かつ \displaystyle \lim_{n\to\infty} a_n = 0 ならば, \displaystyle \lim_{n\to\infty}\frac{1}{ a_n} = \infty .
- a_n \le c_n \le b_n \,\,(n\ge 1) かつ \displaystyle \alpha = \lim_{n\to\infty} a_n =\lim_{n\to\infty} b_n とすると, \displaystyle \lim_{n\to\infty} c_n = \alpha. (はさみうちの原理)
- b_n \ge a_n \,\,(n\ge 1) かつ \displaystyle \alpha = \lim_{n\to\infty} a_n = \infty とすると,\displaystyle \lim_{n\to\infty} b_n = \infty. (追い出しの原理)
- \displaystyle \alpha = \lim_{n\to\infty} a_n ならば,\displaystyle \alpha = \lim_{n\to\infty} \frac{a_1 + a_2 + \cdots +a_n}{n} . (平均値の収束)
演習問題としても最適ですから,もし自分で考えられるなら,考えてみましょう。
実際のところは,ある程度慣れていないと厳しいかもしれません。そういう時は,以下を参照するとよいでしょう。読んで理解するだけでも身につきます。
- 極限の性質6つの証明(一意性,和,積,商,大小関係)
- 収束する数列は有界であることの証明
- はさみうちの原理とその厳密な証明~数列版・関数版~
- 追い出しの原理とその厳密な証明~数列版・関数版~
- 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明
また,他にも以下の性質は基本的です。
関数の極限を定義する ε-δ 論法
\varepsilon\text{-}N 論法を習った次のステップは,関数の極限を定義する \varepsilon\text{-}\delta 論法でしょう。理屈は今回とほぼ同じですが,以下に別途解説していますので,確認してみてください。
おわりに
大幅に長い記事になってしまいました。ここまでなんとなくでも理解できれば,あとは慣れです。
さまざまな証明をみたり,自分で \varepsilon\text{-}N 論法を展開したりしているうちに,だんだんわかってくるものです。
大切なのは,いま100%理解することではありません。有名な数学者だって,スグに理解できた人は少なかったと思います。本当に大切なのは,「ごまかさず,きちんと今後も \varepsilon\text{-}N 論法に向き合うこと」です。そうすれば,年単位で時間がかかるかもしれませんが,いずれ分かるようにるはずです。
分からなければ,何度もこのサイトを読み返してみてもよいでしょう。またいつでも,このページに戻ってきてください。
大学数学における解析学の道は,ここからスタートです。