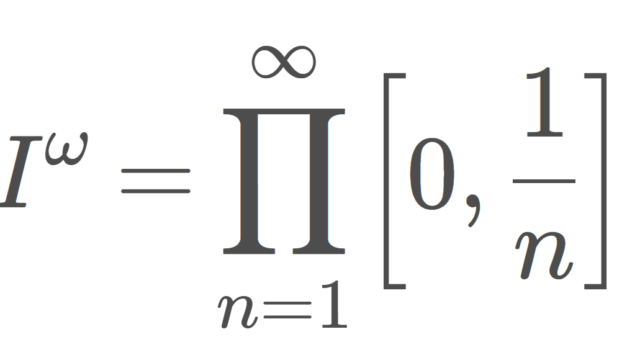 集合と位相
集合と位相 ヒルベルト立方体(Hilbert cube)の定義と位相的性質
ヒルベルト立方体とは,閉区間の可算個の直積で定義される位相空間で,距離化可能な空間,2乗可積分な数列のなすヒルベルト空間の部分集合です。ヒルベルト立方体について,その定義と位相的性質を解説しましょう。
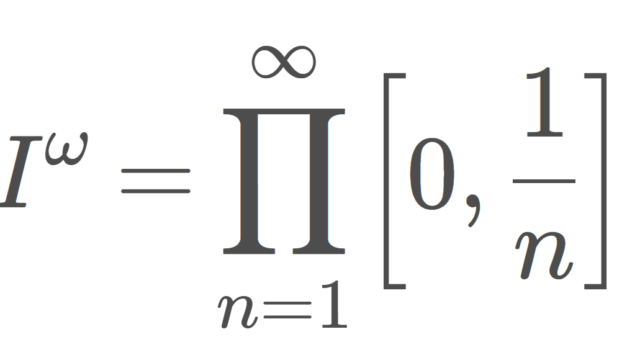 集合と位相
集合と位相  集合と位相
集合と位相 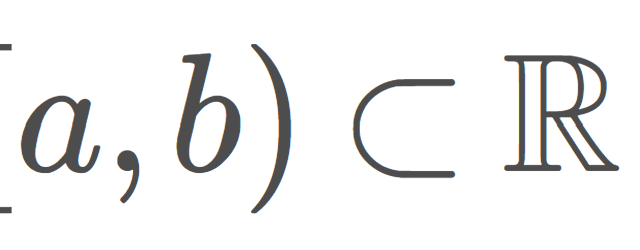 集合と位相
集合と位相 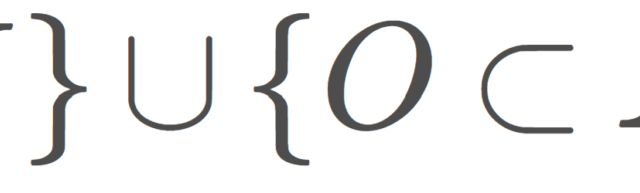 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 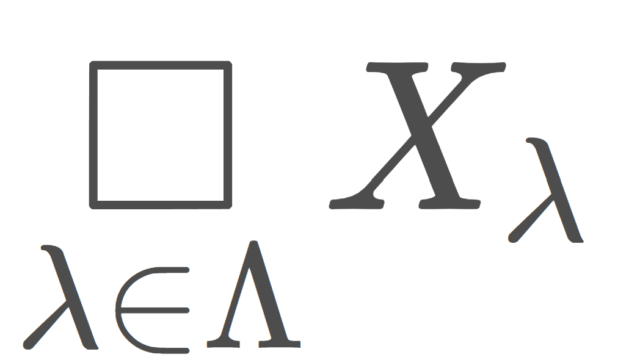 集合と位相
集合と位相