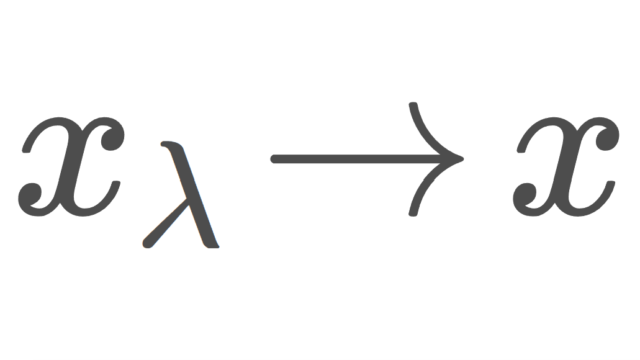 集合と位相
集合と位相 ネット(有向点族)による位相空間論と点列との比較
正の整数を添え字とする点列について,添え字をより一般の有向集合に変えたものをネットあるいは有向点族・有向点列といいます。一般の位相空間を扱うにあたって,点列では不十分であることが知られていますが,ネットであれば,一般の位相空間を特徴づけることができます。ネットについて,定義から位相の特徴づけまで,証明付きでかつ点列では不十分であることも確認しながら,進めていきましょう。
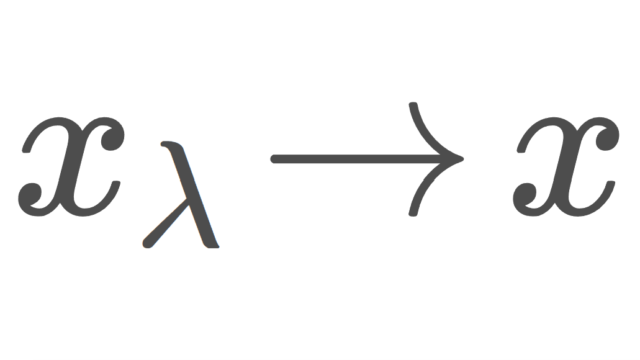 集合と位相
集合と位相 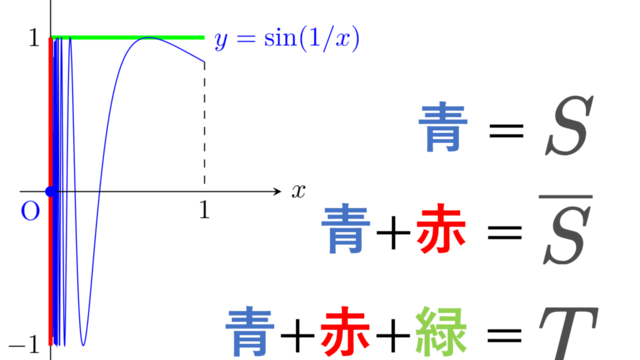 集合と位相
集合と位相 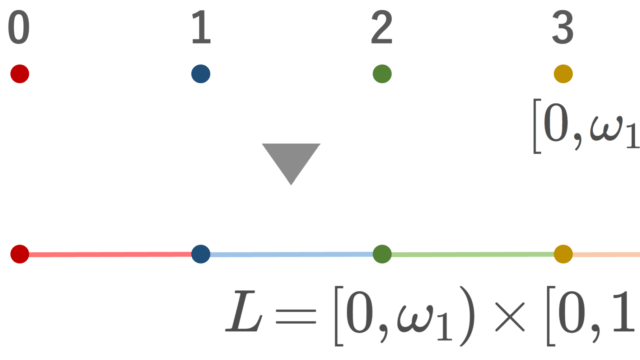 集合と位相
集合と位相 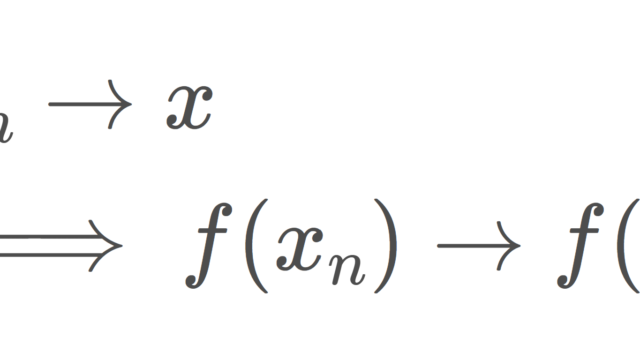 集合と位相
集合と位相 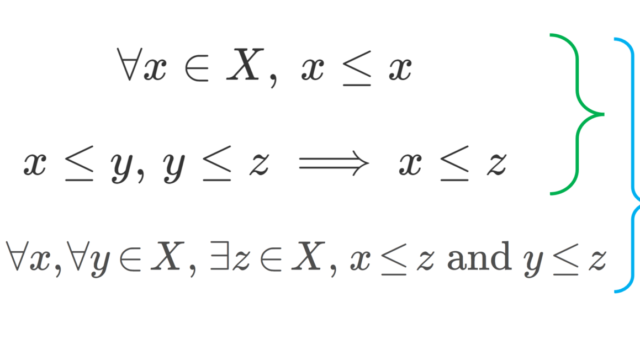 集合と位相
集合と位相 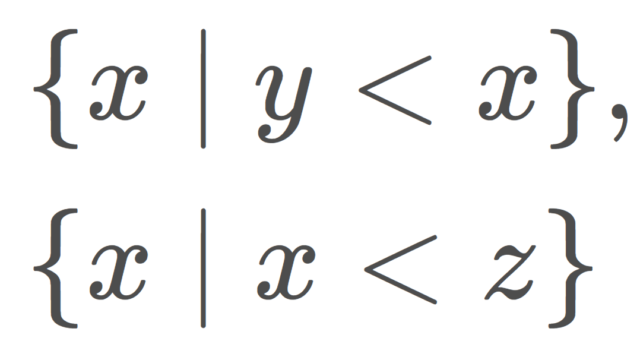 集合と位相
集合と位相 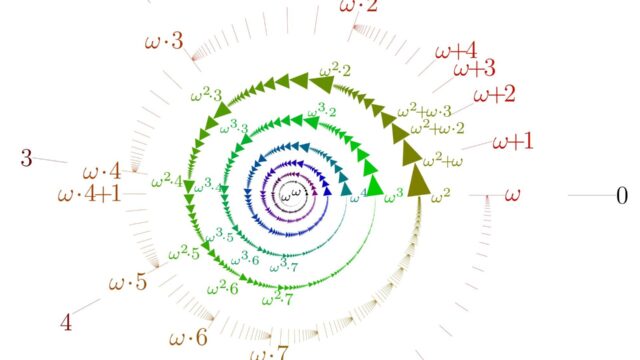 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 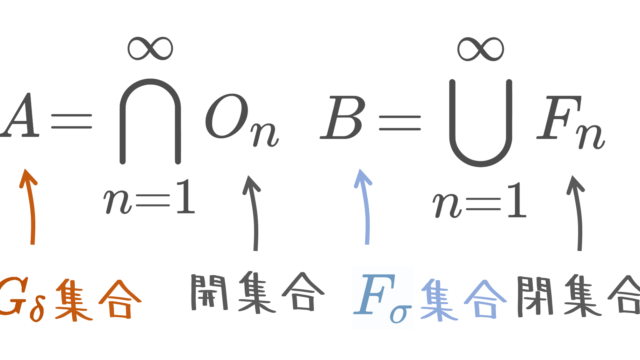 集合と位相
集合と位相