複素関数論 一般二項展開とそれを用いたマクローリン展開の例
高校数学で学ぶ二項定理による多項式の展開公式は，指数部分が正の整数の場合に限られていました。この指数を一般の複素数にまで拡張したものが一般二項展開です。この展開は，(1+z)^αにおけるマクローリン展開の表現にもなっています。一般二項展開の定義と，その具体例・証明について分かりやすく解説していきましょう。
大学専門
複素関数論 
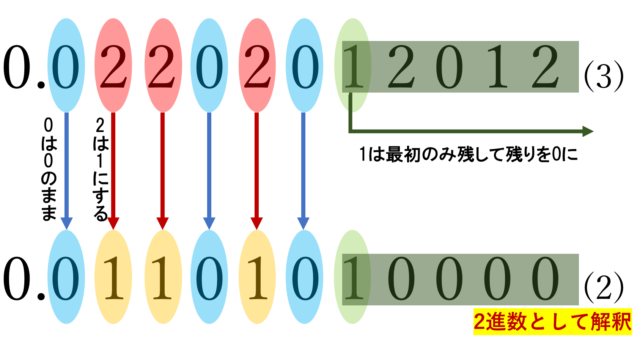
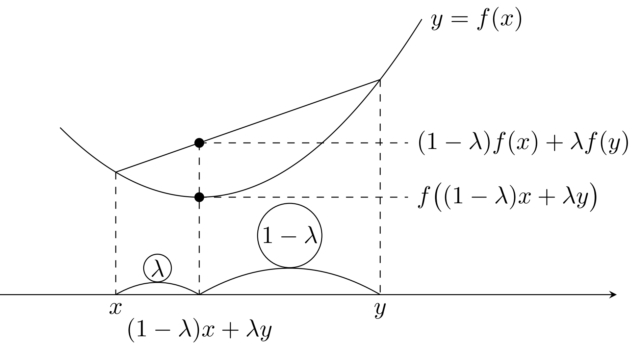
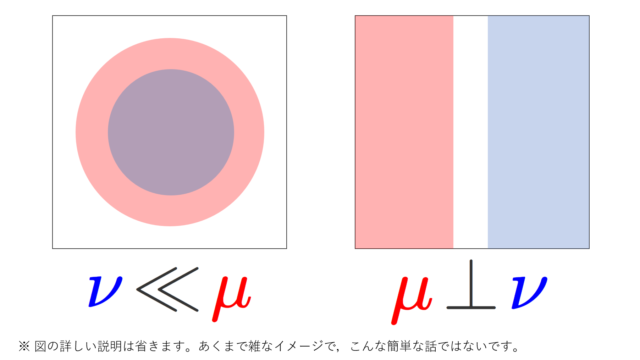
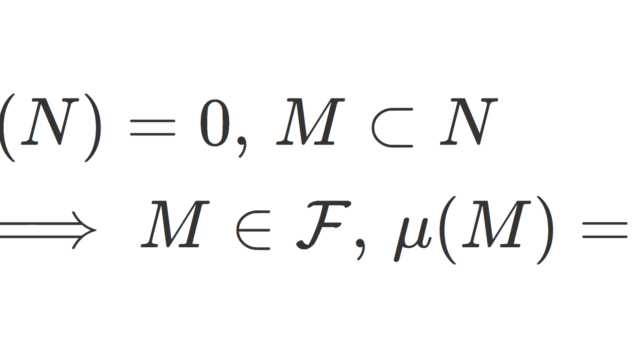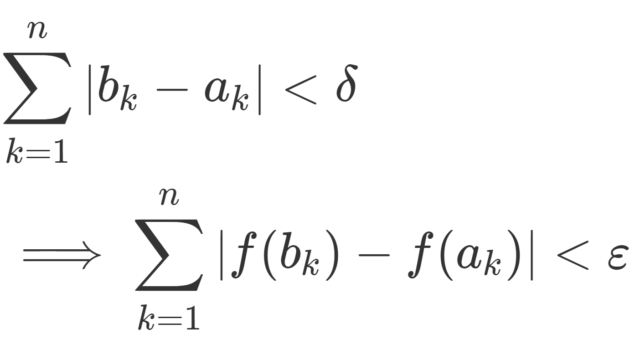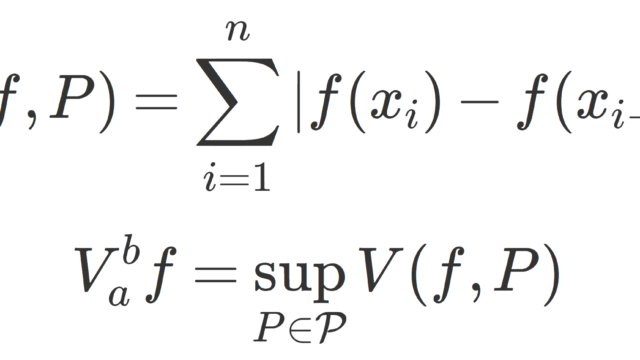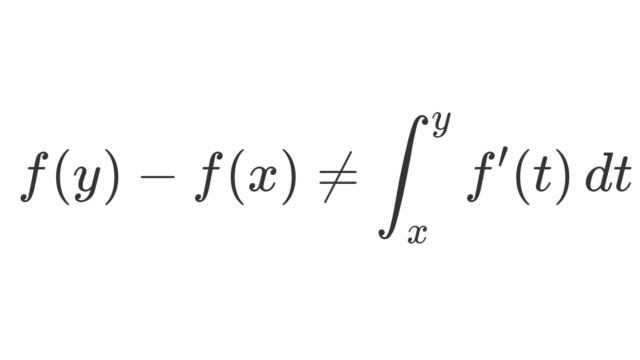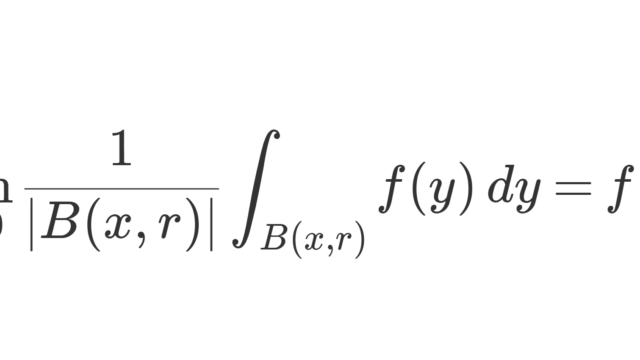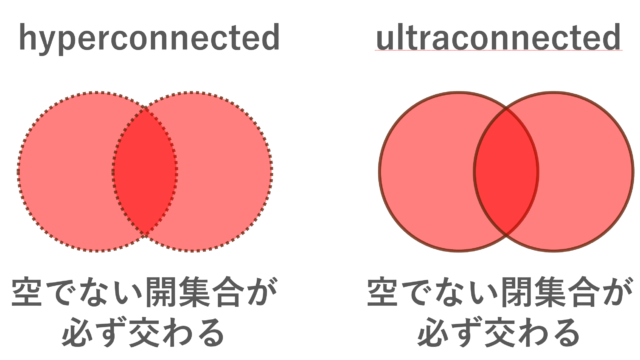
集合と位相 hyperconnected(既約位相空間)とultraconnected
hyperconnected な位相空間とは，任意の空でない2つの開集合が常に共通部分を持つ空間のことで，ultraconnected な位相空間とは，任意の空でない2つの閉集合が常に共通部分を持つ空間のことを言います。定義は似ていますが，別の空間で，hyperconnected だが ultraconnected でない空間や，その逆も考えられます。これらの空間について，定義と具体例，簡単な性質を紹介しましょう。
解析学(大学)その他 カントール関数のさまざまな定義とその重要な性質5つ
カントール関数 (Cantor function) とは，一様連続だが絶対連続でない関数の例の一つです。悪魔の階段ともいわれ，病的な関数として知られています。カントール関数を分かりやすく定義し，その性質を証明していきましょう。
測度論 完備な測度と測度空間の完備化
完備な測度空間とは，零集合の任意の部分集合が可測，従って零集合になる測度空間のことをいいます。任意の測度空間は完備な拡張を持つことが知られています。完備な測度と，任意の測度空間の完備化について紹介しましょう。
解析学(大学)その他 凸関数と凸不等式(イェンセンの不等式)についてかなり詳しく
凸関数 (convex function) は，それ自身が研究対象の一つであり，凸解析 (convex analysis) といわれることがあります。凸関数・凹関数と凸不等式（イェンセンの不等式）について，基本的なことを詳しくまとめましょう。
解析学(大学)その他 絶対連続な関数とは～定義と例と性質4つ～
絶対連続な関数とは，一様連続の定義をさらに厳しくしたような感じで，測度の絶対連続性の概念とも密接に関連しています。絶対連続性について，その定義・例・性質を紹介しましょう。
解析学(大学)その他 有界変動関数の定義と例といくつかの大事な性質
有界変動関数とは，「変動」つまり上下にどのくらい動くかが，「有界」すなわちそんなに変動しないということです。有界変動関数は，2つの単調増加関数の差で表すことができることが知られています。有界変動関数について，その定義と，大事な性質を証明付きで紹介していきましょう。
測度論 単調関数はほとんどいたるところ微分可能である証明
単調増加または単調減少関数，より一般に有界変動関数は，ほとんどいたるところ微分可能であることが知られています。これについて，ラドンニコディムの定理やルベーグの微分定理を用いた証明を紹介しましょう。
測度論 ルベーグの微分定理とその証明～測度の微分を添えて～
ルベーグの微分定理(Lebesgue differentiation theorem)は，リーマン積分のときに成り立っていた「積分して微分すると元に戻る」という性質の，ルベーグ積分版といえます。ルベーグの微分定理とその証明を行い，測度の微分について少し掘り下げましょう。
測度論 測度の絶対連続性・同値性・特異性とルベーグ分解
同じ可測空間に二つ測度があったときに，その二つの測度の関係性を述べるのが測度の絶対連続性・同値性・特異性です。また，任意のσ有限な測度は，別の測度に関して絶対連続なものと特異なものの和に分解できることが知られており，これをルベーグの分解定理といいます。測度の絶対連続性・同値性・特異性と，ルベーグの分解定理について，証明付きで紹介しましょう。