カントール関数のさまざまな定義とその重要な性質5つ

カントール関数とは，一様連続だが絶対連続でない関数の例の一つです。悪魔の階段ともいわれ，病的な関数として知られています。カントール関数を分かりやすく定義し，その性質を証明していきましょう。

カントール関数とは
カントール関数とカントール集合
折れ線近似を用いたカントール関数の定義
カントール関数の性質5つ
関連する記事

カントール関数とは

定義（カントール関数）

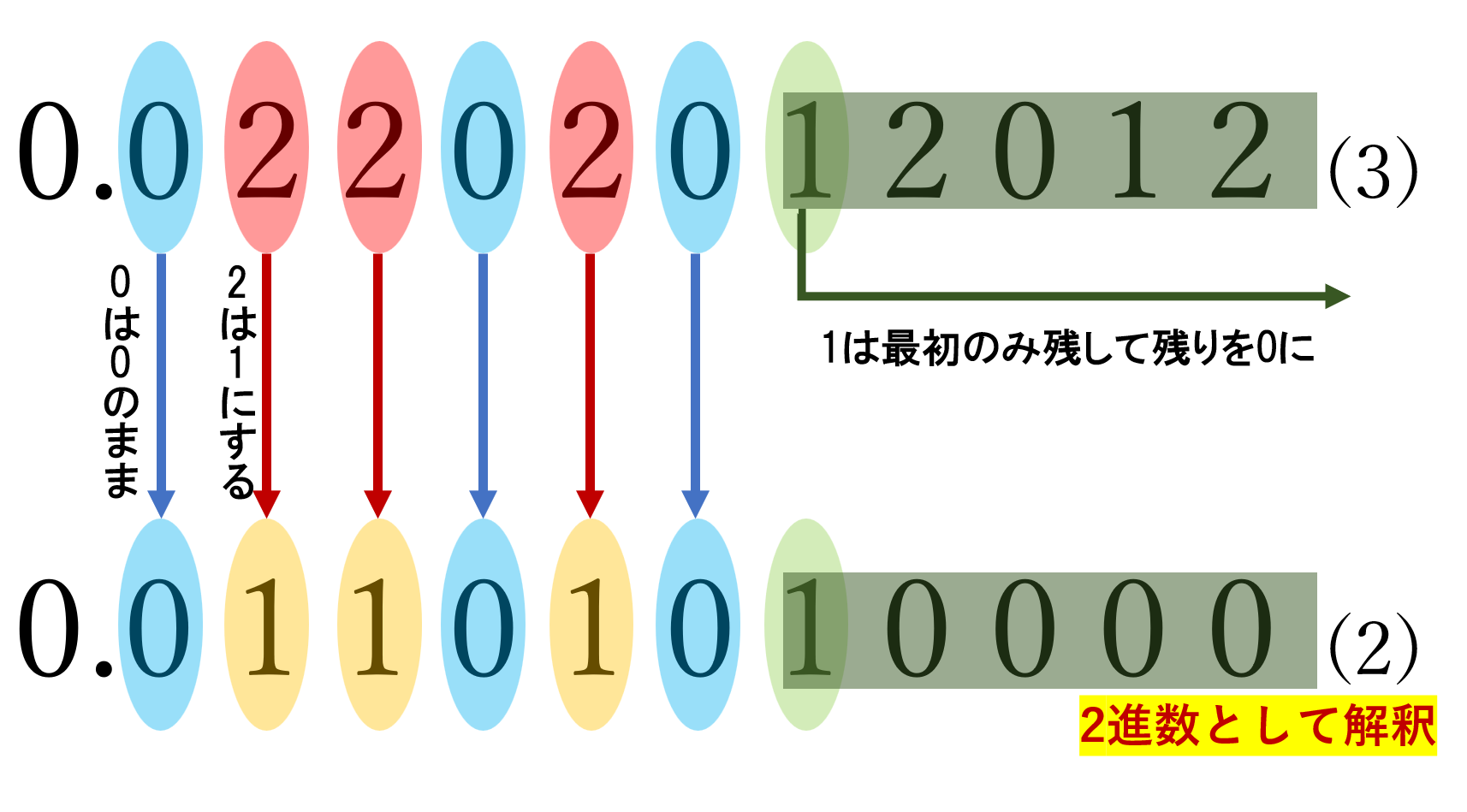
関数 $c\colon [0,1]\to [0,1]$ を以下のように定義する。

$x\in [0,1]$ を三進表示する。
$x$ の各位について， $0$ はそのままで， $2$ を $1$ に変える。 $1$ が出てきたらその $1$ のみ残し，それ以降の位を全て $0$ にする。
2で得た小数を二進表示と解釈して， $c(x)$ の値とする。

このような関数 $c$ をカントール関数 (Cantor function) という。

以下の図が分かりやすいと思います。

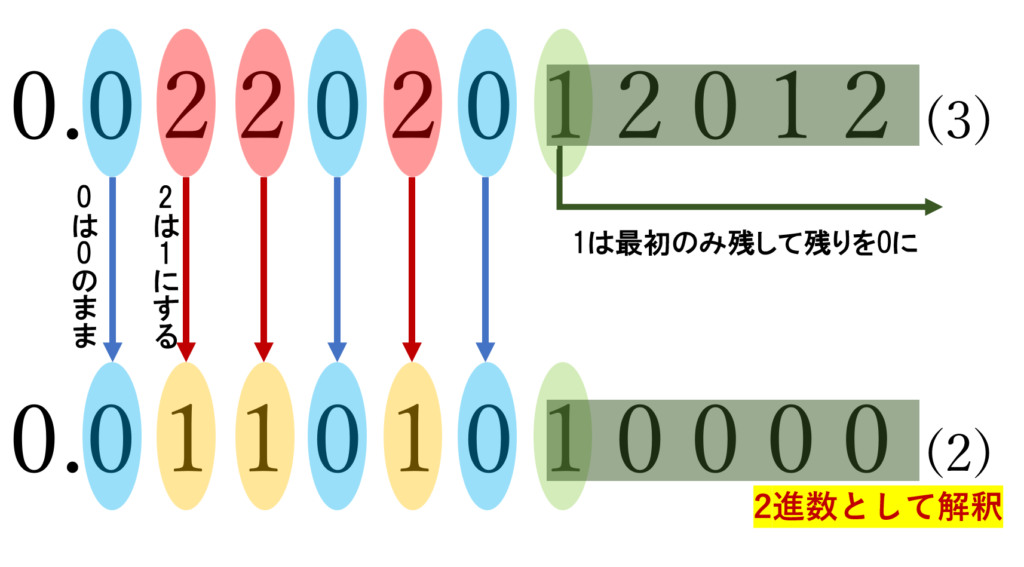
ここで，たとえば $0.1_{(3)}=0.0222\dots_{(3)}$ ですが，これに対応するのは $0.1_{(2)}=0.0111\dots_{(2)}$ となっているため，この変換は小数表示の仕方に依らず，well-definedです。

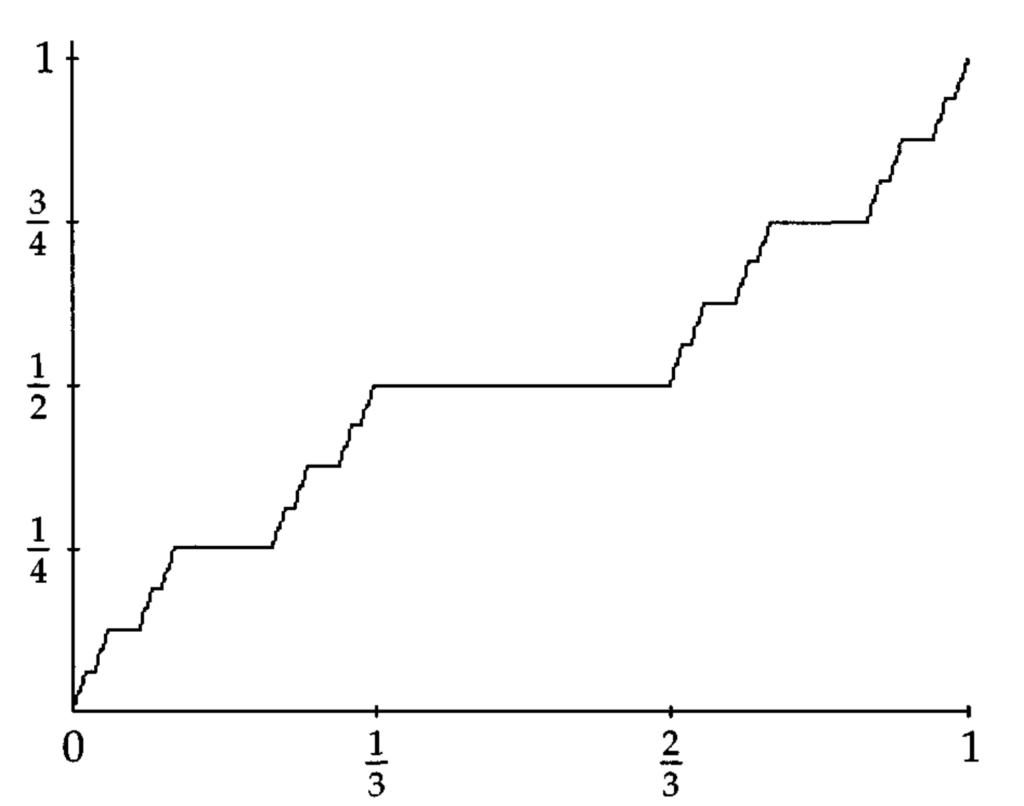
この手順に基づくと，例えば $c(1/3)=c(1/2)=1/2, \, c(2/9)=1/4$ ですね。カントール関数のグラフを厳密にかくことはできませんが，おおよそのイメージは以下のような感じです。

カントール関数とカントール集合

カントール関数とカントール集合は，大いに関係性があります。まずはカントール集合とは何か確認しておきましょう。

カントール集合

$[0,1]$ のうち，三進数で表示したときに $1$ が出てこないようにすることができる数の集合 $\mathscr{C}$ をカントール集合 (Cantor set) という。ただし，たとえば $0.1_{(3)}= 0.0222\dots_{(3)}\in\mathscr{C}$ と解釈する。具体的には，

\color{red} \mathscr{C}=\left\{\sum_{n=1}^\infty\frac{2a_n}{3^n}\middle| a_n =0,1\right\}

と表せる。カントール集合は，連続体濃度を持つ，ルベーグ測度 $0$ の閉集合である(→カントール集合の定義と性質3つの証明)。

カントール集合は以下のように，各区間を3等分して，真ん中の開区間をくり抜くことを無限回繰り返すことで得られる集合です。

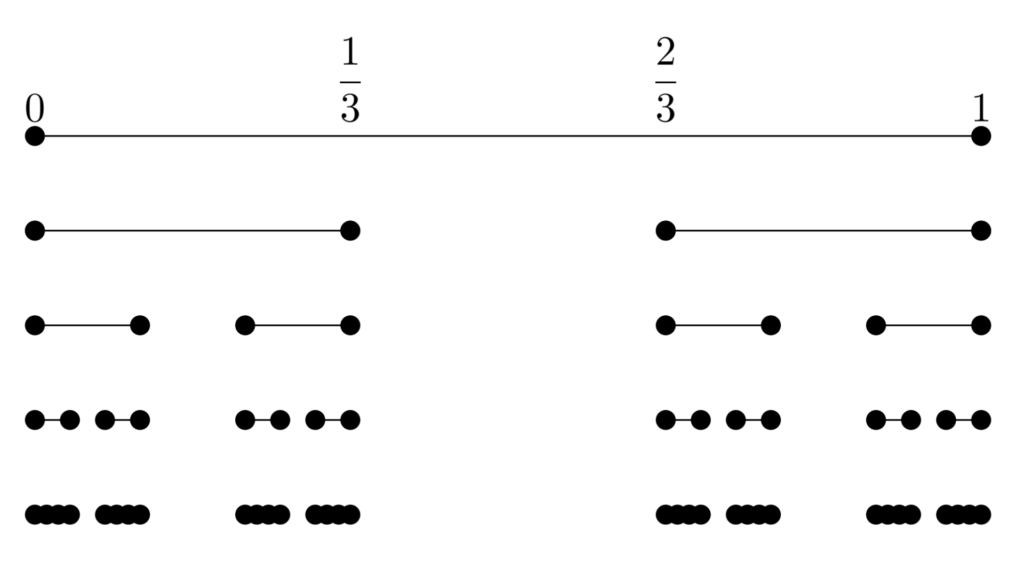
この見方をすると，カントール集合は

\color{red}\mathscr{C}= [0,1]\setminus \bigcup_{n=1}^\infty \bigcup_{k=0}^{3^{n-1}-1} \left( \frac{3k+1}{3^n},\frac{3k+2}{3^n}\right)

とかけます。カントール集合について詳しくはカントール集合の定義と性質3つの証明で解説しています。カントール集合を用いると，カントール関数は以下のようにかくことができます。

カントール集合を用いたカントール関数の定義

$\mathscr{C}\subset [0,1]$ をカントール集合とする。 $c\colon [0,1]\to [0,1]$ を以下のように定める。

$\displaystyle \color{red} c\left(\sum_{n=1}^\infty \frac{2a_n}{3^n} \right)= \sum_{n=1}^\infty \frac{a_n}{2^n},\quad a_n=0, 1$
$\color{red}c(y)= \sup\{c(x)\mid x\le y, \, x\in \mathscr{C}\}$

このとき， $c$ はカントール関数である。

1.で $c\colon \mathscr{C}\to [0,1]$ を定義し，2.でその定義域を $[0,1]$ に拡張しています。

$\displaystyle \sum_{n=1}^\infty \frac{2a_n}{3^n},\; a_n=0,1$ は，三進数表示をしたときに，小数第 $n$ 位が $2a_n$ になる数で， $\displaystyle \sum_{n=1}^\infty \frac{a_n}{2^n}$ は二進数表示したときに，小数第 $n$ 位が $a_n$ になる数です。よって，冒頭の定義と，今回の定義が対応していることが分かると思います。

上の定義の形からもわかるように，カントール関数は，上図でカントール集合の構成の際にくり抜かれた各開集合上では定数になります。カントール関数のグラフの概形を再掲します。たしかに， $(1/3, 2/3), (1/9,2/9), (7/9,8/9),\dots$ ではグラフが $x$ 軸に平行になっていますね。

折れ線近似を用いたカントール関数の定義

折れ線近似を用いた，カントール関数の別の定義を紹介しましょう。

定理1（カントール関数の折れ線近似による定義）

関数列 $\{f_n\colon [0,1]\to [0,1]\}$ を次のように定める。

\begin{aligned} f_0(x)&=x, \\ f_{n+1}(x)&= \begin{dcases} \frac{1}{2}f_n(3x) & 0\le x<\frac{1}{3},\\[10pt] \frac{1}{2} & \frac{1}{3}\le x<\frac{2}{3},\\[10pt] \frac{1}{2}+\frac{1}{2}f_n(3x-2) & \frac{2}{3}\le x\le 1 \end{dcases} \end{aligned}

このとき， $\{f_n\}$ はカントール関数 $c$ に一様収束する。

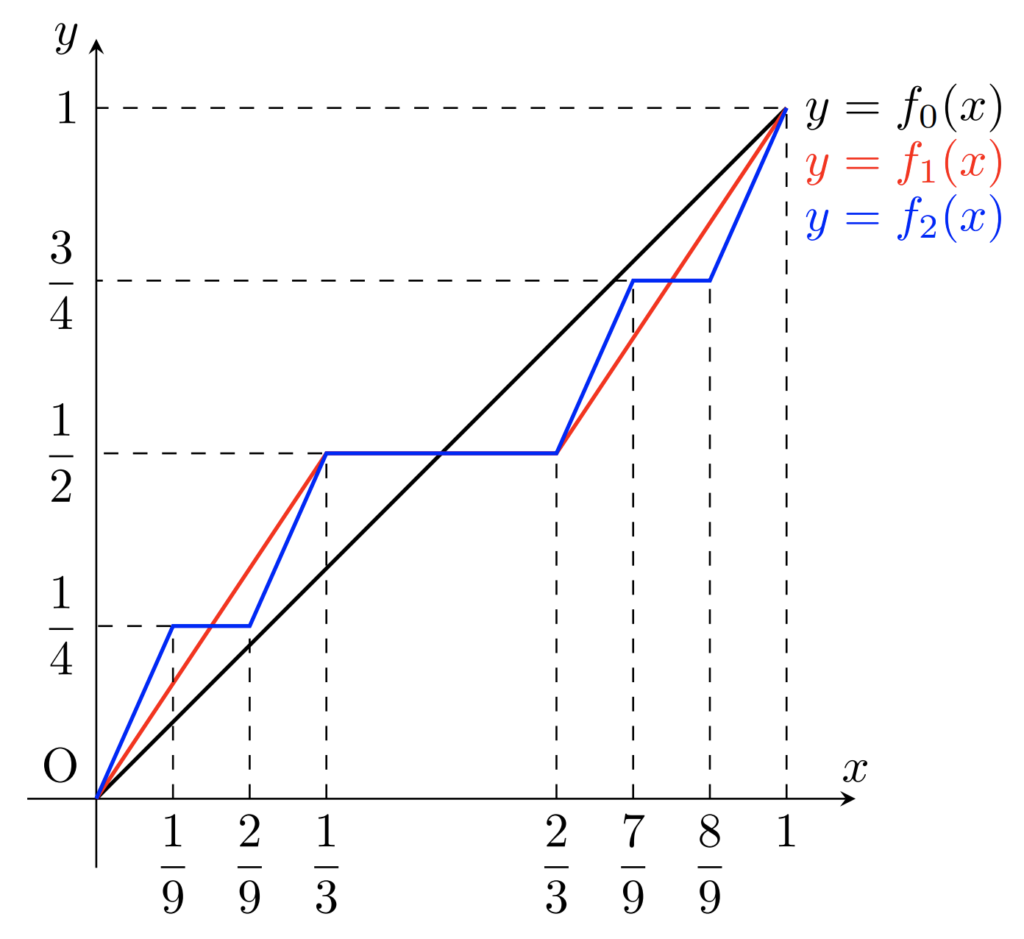
証明

\small \begin{aligned}&f_{n+1}(x)-f_n(x) \\&= \begin{dcases} \frac{1}{2}\{f_n(3x) -f_n(3x)\}& 0\le x<\frac{1}{3},\\[5pt] 0 & \frac{1}{3}\le x<\frac{2}{3},\\[5pt] \frac{1}{2}\{f_n(3x-2) -f_{n-1} (3x-2)\}& \frac{2}{3}\le x\le 1 \end{dcases}\end{aligned}

であるから，

\begin{aligned}&\max_{0\le x\le 1} |f_{n+1}(x)-f_n(x)|\\&\le \frac{1}{2} \max_{0\le x\le 1} |f_{n}(x)-f_{n-1}(x)|\end{aligned}

である。帰納的に用いると，

\begin{aligned}&\max_{0\le x\le 1} |f_{n+1}(x)-f_n(x)|\\&\le 2^{-n}\max_{0\le x\le 1} |f_1 (x)-f_{0}(x)|\end{aligned}

を得る。よって， $1<m<n$ に対し，

\begin{aligned}|f_n(x)-f_m(x)| &\le \sum_{i=m}^{n-1} |f_{i+1}(x)-f_i(x)| \\&\le \sum_{i=m}^{n-1}\max_{0\le x\le 1} |f_{i+1}(x)-f_i(x)| \\&\le \sum_{i=m}^{n-1} 2^{-i} |f_1(x)-f_0(x)| \\&\le 2^{-m+1} |f_1(x)-f_0(x)| \end{aligned}

が成り立つため， $\{ f_n\}$ は一様コーシー列である。ゆえに，ある関数 $f$ に一様収束する。 $f$ がカントール関数であることは，証明直前の図を考えて(厳密には $x$ を三進表示し， $f_n(x)$ を二進表示して $c(x)$ の二進表示と比較することで)，

|f_n (x)-c(x)|\le 2^{-n} \xrightarrow{n\to\infty} 0

となることからわかる。

[証明終

カントール関数の性質5つ

カントール関数は不思議な性質を持ちます。見ていきましょう。

定理2（カントール関数の性質）

$c\colon [0,1]\to [0,1]$ をカントール関数とする。

$c$ は広義単調増加で全射である。よって，有界変動関数である。
$c$ は一様連続である。
$c$ はほとんどいたるところ微分可能で， $c'(x)=0,\,\text{a.e.}$ である。
$c$ は絶対連続ではない。とくに，特異関数である。
$c$ は $\log 2/\log 3$ -ヘルダー連続である。

カントール関数は悪魔の階段 (devil’s staircase) と呼ばれることがありますが，それは，上の2.から4.にかけての，一見すると矛盾するような性質を持つからです。また，連続なのに絶対連続でないという意味で特異関数 (singular function) の一種といわれることもあります。

証明

1. $c$ の広義単調増加性は定義より明らか。また，全射性も各二進数に対応する，もとの三進数を作れるので明らか。

2. $c$ の一様連続性について

$c$ が $x\in [0,1]$ で連続でないと仮定する。 $c$ は広義単調増加なので，

\lim_{y\to x-} f(y)< \lim_{y\to x+} f(y)

である。左辺を $f(x-)$ ，右辺を $f(x+)$ とかく。このとき， $(f(x+), f(x-))\setminus \{ f(x)\}$ は $f$ の値域に入らなくなってしまうが，これは $f$ の全射性に矛盾する。よって $f$ は連続であり，有界閉区間上連続な関数は一様連続なので，題意は示された。

あるいは，カントール関数は連続関数の一様収束極限（折れ線近似）で得られたことと，連続関数列の一様収束極限は必ず連続関数になることの証明より，カントール関数は連続と言っても良い。

3. $c'(x)=0,\,\text{a.e.}$ について

開集合 $[0,1]\setminus \mathscr{C}$ の各点の近傍では定数関数なので， $x\in[0,1]\setminus \mathscr{C}$ で $c'(x)=0$ である。ここで，カントール集合 $\mathscr{C}$ は零集合である(→カントール集合の定義と性質3つの証明)から，示された。

4. $c$ が絶対連続でないことについて

$c$ が絶対連続とすると，絶対連続な関数とは～定義と例と性質4つ～より，