デデキント切断をざっくり説明すると,有理数のみの数直線を2つに切断して,その「切り口」を新たに数と思うことで,実数を定義しようというものです。これにより,有理数にはない「実数の連続性」が成り立ちます。
デデキント切断について,その定義から実数の定義を紹介し,さらに実数の連続性について述べ,実数の演算を定義していきましょう。
デデキント切断から実数の定義へ
まずデデキント切断の定義と具体例を述べ,実数の定義へと入っていきます。
デデキント切断とは
まずは,デデキント切断を用いて,有理数から実数を定義していきましょう。当たり前ですが,実数を知らない(有理数しか知らない)世界の人視点で実数を定義しますから,定義に実数を使ってはいけません。
定義1(デデキント切断)
有理数全体の集合 \mathbb{Q} におけるデデキント切断 (Dedekind cut) とは,以下をみたす集合の組 (A,B) のことである。
- \large\color{red} A\cup B=\mathbb{Q},\,\, A, B\ne \emptyset,\,\, A\cap B=\emptyset,
- \large \color{red} a\in A,\, b\in B\implies a< b.
- A には最大値が存在しない。
本記事では,この切断を \color{red} \large A\mid B とかくことにする。
1.より, B=\mathbb{Q}\setminus A です。 \mathbb{Q} を,共通部分を持たない二つの空でない集合に分けているわけですね。そして2.より,二つの集合は大小が「はっきり」分かれている(混ざりあっていない)ことを意味しています。また,3.がある理由は,今回大事なのは切断部分の切り口であって,たとえば
(-\infty, 2]\mid (2,\infty) と (-\infty, 2)\mid [2,\infty)
という,切り方の違う二つを区別したいわけではないので,後者に統一してしまおうというわけです(ただし,上の区間は全て有理数の範囲のみで考える。すなわち, (-\infty, 2], (2,\infty),(-\infty, 2),[2,\infty)\subset\mathbb{Q} で考える)。なお,「 A に最大値が存在しない」の部分を,「B に最小値が存在する」と言い換えることはできません。「切り口」が有理数でないときは, A, B\subset \mathbb{Q} ともに最大値・最小値は存在しません。
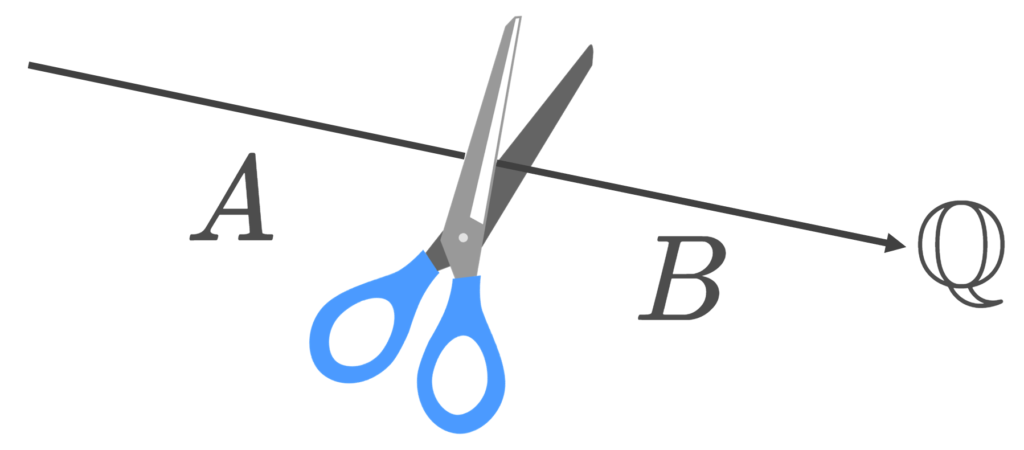
デデキント切断のイメージ図として,上のようなものが用いられることがありますし,概ね間違っていません。ただ,切っているのはあくまで(我々が知っている, \mathbb{R} を表す)数直線ではなく, \mathbb{Q} であることに注意してください。そして,後で定義しますが,有理数全体の集合に,切り口を全て補完したものが実数です。
有理数ではなく,一般の全順序集合においてデデキント切断を定義することもありますが,そのときは3.を除くことが多いです。
デデキント切断の具体例
実数を定義する前に,デデキント切断の具体例をいくつか挙げましょう。注意ですが,定義の前に述べたとおり,我々はまだ実数を知りませんから,切断に実数を使わないことにします。
例1.
\begin{aligned}A&= \{q\in\mathbb{Q}\mid q<2\},\\ B&= \{q\in\mathbb{Q}\mid 2\le q\} \end{aligned}
により定められる A\mid B はデデキント切断である。
\color{red} (-\infty, 2)_\mathbb{Q}\mid [2,\infty)_\mathbb{Q} ということですね。上でも述べましたが,本記事においては, (-\infty, 2]_\mathbb{Q} \mid (2,\infty)_\mathbb{Q} はデデキント切断ではありません。
例2.
\begin{aligned}A&= \{q\in\mathbb{Q}\mid q\le 0\text{ or } q^2<2\},\\ B&= \{q\in\mathbb{Q}\mid q>0\text{ and }2\le q^2\} \end{aligned}
により定められる A\mid B はデデキント切断である。
実数を使って表すなら,\color{red} (-\infty, \sqrt{2})_\mathbb{Q}\mid [\sqrt{2},\infty)_\mathbb{Q} ということですね。
\sqrt{2}\not\in \mathbb{Q} ですから,今回のデデキント切断 A\mid B における A, B はそれぞれ最大値・最小値は存在せず, (-\infty, \sqrt{2})_\mathbb{Q}\mid (\sqrt{2},\infty)_\mathbb{Q} や (-\infty, \sqrt{2}]_\mathbb{Q}\mid [\sqrt{2},\infty)_\mathbb{Q} などとかいても同じことです。
例3.
\begin{aligned}A&= \left\{q\in\mathbb{Q}\mid \exists n\ge 1, q< \left(1+\frac{1}{n}\right)^n \right\},\\ B&= \mathbb{Q}\setminus A\end{aligned}
により定められる A\mid B はデデキント切断である。
実数を使って表すなら,\color{red} (-\infty, e)_\mathbb{Q}\mid [e,\infty)_\mathbb{Q} ということですね。ただし, e は自然対数の底(ネイピア数)です。 n\mapsto (1+1/n)^n は単調増加で, e に収束することに注意してください。
デデキント切断から実数へ
さて,デデキント切断を用いて実数を定義しましょう。
定義2(デデキント切断を用いた実数の定義)
デデキント切断 A\mid B 全体の集合を \large\color{red}\mathbb{R} とかき,実数全体の集合 (a set of real numbers) という。 \mathbb{R} における各デデキント切断 A\mid B\in \mathbb{R} を実数 (real number) という。
各デデキント切断そのものを実数と見るわけですね。
ただし, B に最小値 b が存在する場合,すなわち「切り口」が有理数 b の場合は, デデキント切断 (-\infty, b)_\mathbb{Q}\mid [b, \infty)_\mathbb{Q} \in\mathbb{R} のことを単に b\in \mathbb{R} とかくことにします。すなわち 有理数 b\in\mathbb{Q} と切断 (-\infty, b)_\mathbb{Q}\mid [b, \infty)_\mathbb{Q} \in\mathbb{R} を同一視します。これにより,\mathbb{Q}\subset \mathbb{R} とみなします。実数を有理数の拡張とみるわけですね。「大事なのは切り口」と言ってきたのはこういうことです。
実数の連続性(sup, infの存在定理)
実数の連続性を表す定理の一つである,上限(sup)・下限(inf)の存在定理について述べましょう。そのまえに実数に順序関係を定めねばなりません。
構成した実数に順序関係を定める
定義3(実数における順序関係)
x=A_1\mid B_1, \, y= A_2\mid B_2\in\mathbb{R} とする。このとき,
- A_1\subset A_2 のとき \color{red} x\le y とし,
- A_1\subsetneq A_2 のとき \color{red} x<y とする。
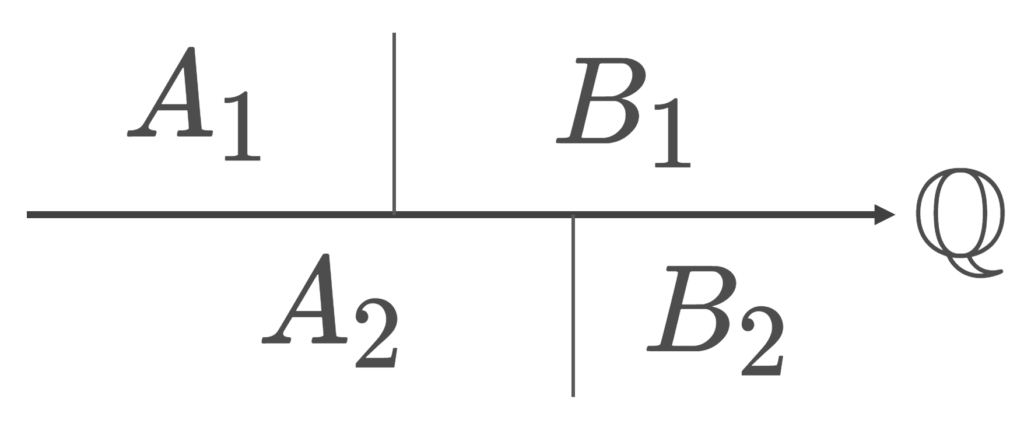
これは全順序になっています。つまり, x,y\in\mathbb{R} に対し, x\le y または y\le x のいずれかが成立します。実際,もし x=A_1\mid B_1,\, y=A_2\mid B_2 に対し, A_1\subset A_2,\, A_2\subset A_1 のいずれも成立しないとすると, q\in A_1\setminus A_2,\, q' \in A_2\setminus A_1 が取れますが,デデキント切断 A_1\mid B_1 の定義より q<q' となり, A_2\mid B_2 の定義より q'<q になって \mathbb{Q} の全順序性に矛盾します。
これを踏まえて,実数の連続性を述べ,証明しましょう。
実数の連続性(sup, infの存在定理)
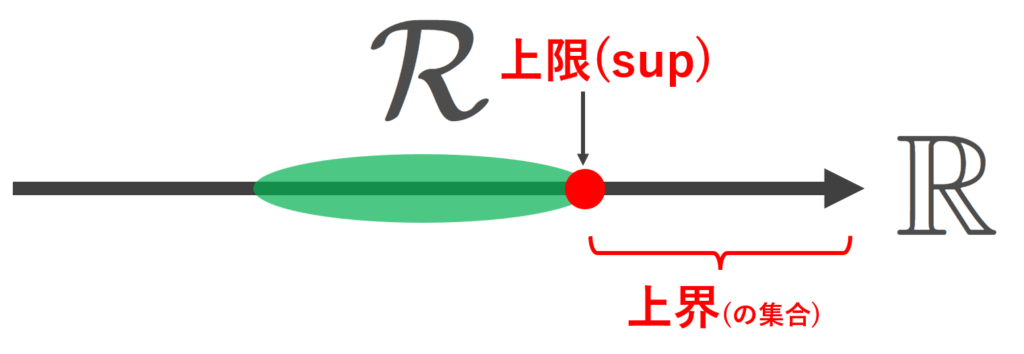
定理(実数の連続性; \sup,\inf の存在)
\mathcal{R}\subset \mathbb{R} は空でなく,上に有界であるとする。すなわち,ある M\in \mathbb{R} が存在して,
r\le M \quad (\forall r\in \mathcal{R})
が成立すると仮定する(このような M を上界 (upper bound) という)。
このとき, \mathbb{R} において,\mathcal{R} の最小上界(上限 (supremum) という) M_0 が存在する(この M_0 を \large\color{red}\sup \mathcal{R} とかく)。すなわち M_0 は上界であるが, M'<M_0 をみたす任意の M'\in\R は上界でないような M_0 が存在する。
同様に最小下界(下限)も考えることができる。
一般の順序集合における上界・上限などは半順序集合・全順序集合の定義・具体例4つとその周辺で解説しています。
証明しましょう。
証明
\begin{aligned} C&= \bigl\{ q\in \mathbb{Q}\bigm| \exists A \mid B\in\mathcal{R}, q\in A\bigr\}, \\ D&= \mathbb{Q}\setminus C \end{aligned}
とする。 \mathcal{R} は上に有界なので, D\ne \emptyset に注意する。 z=C\mid D はデデキント切断であることは簡単にわかるから, z\in\mathbb{R} である。 z=\sup \mathcal{R} を示そう。
まず,任意の x= A\mid B\in\mathcal{R} について A\subset C であるから, x\le z なので, z は \mathcal{R} の上界の一つである。さらに, z'=C'\mid D' を \mathcal{R} の任意の上界とすると,任意の x= A\mid B\in\mathcal{R} について x\le z' なので, A\subset C' となるから, C\subset C' である。ゆえに z\le z' なので, z は最小上界すなわち上限である。
証明終
なお,逆に実数の連続性を認めると,デデキント切断 A\mid B は r=\sup A\in\mathbb{R} とすることで,単に (-\infty, r)_\mathbb{Q}\mid [r, \infty)_\mathbb{Q} とかくことができます。
実数の連続性が関係する記事
他にも,以下の記事は実数の連続性が深く関係しています。列挙しておきましょう。
特に,3つ目は実数におけるコーシー列は収束する定理を紹介しており,実数の連続性(完備性)というと,この定理を指すことも多いです。
その証明には,上2つの記事を使っていますが,上に有界な単調増加数列は収束することは,先ほど紹介した \sup, \inf の存在定理を用いています。
実数における演算の定義

デデキント切断によって構成した実数に四則演算を定義しておきましょう。有理数の四則演算は既に定義されているものとします。
定義4(実数同士の和)
x= A\mid B, \, y=C\mid D\in\mathbb{R} とする。このとき,
\begin{aligned} E&= \{q\in\mathbb{Q}\mid \exists a\in A, \exists c\in C, q=a+c\},\\ F&= \mathbb{Q}\setminus E \end{aligned}
と定めたデデキント切断 E\mid F\in\mathbb{R} を \large\color{red} x+y とかき,これを x と y の和 (sum) という。
x,y,z\in\mathbb{R} に対し,明らかに x+y=y+x,\, (x+y)+z=x+(y+z) です。また, 0=(-\infty, 0)_\mathbb{Q}\mid [0,\infty)_\mathbb{Q}\in\mathbb{R} について, x+0=0+x=x もわかります。
また, x,y,z\in\mathbb{Q} のとき, \mathbb{R} と \mathbb{Q} の演算は矛盾しておらず, \R の演算は \mathbb{Q} の演算の拡張になっていることも分かります。
次に, x\in\mathbb{R} に対し, -x\in\mathbb{R} を定義することで,差を定義します。
定義5(実数の加法逆元・差)
x= A\mid B, \, y=C\mid D\in\mathbb{R} とする。このとき,
\begin{aligned} E&= \{-b\in\mathbb{Q}\mid b\in B\setminus \min B \},\\ F&= \mathbb{Q}\setminus E \end{aligned}
と定めたデデキント切断 E\mid F\in\mathbb{R} を \large\color{red} -x とかき,これを x の加法逆元 (additive inverse) という。
また,これを用いて x と y の差 (difference) \large\color{red} x-y を x-y=x+(-y) で定義する。
x-x=0 となることや, -(-x))=x や x>0 \iff -x<0 となることが容易に確認できます。
積についての定義は少々やっかいです。 x,y\in\mathbb{R} の正負,すなわち x,y\gtrless 0 によって定義が変わります。
定義6(実数の積)
x= A\mid B, \, y=C\mid D\in\mathbb{R} とする。
1. x,y>0 のとき
\begin{aligned} E&=\left\{q\in\mathbb{Q}\mid q\le 0\text{ or }\begin{gathered}\exists a\in A,\exists c\in C, \\ a,c>0 , q=ac \end{gathered} \right\},\\ F&= \mathbb{Q}\setminus E \end{aligned}
と定めたデデキント切断 E\mid F\in\mathbb{R} を \large\color{red} xy とかき,これを x と y の積 (multiplication) という。また,これを用いて
2. x<0,\, y>0 のとき xy=-((-x)y)
3. x>0,\, y<0 のとき xy=-(x(-y))
4. x,y<0 のとき xy=(-x)(-y)
5. x=0 または y=0 のとき xy=0
と定義する。
少々面倒ですが, x,y,z\in\mathbb{R} に対し, xy=yx や x(y+z)=xy+xz,\, x\cdot 1=1\cdot x=x,\, (-1)x=-x などを確認することが可能です。
商の定義は,逆数を定義することで可能です。これも少々面倒です。
定義7(実数の乗法逆元・商)
x= A\mid B, \, y=C\mid D\in\mathbb{R} とする。
1. x>0 のとき
\begin{aligned} E&=\left\{q\in\mathbb{Q}\mid q\le 0\text{ or }\begin{gathered}\exists b\in B\setminus \min B,\\ q=1/b \end{gathered} \right\},\\ F&= \mathbb{Q}\setminus E \end{aligned}
と定めたデデキント切断 E\mid F\in\mathbb{R} を \large\color{red} 1/x とかき,これを x の乗法逆元 (multiplicative inverse) という。また,これを用いて
2. x<0 のとき 1/x=-(1/(-x))
と定義する。これを用いて, x\ne 0 と y の商 (quotient) \large\color{red} y/x を y/x=(1/x)y で定義する。
x( 1/x)=1 となることが確認できるはずです。