区間縮小法の原理とは,単調減少な閉区間の列の幅が 0 に収束するならば,閉区間は最後は1点に収束するという定理です。区間縮小法の原理は,実数の連続性が深く関係しています。
区間縮小法の原理について,実数の連続性を認めて証明し,逆に区間縮小法の原理から実数の連続性を導くこともできるため,それも紹介します。
区間縮小法の原理とその証明
区間縮小法の原理の定理の主張を述べ,それを証明していきましょう。
区間縮小法の原理の主張
定理1(区間縮小法の原理)
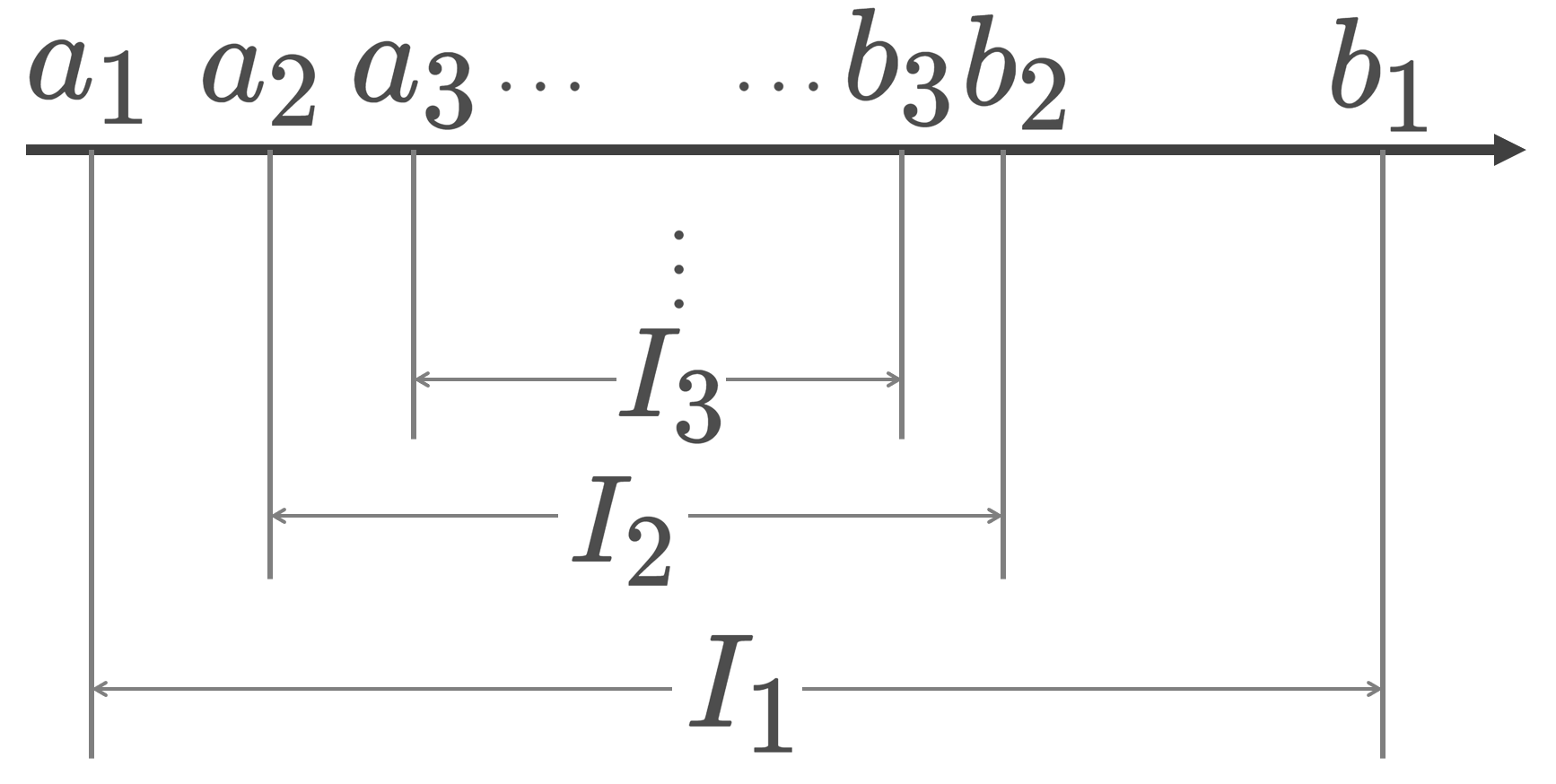
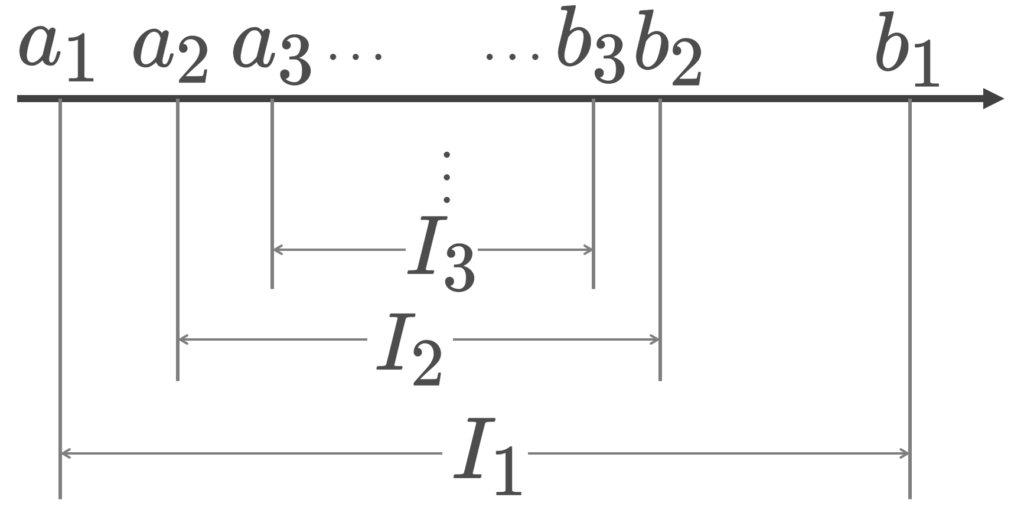
I_n = [a_n, b_n] を閉区間とし, I_1\supset I_2\supset I_3\supset \cdots とする。このとき,
\Large \color{red} \bigcap_{n=1}^\infty I_n \ne \emptyset
である。さらに, \lim_{n\to\infty} (b_n-a_n)=0 とすると,ある c\in \R が存在して,
となる。
I_1\supset I_2\supset I_3\supset \cdots を a_n, b_n を用いてかき直すと,
a_1\le a_2\le a_3\le \cdots \,\cdots \le b_3\le b_2\le b_1
となります。
当たり前のように思えるかもしれませんが,これは実数の連続性が深く関係しています。というのも,有理数のみに制限して考えると,これは成り立ちません。たとえば,
I_n = \left[ \frac{\lfloor 10^n \sqrt{2}\rfloor}{10^n},\frac{\lfloor 10^n \sqrt{2}\rfloor+1}{10^n} \right]\textcolor{red}{\boldsymbol{{} \cap \mathbb{Q}}}
とすると(ただし, \lfloor 10^n \sqrt{2}\rfloor は 10^n \sqrt{2} の整数部分を表す), \bigcap_{n=1}^\infty I_n = \emptyset となってしまいます。
また, I_n = (a_n, b_n) のように開区間にするとうまくいきません。たとえば,
\bigcap_{n=1}^\infty \left( 0, \frac{1}{n}\right) =\emptyset
です。ただし, \{a_n\} , \{b_n\} をそれぞれ狭義単調増加・狭義単調減少と仮定すると,上のような例はなくなり,定理が適用できます。たとえば,
です。
実数の連続性を用いた区間縮小法の原理の証明
実数の連続性を認めて,定理を証明していきましょう。
証明
\{a_n\} は上に有界な単調増加数列, \{b_n\} は下に有界な単調減少数列なので,それぞれ
\lim_{n\to\infty} a_n=\alpha, \quad \lim_{n\to\infty} b_n=\beta
となる \alpha, \beta\in\R が存在する(実数の連続性: 上に有界な単調増加数列は収束することの証明)。 a_n<b_n より, \alpha\le \beta である。したがって,
である。特に, \lim_{n\to\infty} (b_n-a_n)=0 とすると, \beta-\alpha=0 すなわち \alpha=\beta であり,これを新たに c とおくと, [\alpha, \beta] =\{c\} となって結論を得る。
証明終
実数の連続性に関係する話題
本記事では実数の連続性を用いて,区間縮小法の原理を証明しました。実数の連続性が関係している記事は,以下のようなものです。
区間縮小法の原理の証明には,二つ目の記事を用いました。二つ目の記事の証明には,一つ目のデデキント切断の記事で解説している,実数の部分集合における上限(sup)・下限(inf)の存在定理を用いています。つまり,本サイトでは,区間縮小法の原理の証明に,上限(sup)・下限(inf)の存在定理を用いたわけです。
なお,区間縮小法の原理(+アルキメデス性)は,実数の連続性と同値であることが知られています。逆に,区間縮小法の原理を認めて,上限(sup)・下限(inf)の存在定理を証明することができるということです。証明してみましょう。
区間縮小法の原理から実数の連続性の証明
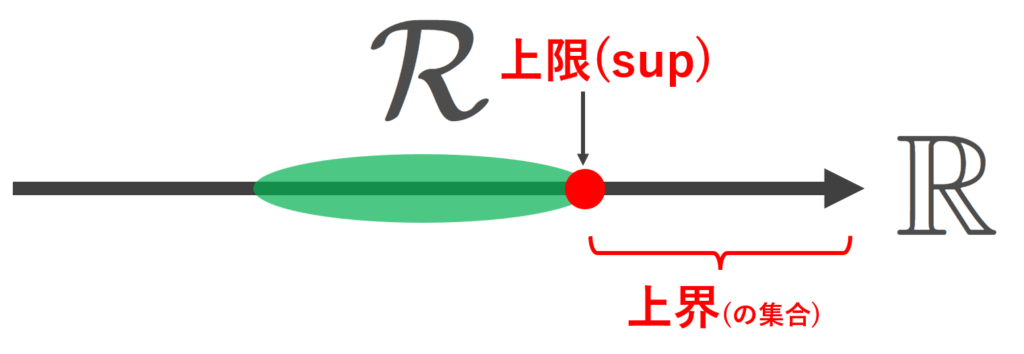
定理2(実数の連続性; \sup,\inf の存在)
\mathcal{R}\subset \mathbb{R} は空でなく,上に有界であるとする。すなわち,ある M\in \mathbb{R} が存在して,
r\le M \quad (\forall r\in \mathcal{R})
が成立すると仮定する(このような M を上界 (upper bound) という)。
このとき,\mathcal{R} の最小上界(上限 (supremum) という) M_0\in\R が存在する(この M_0 を \large\color{red}\sup \mathcal{R} とかく)。すなわち M_0 は上界であるが, M'<M_0 をみたす任意の M'\in\R は上界でないような M_0 が存在する。
同様に最小下界(下限)も考えることができる。
本定理は,デデキント切断による実数の構成を解説においては,デデキント切断を用いて証明しています。今回は区間縮小法の原理を用いて,証明してみます。
証明
b_1\in\R を上界(upper bound; UBと略すことにする)のうちの一つとし, a_1 を上界でないとする。 I_1= [a_1, b_1] とする。ここで, I_n= [a_n, b_n] とするとき,
I_{n+1} = \begin{dcases} \left[ a_n, \frac{a_n+b_n}{2}\right] &\text{ if }\tfrac{a_n+b_n}{2} \text{ is UB,}\\ \left[\frac{a_n+b_n}{2}, b_n\right] &\text{ if }\tfrac{a_n+b_n}{2} \text{ is not UB} \end{dcases}
とすることで,帰納的に閉区間の列 \{I_n\} を定める。明らかに I_1\supset I_2\supset I_3\supset \cdots であり,
であるから,区間縮小法の原理より, \bigcap_{n=1}^\infty I_n = \{c\} となる c\in\R が存在する。 c=\sup \mathcal{R} を示そう。
c が上界でないとすると, c<r となる r\in\mathcal{R} が存在する。 \bigcap_{n=1}^\infty I_n = \{c\} より,ある N\ge 1 で c\in I_N ,\, r\not\in I_N となるが,これは a_N\le c\le b_N< r を意味し, b_N が上界であることに矛盾する。よって, c は上界である。
c が最小上界(上限)でないとすると, d<c となる上界 d\in\R が存在する。 \bigcap_{n=1}^\infty I_n = \{c\} より,ある N\ge 1 で d\not\in I_N ,\, c\in I_N となるが,これは d<a_N\le c\le b_N を意味し, a_N が上界でないことに矛盾する。よって, c は最小上界(上限)である。
証明終