有理数で 1 ,無理数で 0 となる有名な関数「ディリクレ関数」について,その定義と重要な性質をまとめます。
ディリクレ関数の定義
定義(ディリクレ関数)
\color{red}1_\mathbb{Q} (x) = \begin{cases} 1 & x \in \mathbb{Q}, \\ 0 & x\in \mathbb{R} \setminus \mathbb{Q}\end{cases}
となる関数をディリクレ関数 (Dirichlet function) という。
\mathbb{Q} は有理数全体の集合, \mathbb{R} \setminus \mathbb{Q} は無理数全体の集合を指しますから,この関数は有理数上で 1 ,無理数上で 0 となる関数なわけです。
1_\mathbb{Q} というのは,定義関数(指示関数,特性関数)を用いた表記です。本記事では,この表記を用いましょう。
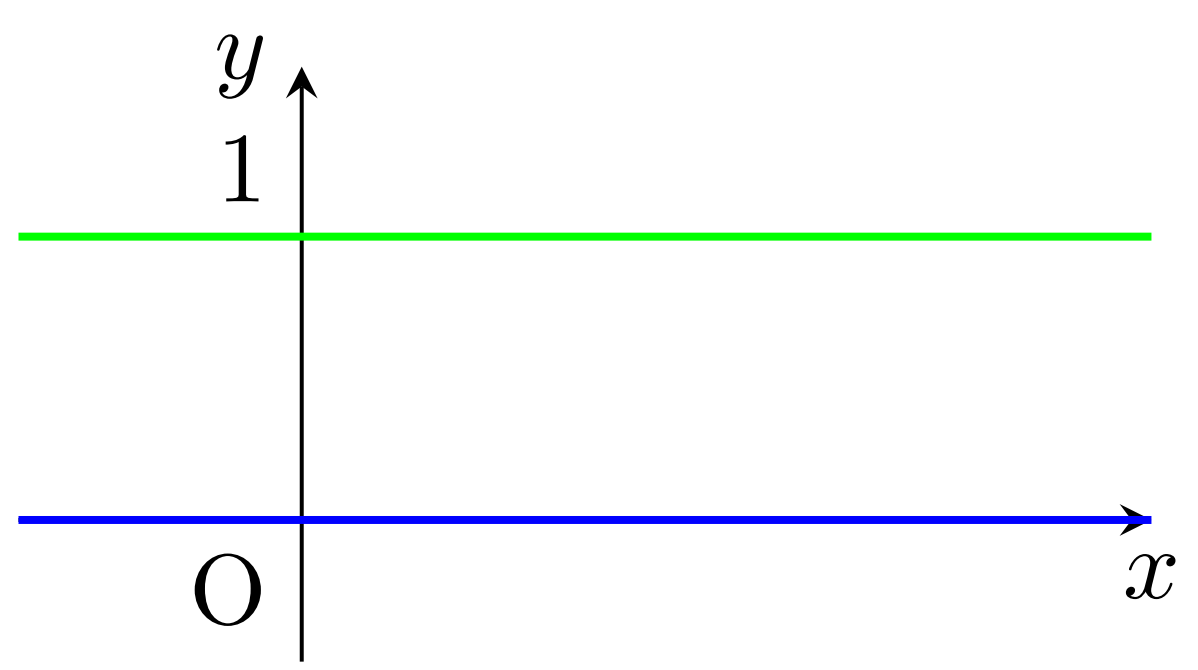
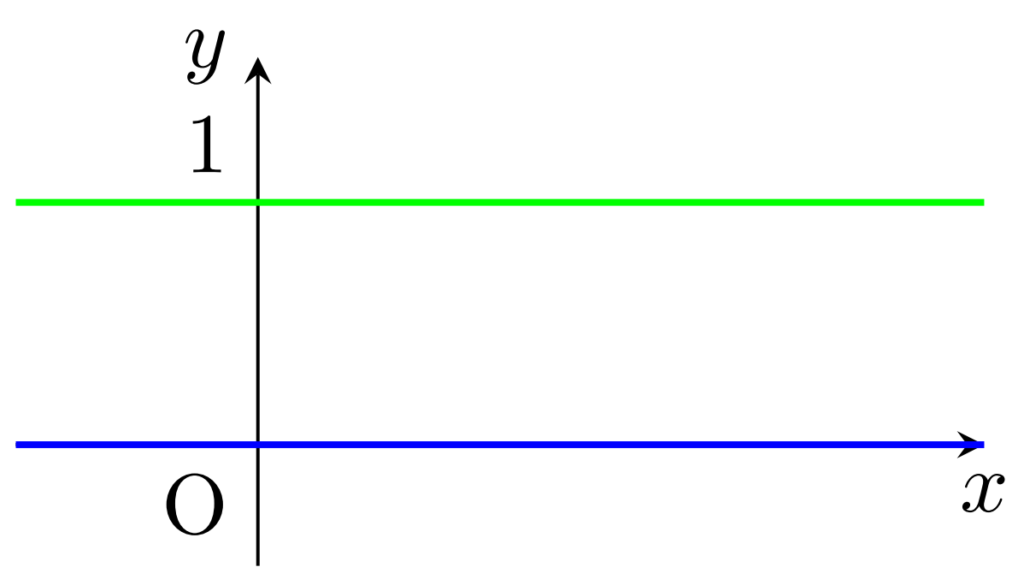
有理数・無理数は,どちらも実数上稠密(ちゅうみつ)に分布しています。すなわち,「ある区間には有理数がありません」とか,そういう状態はないわけです。従って,厳密なグラフを図示することは不可能です。
無理やりグラフを描くと,有理数では緑,無理数では青の値を取る以下のようなグラフになってしまいます(笑)。
ディリクレ関数の性質5つ
ディリクレ関数の重要な性質を5つ挙げましょう。
定理(ディリクレ関数の性質)
順番に解説していきます。
1. ディリクレ関数がいたるところ不連続であること
1. ディリクレ関数はいたるところ不連続である。
これを証明してみましょう。
証明
a \in \mathbb{R} とする。q_n \xrightarrow{n\to\infty} a となる有理数列 \{q_n\} \subset \mathbb{Q} と, r_n \xrightarrow{n\to\infty} a となる無理数列 \{r_n\} \subset \mathbb{R} \setminus \mathbb{Q} を取ってこよう。(これは有理数・無理数の稠密性より可能である。)
1_{\mathbb{Q}} (q_n) =1, \; 1_{\mathbb{Q}}(r_n)=0 であるから,
\lim_{n\to\infty} 1_{\mathbb{Q}} (q_n) = 1 \ne 0 = \lim_{n\to\infty} 1_{\mathbb{Q}} (r_n)
となって,特に \lim_{x\to a} 1_{\mathbb{Q}} (x) は存在しない。よって不連続である。
証明終
「有理数から a に近づける」のと,「無理数から a に近づける」のとで,値が変わるということは,「任意の近づけ方」をすると,値が定まらず,極限が存在しないということですね。
2. ディリクレ関数がリーマン積分不可能であること
2. ディリクレ関数は [a,b] 上リーマン積分不可能である。
リーマン積分とは,高校生や大学1-2年生が扱う積分のことです。ディリクレ関数は,リーマン積分不可能な関数として,有名な例の1つです。これを証明してみましょう。
証明
適当に a = x_0 < x_1 < x_2 < \dots < x_n = b とすることで,区間を分割し,その各区間の幅を \varDelta_k = x_k - x_{k-1} とし, t_k \in [x_{k-1}, x_k] とする。このときのリーマン和
\sum_{k=1}^n 1_{\mathbb{Q}}(t_k) \varDelta_k
について,常に t_k \in \mathbb{Q} となるように選ぶと,この値は b-a となり,常に t_k \in \mathbb{R} \setminus \mathbb{Q} となるように選ぶと, 0 となる。
これは分割の幅 |\varDelta| = \sup_k \varDelta_k を |\varDelta| \to 0 としても状況は変わらず,リーマン和の収束値は代表元 t_k の取り方に依存する。従って,リーマン積分不可能である。
証明終
リーマン積分が定義されるためには, |\varDelta| \to 0 としたときのリーマン和の収束値が,代表元 t_k の取り方に依存しない必要があったため,リーマン積分が定義できないわけです。
3. ディリクレ関数がルベーグ積分可能であること
3. ディリクレ関数 [a,b] 上ルベーグ積分可能である。
ルベーグ積分とは,専門数学において使われる積分です。ディリクレ関数は,リーマン積分不可能であるがルベーグ積分は可能である関数として,ルベーグ積分の有用性を述べる際によく取り上げられる関数の1つです。ルベーグ積分可能であることは,以下のように証明されます。
証明
\mu をルベーグ測度とすると,ルベーグ積分の定義により,
\begin{aligned} &\int_a^b 1_{\mathbb{Q}}(x) \, dx \\ &= 1\cdot \mu([a,b]\cap \mathbb{Q}) + 0 \cdot \mu([a,b] \setminus \mathbb{Q} ) \\ &= 1\cdot 0 + 0 \cdot (b-a) \\ &= 0.\end{aligned}
よってルベーグ積分は可能で, \int_a^b 1_{\mathbb{Q}}(x) \, dx = 0 となる。
証明終
有理数のルベーグ測度は \mu(\mathbb{Q}) = 0 ですから,このようなことになるわけです。
4. ディリクレ関数は連続関数の各点収束極限として表せないこと
これに関しては,以下の定理が知られています。
定理(ベール; Baire)
f\colon \mathbb{R} \to \mathbb{R} が高々1階のベール関数,すなわち連続関数またはその各点収束極限として表せる関数である必要十分条件は, f の連続点が稠密であることである。
1_{\mathbb{Q}} はいたるところ不連続であることは,項目1で述べましたね。連続点は存在しないわけなので,連続関数のの各点収束極限では表せないということです。
5. ディリクレ関数がcosの2重極限でかけること
\displaystyle1_{\mathbb{Q}}(x) =\lim_{n\to\infty} { \lim_{k\to\infty} \cos^{2k} (n!\pi x)} とかける。特に,連続関数の2重極限として表せるため,2階のベール関数である。
極限部分について,証明してみましょう。
証明
x \in \mathbb{Q} のとき, x = p/q \,\,(p,q\in \mathbb{Z}) と表すと, n \ge |q| とすることで, n!\pi x は \pi の倍数となる。従って,十分大きい n で \cos^{2k} (n!\pi x) =1 が成り立つため,
\lim_{n\to\infty} { \lim_{k\to\infty} \cos^{2k} (n!\pi x)} = 1
である。一方で, x \in \mathbb{R} \setminus \mathbb{Q} のとき,任意の n について, n! x は無理数であるから,任意の n について,-1< \cos (n!\pi x ) < 1 である。従って,任意の n について \lim_{k\to\infty} \cos^{2k}(n!\pi x) = 0 となる。これにより,
がわかる。以上2つの結果を踏まえると,結論が従う。
証明終
無事に証明できましたね。