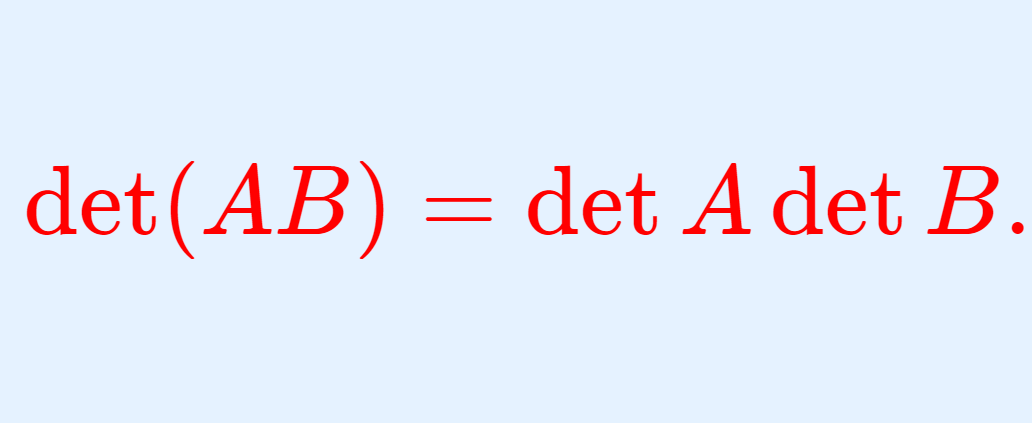行列式の性質のうち,特に大事な6つの性質を証明します。最後には,行列の基本変形と行列式の関連性についても考えます。
行列式の性質
まず最初に,今回紹介する行列式の性質を全て列挙しましょう。
以下で,複素数 \mathbb{C} は実数 \mathbb{R} に変えても成立します。
定理(行列式の性質)
1. 行列式は,各列に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元列ベクトル, s,t\in \mathbb{C} とすると,
\small \begin{aligned} &\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{s\boldsymbol{a_k}+t\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ ={}&\textcolor{red}{s} \det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{a_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ &+ \textcolor{red}{t}\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}). \end{aligned}
また同様に,行列式は各行に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元行ベクトル, s,t\in \mathbb{C} とすると,
2. 転置行列の行列式は元のそれと同じ。すなわち, \color{red}\det A = \det A^\top.
3. (列・行の入れ替え) \sigma\in S_n を置換とする。このとき,太字を列ベクトルとすると,
\begin{aligned}& \det(\boldsymbol{a_{\textcolor{red}{\sigma(1)}}}, \dots ,\boldsymbol{a_{\textcolor{red}{\sigma(n)}}})\\ & =\textcolor{red}{( \operatorname{sgn} \sigma )}\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}).\end{aligned}
太字を行ベクトルとすると,
特に, 2つの列(または行)を入れ替えると,行列式は \color{red} -1 倍になる。
4. 2つの列(または行)が等しい行列式の値は \color{red} 0 である。
5. 行列式と積は可換である。すなわち, A,B を n 次正方行列とするとき,
\color{red} \det (AB) = \det A \det B.
6. A が正則のとき, \color{red}\det (A^{-1}) = (\det A)^{-1} .
今回はこの6つについて,証明付きで扱いましょう。
行列式の性質の証明
行列式の性質の前に,行列式の定義を復習しておきましょう。
n 次正方行列 A =(a_{ij}) に対し,
\color{red} \det A = \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}
を行列式 (determinant) という。
行列式の定義について詳しくは,行列式(det)の定義と現実的な求め方~計算の手順~を参照してください。
なお, \sigma や S_n は置換による記号です。これは,線形代数(行列)における置換・奇置換・偶置換の最低限必要な知識を参照してください。
1. 行列式の列・行の線形性
1. 行列式は,各列に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元列ベクトル, s,t\in \mathbb{C} とすると,
\small \begin{aligned}&\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{s\boldsymbol{a_k}+t\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\={}&\textcolor{red}{s} \det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{a_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ &+ \textcolor{red}{t}\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}).\end{aligned}\small \begin{aligned} &\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{s\boldsymbol{a_k} +t\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} \\ &= \textcolor{red}{s}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{a_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} +\textcolor{red}{t}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} .\end{aligned}
また同様に,行列式は各行に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元行ベクトル, s,t\in \mathbb{C} とすると,
証明
列に関する線形性について
\boldsymbol{a_k} = \begin{pmatrix} a_{1k}\\ a_{2k}\\ \vdots \\ a_{nk} \end{pmatrix}
と定めると,積の分配法則により,
であるから,結論を得る。
行に関する線形性について
次の転置行列に関する性質2を用いて,列に関する線形性に帰着させればよい。
証明終
2. 転置行列の行列式は一致する
2. 転置行列の行列式は元のそれと同じ。すなわち, \color{red}\det A = \det A^\top.
証明
\begin{aligned} \det A &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}, \\ \det A^\top &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n}\\ \end{aligned}
である。ここで,第2式の右辺を,最初の添え字に対して昇順に並び替えると,
であることが分かる。 \operatorname{sgn} \sigma = \operatorname{sgn} \sigma^{-1} であるから,結局,
となって \det A^\top = \det A.
証明終
3. 列・行の入れ替えと行列式
3. (列・行の入れ替え) \sigma\in S_n を置換とする。このとき,太字を列ベクトルとすると,
\begin{aligned}& \det(\boldsymbol{a_{\textcolor{red}{\sigma(1)}}}, \dots ,\boldsymbol{a_{\textcolor{red}{\sigma(n)}}})\\& =\textcolor{red}{( \operatorname{sgn} \sigma )}\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}).\end{aligned}\begin{aligned}\det \begin{pmatrix}\boldsymbol{a_{\textcolor{red}{\sigma(1)}}} \\ \vdots \\ \boldsymbol{a_{\textcolor{red}{\sigma(n)}}} \end{pmatrix}= \textcolor{red}{(\operatorname{sgn} \sigma)} \det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_n}\end{pmatrix} .\end{aligned}
太字を行ベクトルとすると,
特に, 2つの列(または行)を入れ替えると,行列式は \color{red} -1 倍になる。
証明
行に関する置換は,転置すること(性質2)で列に関する置換に帰着されるから,列の方のみ示そう。
\boldsymbol{a_k} = \begin{pmatrix} a_{1k}\\ a_{2k}\\ \vdots \\ a_{nk} \end{pmatrix}
と定めると,
より結論を得る。
証明終
4. 2つの列(または行)が等しい行列の行列式は0
4. 2つの列(または行)が等しい行列式の値は \color{red} 0 である。
これは性質3を使って証明されます。
証明
元の行列の行列式を a とする。性質3の「2つの列(または行)を入れ替えると,行列式は -1 倍になる」という性質から,等しい2列(または2行)を入れ替えても行列式は -1 になるはずである。従って,
a = -a
より, a=0 を得る。
証明終
5. 行列式と積は可換(det AB = det A det B)
5. 行列式と積は可換である。すなわち,\color{red} \det (AB) = \det A \det B.
証明
列ベクトルを用いて, A = (\boldsymbol{a_1},\dots, \boldsymbol{a_n} ) = (a_{ij}), \,B= (b_{ij}) とすると,
\begin{aligned} AB &= \left(\sum_{i_1=1}^n \boldsymbol{a_{i_1}}b_{i_1 1}, \dots, \sum_{i_n=1}^n \boldsymbol{a_{i_n}}b_{i_n n}\right) \end{aligned}
である。これと,性質1の線形性により,
ここで,同じ列が2列以上ある行列式の値は 0 である(性質4)から,
ただし,2つ目の等式は列の置換の性質3を,最後の等式は転置行列の行列式の性質2を用いた。
証明終
6. det (A^{-1}) = (det A)^{-1}
6. A が正則のとき,\color{red} \det (A^{-1}) = (\det A)^{-1} .
証明
性質5より, I を同じ大きさの単位行列とすると,
1 = \det I = \det (AA^{-1}) = \det A \det (A^{-1}) .
従って, \det (A^{-1}) = (\det A)^{-1} .
証明終
行列の基本変形による行列式の変化
上のことを踏まえて,行列の基本変形とそれによる行列式の変化について考えましょう。行列の基本変形によって,行列式は以下のように変化します。
| 基本変形 | 行列式 | 証明方法 |
|---|---|---|
| ある行(列)の {c} 倍を他の行(列)に加える | 変化なし | 行列式の線形性(性質1) と同じ列を持つ行列式は 0 (性質4)から |
| 2つの行(列)を入れ替える | \boldsymbol{-1} 倍 | 列・行の置換の性質(性質3)から |
| ある行(列)を { c \ne 0 } 倍する | \boldsymbol{ c} 倍 | 行列式の定義から明らか |
特殊で有用な行列式
最後に,覚えておくべき特殊で有用な行列式について紹介しましょう。
ファンデルモンドの行列式
定理(ファンデルモンドの行列式)
\color{red} \begin{vmatrix} 1 & x_1 & x_1^2 & \dots &x_1^{n-1} \\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^{n-1} \end{vmatrix} = \prod_{i<j} (x_j - x_i)
が成立する。
これについての証明は,以下の記事を参照してください。
巡回行列式
定理(巡回行列式)
\color{red} \begin{aligned} &\begin{vmatrix} x_0 & x_1 & x_2 &\dots & x_{n-1} \\ x_{n-1} & x_0 & x_1 & \dots & x_{n-2} \\ x_{n-2} & x_{n-1} & x_0 & \dots & x_{n-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_1 & x_2 & x_3 & \dots & x_0 \end{vmatrix} \\ &= \prod_{\zeta} (x_0 + \zeta x_1 + \zeta^2 x_2 + \dots \zeta^{n-1} x_{n-1} ) \end{aligned}
である。ただし, \zeta は 1 の n 乗根全体にわたる。
これの証明は,以下の記事を参照してください。