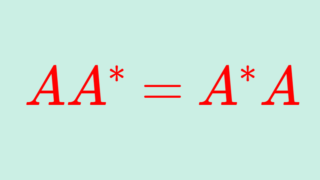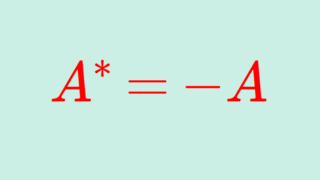エルミート行列とは,随伴行列(共役転置)と元の行列が等しい正方行列を指します。これについて,定義・具体例と性質を証明付きで紹介しましょう。
エルミート行列の定義
定義(エルミート行列)
正方行列 A が
\Large \color{red} A^* = A
をみたすとき,A をエルミート行列 (Hermitian matrix) という。ただし,A^* = \overline{A}^\top は随伴行列(複素共役)を指す。
定義は \color{red}\overline{A} =A^\top としても同じです。
エルミート行列とユニタリ行列は名前が混乱することがあるかもしれません。ユニタリ行列とは UU^*=U^*U=I_n をみたす行列です(→ユニタリ行列の定義と性質10個とその証明)。
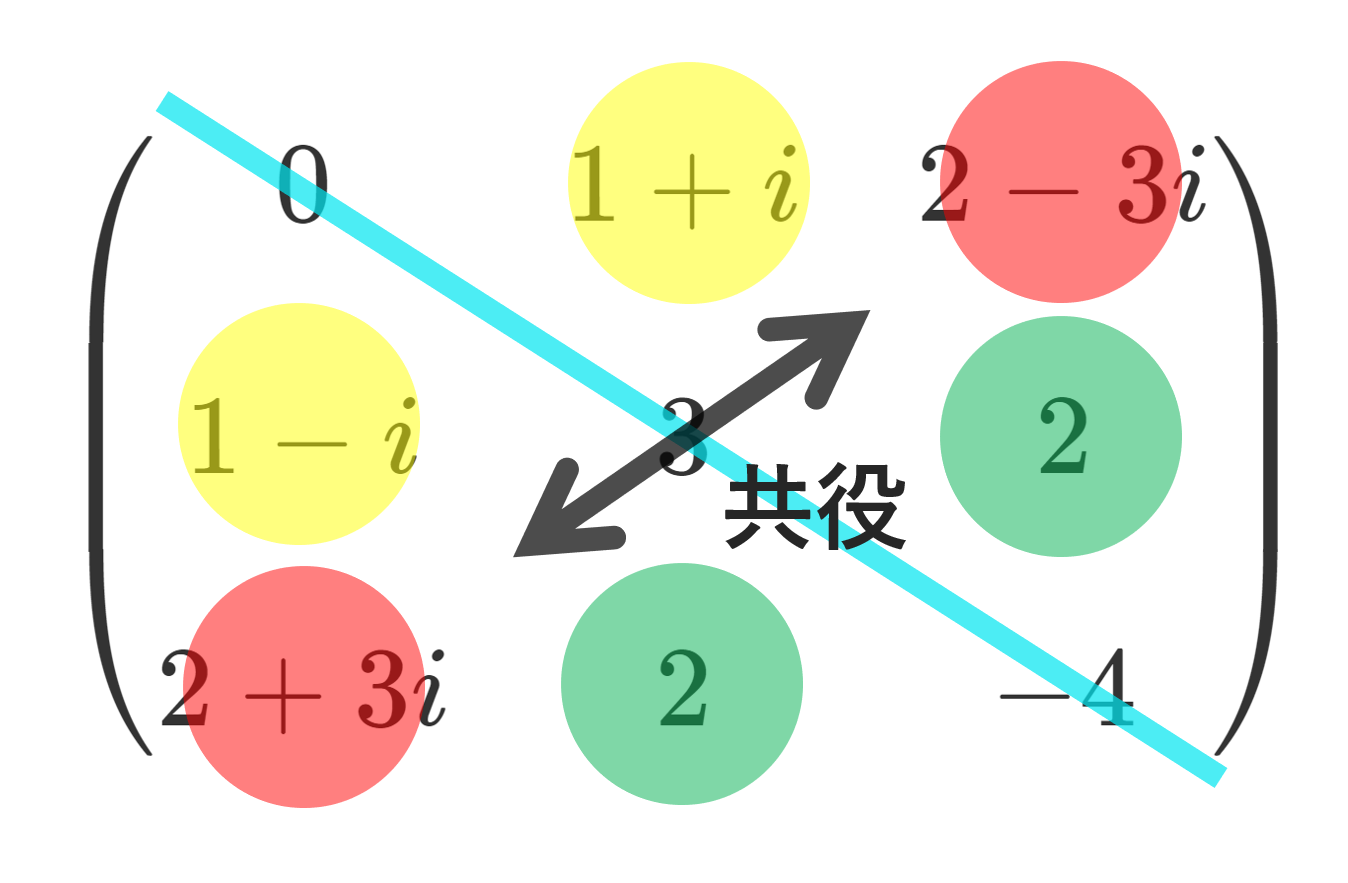
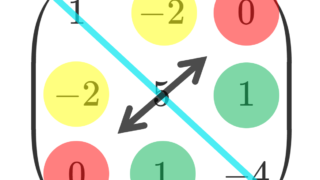
エルミート行列の具体例
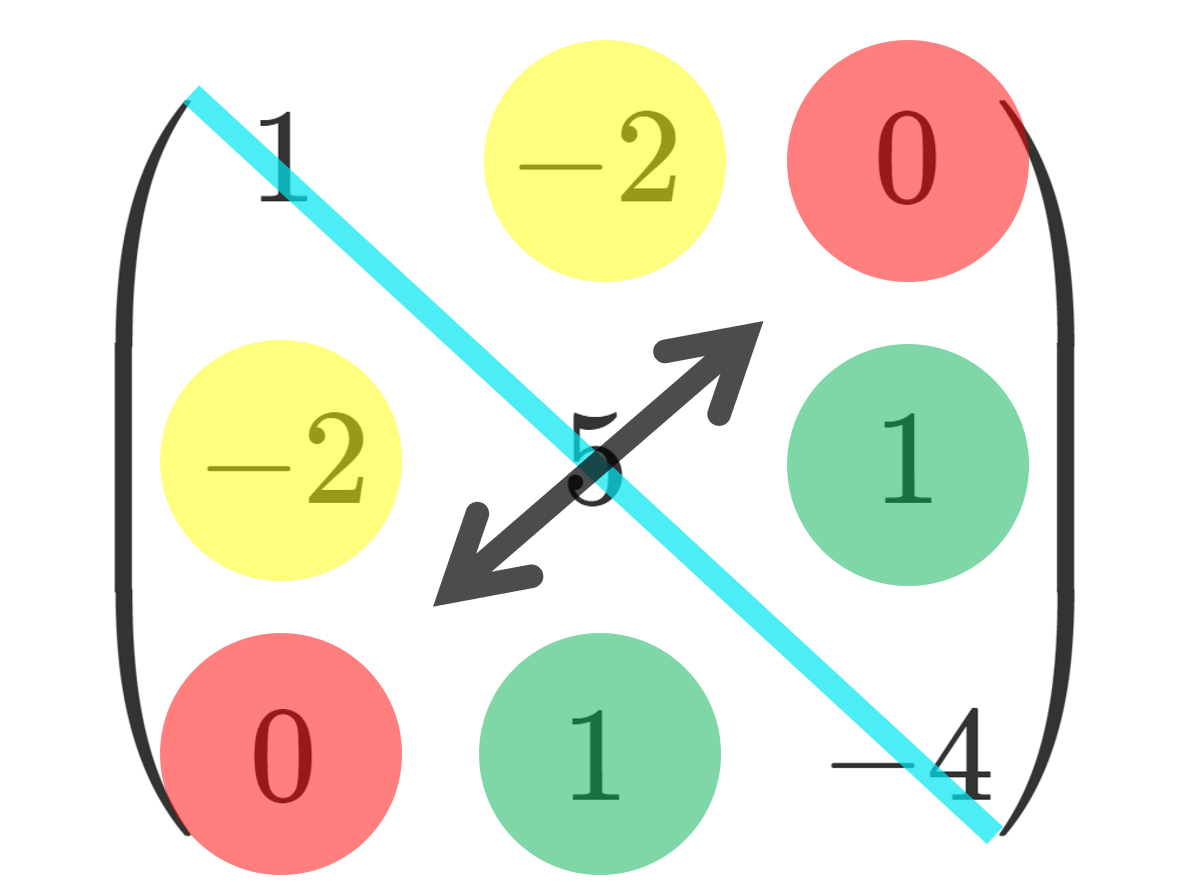
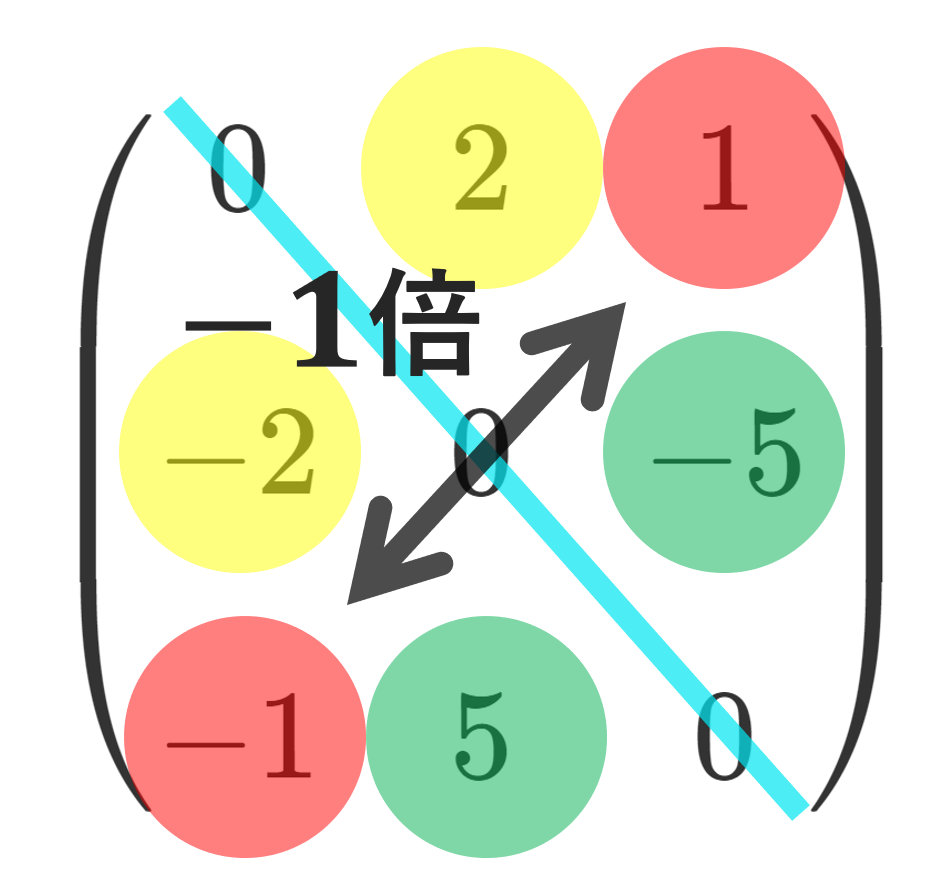
具体例を挙げましょう。
エルミート行列の具体例
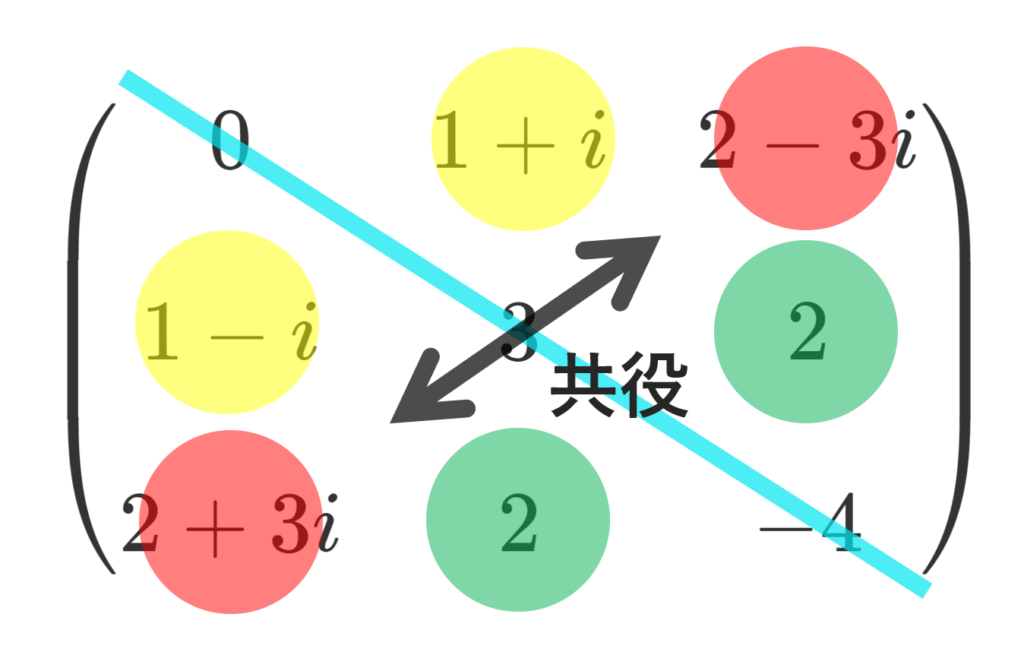
エルミート行列の対角成分は必ず実数になります。
エルミート行列の性質4つ
定理(エルミート行列の性質)
なお,エルミート行列は AA^* = A^*A が成立しますから,正規行列です。よって,正規行列がみたす性質はすべて成立します。たとえば,ユニタリ行列を用いて対角化可能です。これについては,以下で解説しています。
1. A+A^*, AA^* がエルミート行列になること
証明
\begin{aligned}&(A+A^*)^* = A^*+ (A^*)^* \\&= A^*+A=A+A^* \end{aligned}
より, A+A^* はエルミート行列ある。また,積と随伴行列(共役転置)の性質より,
より, AA^* はエルミート行列である。
証明終
任意の正方行列 A に対して,
A=\frac{1}{2}(A+A^*)+\frac{1}{2}(A-A^*)
であり, (A+A^*)/2, (A-A^*)/2 はそれぞれエルミート行列・歪エルミート行列ですから,任意の行列はエルミート行列と歪エルミート行列の和に分解できることになります。
2. <Ax,y>=<x,AY>であること
証明
内積について一般に, \langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^*\boldsymbol{y}\rangle である(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。 A^*=A であるから,題意は示された。
証明終
3. エルミート行列の行列式は実数であること
証明
\det A^* =\overline{\det A} である(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。 A^*=A より, \overline{\det A}=\det A. これは \det A が実数であることを意味する。
証明終
4. エルミート行列の固有値は実数であること
証明
\lambda\in\mathbb{C} を固有値, \boldsymbol{x} をそれに対応する固有ベクトルとすると, A\boldsymbol{x}=\lambda \boldsymbol{x} である。性質2.より, \langle A\boldsymbol{x},\boldsymbol{x}\rangle = \langle \boldsymbol{x},A\boldsymbol{x}\rangle であるので,
\lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle = \overline{\lambda} \langle\boldsymbol{x},\boldsymbol{x}\rangle .
すなわち (\lambda -\overline{\lambda})\lVert \boldsymbol{x}\rVert^2=0 であり, \lambda =\overline{\lambda}. これは \lambda が実数であることを意味する。
証明終
途中で用いたのは内積の共線形性ですね。 \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle = \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle ,\; \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle =\overline{ \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{ \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle です。