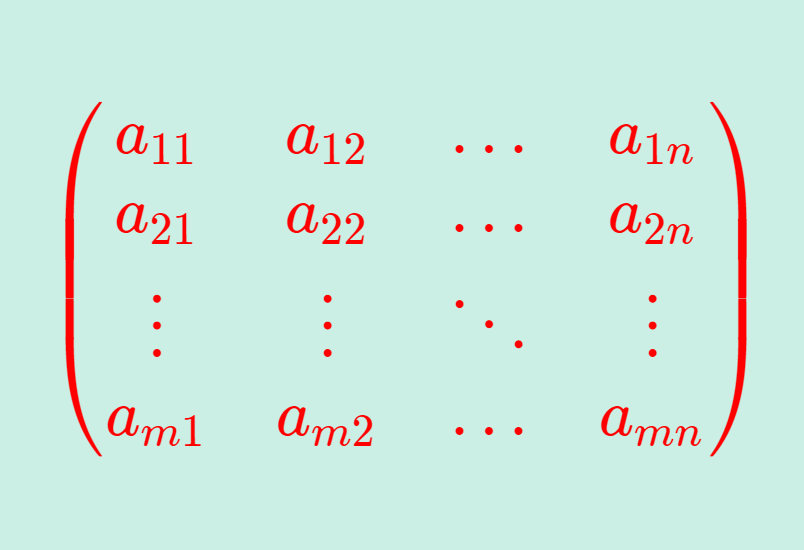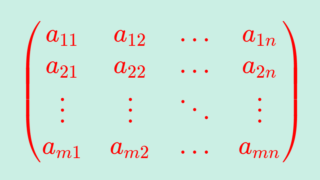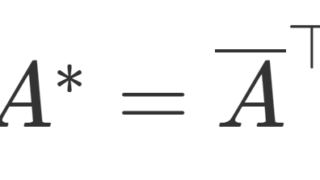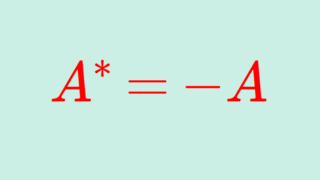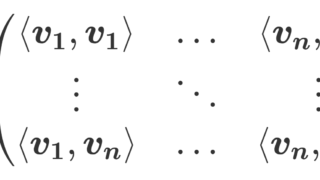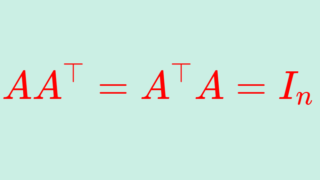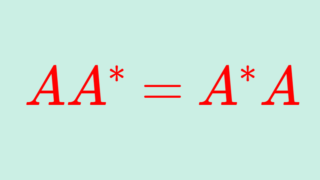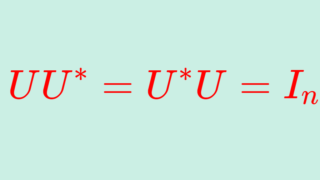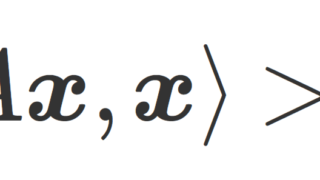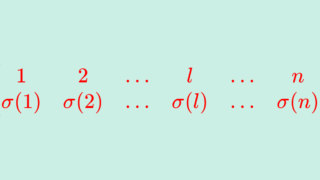名前の付いた,さまざまな行列をまとめます。本サイト内で解説のあるものは,そのリンクを一緒に載せます。
基本的な行列
以下の4つは,次の記事で解説しています。
m×n行列
A=\begin{pmatrix} a_{11}& a_{12}&\dots &a_{1n}\\ a_{21}&a_{22}&\dots & a_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ a_{m1}&a_{m2} &\dots & a_{mn}\end{pmatrix}
正方行列
A=\begin{pmatrix} a_{11}& a_{12}&\dots &a_{1n}\\ a_{21}&a_{22}&\dots & a_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ a_{n1}&a_{n2} &\dots & a_{nn}\end{pmatrix}
零行列
O=\begin{pmatrix} 0& 0&\dots &0\\ 0&0&\dots & 0 \\ \vdots &\vdots & \ddots & \vdots\\ 0&0&\dots & 0\end{pmatrix}
単位行列
I=\begin{pmatrix} 1& 0&\dots &0\\ 0&1&\dots & 0 \\ \vdots &\vdots & \ddots & \vdots\\ 0&0 &\dots & 1\end{pmatrix}
ゼロの場所で区別
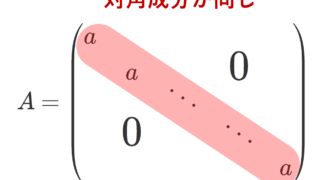
スカラー行列
S=\begin{pmatrix} a& &&\huge{0}\\ &a& & \\ && \ddots& \\ \huge{0}& && a\end{pmatrix}
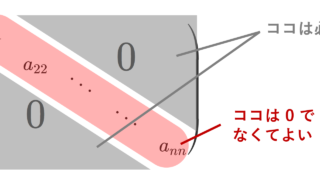
対角行列
D=\begin{pmatrix} a_{11}& &&\huge{0}\\ &a_{22}& & \\ && \ddots& \\ \huge{0}& && a_{nn}\end{pmatrix}
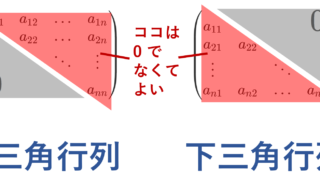
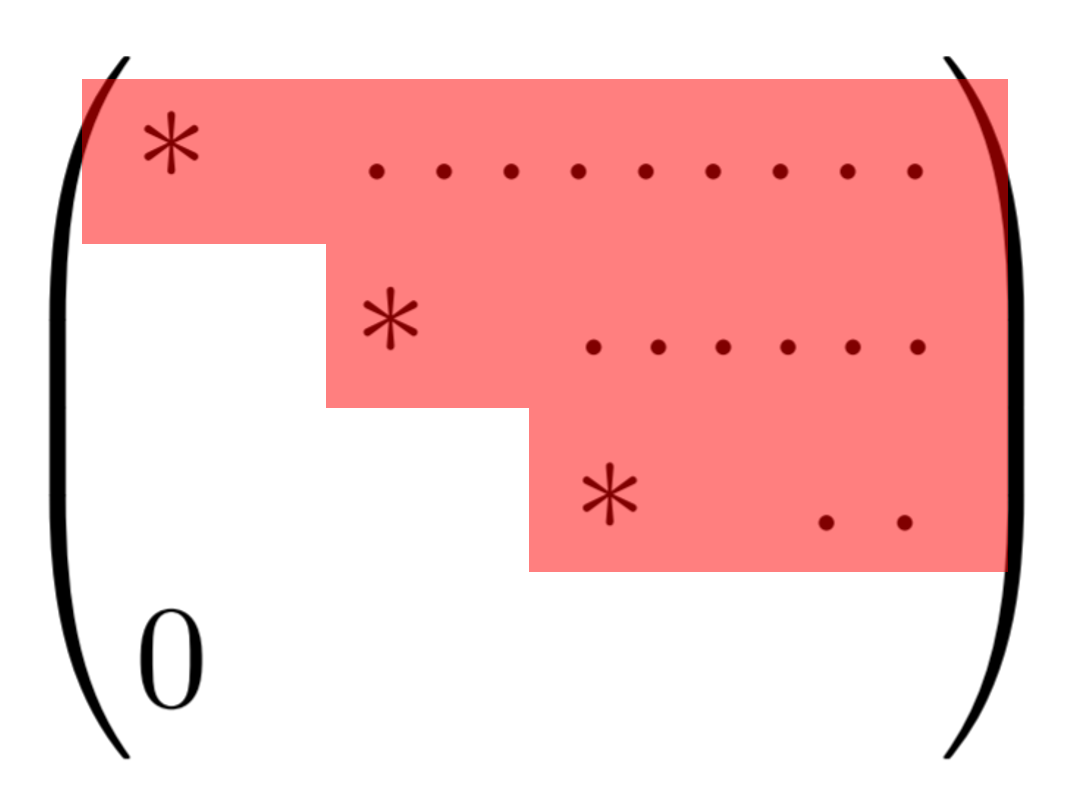
三角行列(上三角・下三角)
\begin{aligned}A&=\begin{pmatrix} a_{11}& &&\huge{*}\\ &a_{22}& & \\ && \ddots& \\ \huge{0}& && a_{nn}\end{pmatrix},\\ B&=\begin{pmatrix} a_{11}& &&\huge{0}\\ &a_{22}& & \\ && \ddots& \\ \huge{*}& && a_{nn}\end{pmatrix} \end{aligned}
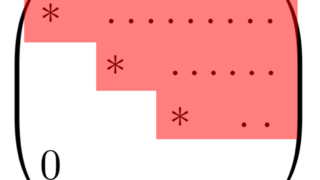
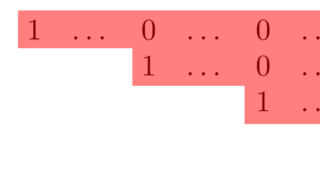
階段行列
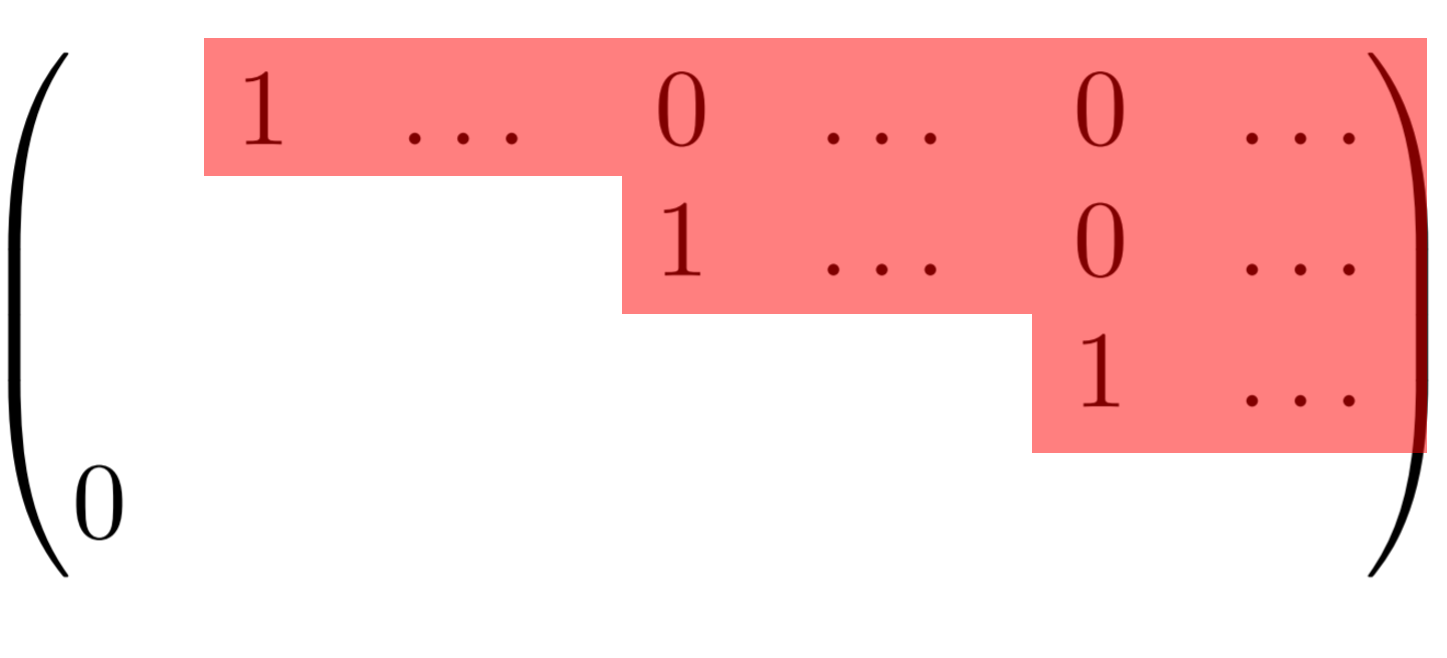
RREF行列
三重対角行列
\begin{pmatrix} a_{11}& a_{12}&&&\huge{0}\\ a_{21}&a_{22}&a_{23} & \\ & a_{32} & a_{33} & \ddots \\ &&\ddots &\ddots& \ddots \\ &&&\ddots &\ddots&a_{n-1\, n}\\ \huge{0}& &&&a_{n\,n-1}& a_{nn}\end{pmatrix}
成分入れ替えによる区別
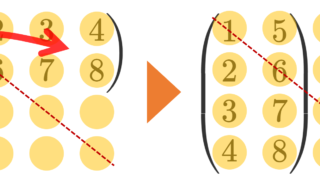
転置行列
A^\top=\begin{pmatrix} a_{11}& a_{21}&\dots &a_{m1}\\ a_{12}&a_{22}&\dots & a_{m2} \\ \vdots &\vdots & \ddots & \vdots\\ a_{1n}&a_{2n} &\dots & a_{mn}\end{pmatrix}
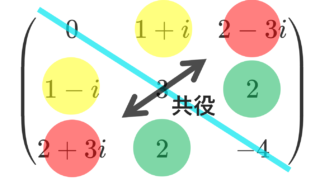
随伴行列
A^*=\overline{A}^\top=\begin{pmatrix} \overline{a}_{11}& \overline{a}_{21}&\dots &\overline{a}_{m1}\\ \overline{a}_{12}&\overline{a}_{22}&\dots & \overline{a}_{m2} \\ \vdots &\vdots & \ddots & \vdots\\ \overline{a}_{1n}&\overline{a}_{2n} &\dots & \overline{a}_{mn}\end{pmatrix}
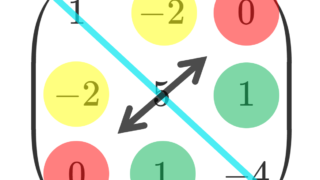
対称行列
A^\top=A
エルミート行列
A^*=A
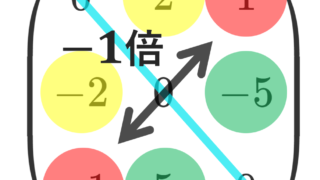
交代行列(反対称行列・歪対称行列)
A^\top = -A
歪エルミート行列(反エルミート行列)
A^*= -A
巡回行列
\begin{pmatrix} x_0&x_1&x_2&\dots & x_{n-1}\\ x_{n-1}& x_0 & x_1 & \dots & x_{n-2}\\ x_{n-2} & x_{n-1}& x_0 &\dots & x_{n-3}\\ \vdots & \vdots& \vdots & \ddots & \vdots\\ x_1 & x_2& x_3 & \dots & x_0\end{pmatrix}
ファンデルモンド行列
\begin{pmatrix} 1&x_1&x_1^2&\dots & x_1^{n-1}\\ 1& x_2 & x_2^2 & \dots & x_2^{n-1}\\ \vdots & \vdots& \vdots & \ddots & \vdots\\ 1& x_n& x_n^2 & \dots & x_n^{n-1}\end{pmatrix}
テプリッツ行列
\begin{pmatrix}a_0 &a_{-1}& a_{-2} &\dots & \dots &a_{-n+1} \\ a_1&a_0 &a_{-1} &\ddots & \ddots & \vdots \\ a_2 & a_1 & \ddots &\ddots & \ddots & \vdots \\ \vdots& \ddots & \ddots &\ddots & a_{-1} & a_{-2}\\ \vdots & \ddots & \ddots & a_1 & a_0 & a_{-1} \\ a_{n-1}&\dots & \dots & a_2&a_1&a_0\end{pmatrix}
ハンケル行列
\begin{pmatrix}a_0&a_1 & a_2 & \dots &a_{n-1}&a_n \\ a_1 & a_2 & \ddots & \ddots & a_n & a_{n+1} \\ a_2 & \ddots & \ddots & \ddots& \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & a_{2n-2}\\ a_{n-1}& a_n & \ddots &\ddots & a_{2n-2}& a_{2n-1}\\ a_n & a_{n+1} & \dots & a_{2n-2} & a_{2n-1} & a_{2n} \end{pmatrix}
積による演算で区別
逆行列・正則行列
AA^{-1} = A^{-1}A=I
グラム行列
G=A^* A
直交行列
AA^\top=A^\top A=I
正規行列
AA^* = A^*A
ユニタリ行列
UU^*=U^*U=I
正定値行列・半正定値行列
A は実対称行列で,任意の \boldsymbol{x}\in \mathbb{R}^n\setminus \{\boldsymbol{0}\} に対して,
\boldsymbol{x}^\top A\boldsymbol{x}>0\quad (\ge 0)
射影行列
P^2=P,\quad P^*=P
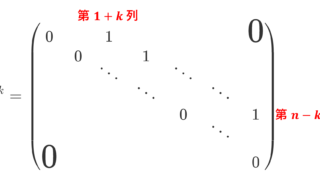
べき零行列
A^k =O
ベクトル空間と強く関連した行列
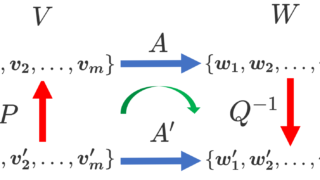
表現行列
(f(\boldsymbol{v_1}),\dots, f(\boldsymbol{v_m}))= (\boldsymbol{w_1},\dots, \boldsymbol{w_n}) A
基底の変換行列
(\boldsymbol{v'_1},\dots, \boldsymbol{v'_n})= (\boldsymbol{v_1},\dots, \boldsymbol{v_n}) P
線形代数におけるその他の重要な行列
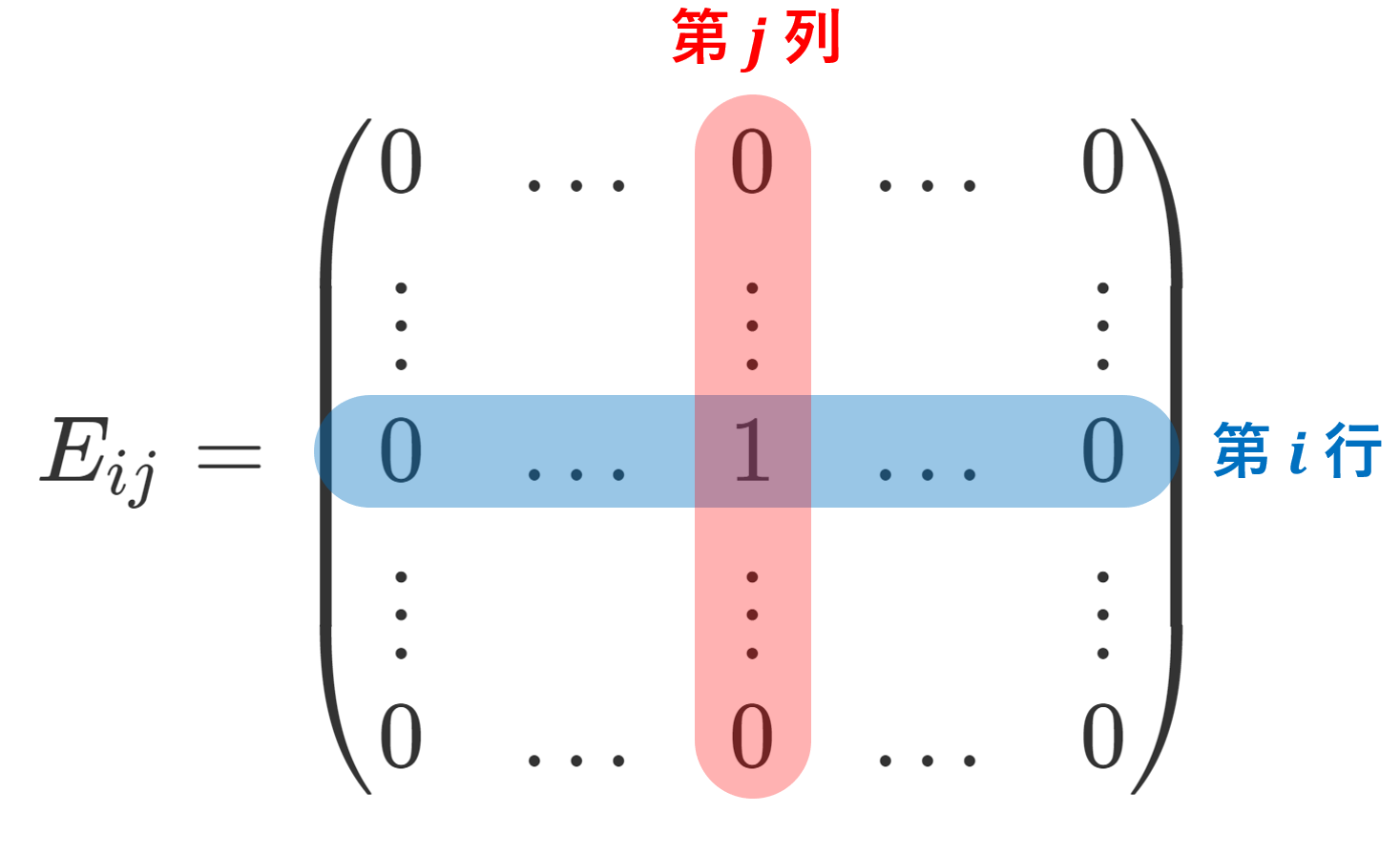
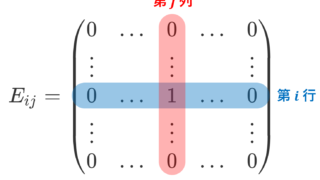
行列単位
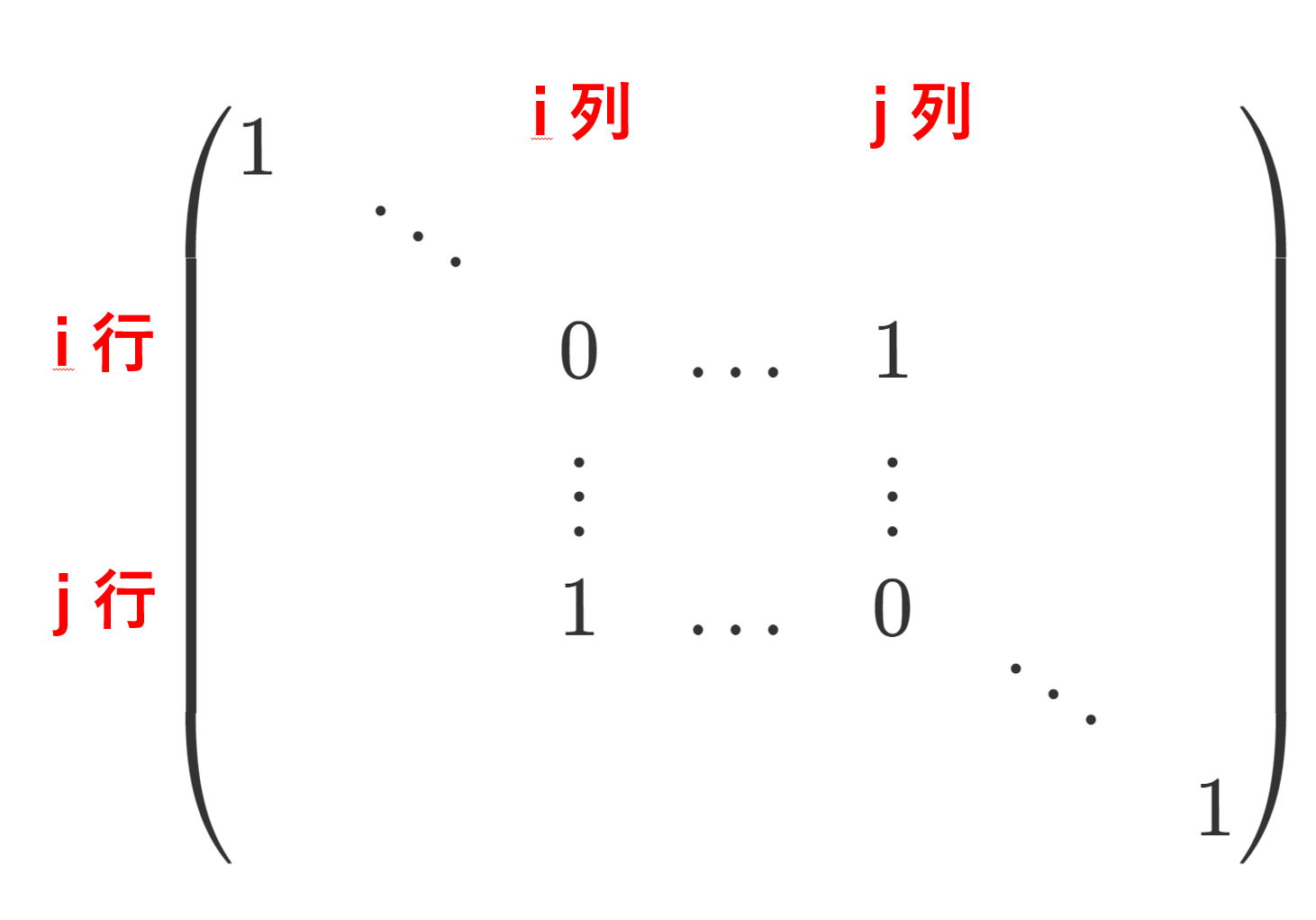
基本行列
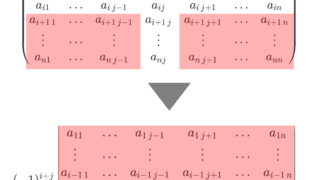
余因子行列
\tilde{A}=\begin{pmatrix} \tilde{a}_{11}& \tilde{a}_{12}&\dots &\tilde{a}_{1n}\\ \tilde{a}_{21}&\tilde{a}_{22}&\dots & \tilde{a}_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ \tilde{a}_{m1}&\tilde{a}_{m2} &\dots & \tilde{a}_{mn}\end{pmatrix}ただし,
\scriptsize\!\!\!\!\!\!\!\!\tilde{a}_{ij}=(-1)^{i+j}\begin{vmatrix}a_{11}&\dots &a_{1\,j-1}&a_{1\,j+1}&\dots & a_{1n}\\ \vdots& \cdots &\vdots & \vdots& \cdots & \vdots \\ a_{i+1\,1}&\dots & a_{i+1\,j-1}&a_{i+1\,j+1}&\dots & a_{i+1\,n} \\ \vdots& \cdots &\vdots & \vdots& \cdots & \vdots \\ a_{n1} &\dots & a_{n\,j-1}&a_{n\,j+1}&\dots&a_{nn} \end{vmatrix}
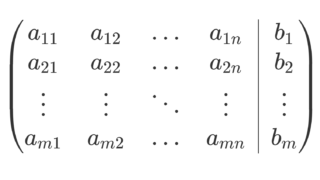
係数行列・拡大係数行列
連立一次方程式
\begin{cases} a_{11}x_1+a_{12}x_2+\dots +a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\ \cdots\\ a_{m1}x_1+a_{m2}x_2+\dots+a_{mn}x_n =b_m\end{cases}\begin{aligned}&\begin{pmatrix} a_{11}& a_{12}&\dots &a_{1n}\\ a_{21}&a_{22}&\dots & a_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ a_{m1}&a_{m2} &\dots & a_{mn}\end{pmatrix}, \\ &\begin{pmatrix} a_{11}& a_{12}&\dots &a_{1n}&b_1\\ a_{21}&a_{22}&\dots & a_{2n} &b_2\\ \vdots &\vdots & \ddots & \vdots&\vdots\\ a_{m1}&a_{m2} &\dots & a_{mn}&b_m\end{pmatrix}\end{aligned}
に対して,
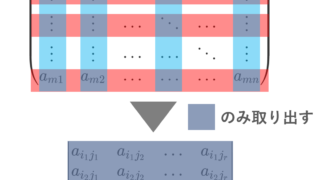
小行列
\begin{pmatrix} a_{i_1i_1}& a_{i_1i_2}&\dots &a_{i_1i_s}\\ a_{i_2i_1}&a_{i_2i_2}&\dots & a_{i_2i_s} \\ \vdots &\vdots & \ddots & \vdots\\ a_{i_ri_1}&a_{i_ri_2} &\dots & a_{i_ri_s}\end{pmatrix}
ブロック行列(区分行列)
A= \begin{pmatrix}A_{11} & A_{12} & \dots & A_{1n}\\ A_{21} & A_{22} & \dots & A_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{m1} & A_{m2} & \dots & A_{mn} \end{pmatrix}
ただし, A_{ij} は適切な形の行列(小行列)
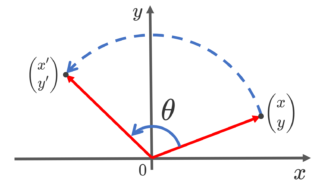
回転行列
R_\theta = \begin{pmatrix} \cos\theta& -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}
置換行列
\begin{pmatrix}1&2& \dots & n \\ \sigma(1)&\sigma(2)&\dots & \sigma(n) \end{pmatrix}
ただし, \sigma\colon \{1,2,\dots,n\}\to \{1,2,\dots, n\} は全単射
解析学と密接に関連した行列
ヤコビ行列
Jf= \begin{pmatrix} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} &\dots &\dfrac{\partial f_1}{\partial x_n}\\ \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} &\dots &\dfrac{\partial f_2}{\partial x_n}\\ \vdots &\vdots& \ddots & \vdots \\ \dfrac{\partial f_m}{\partial x_1}& \dfrac{\partial f_m}{\partial x_2}&\dots & \dfrac{\partial f_m}{\partial x_n}\end{pmatrix}
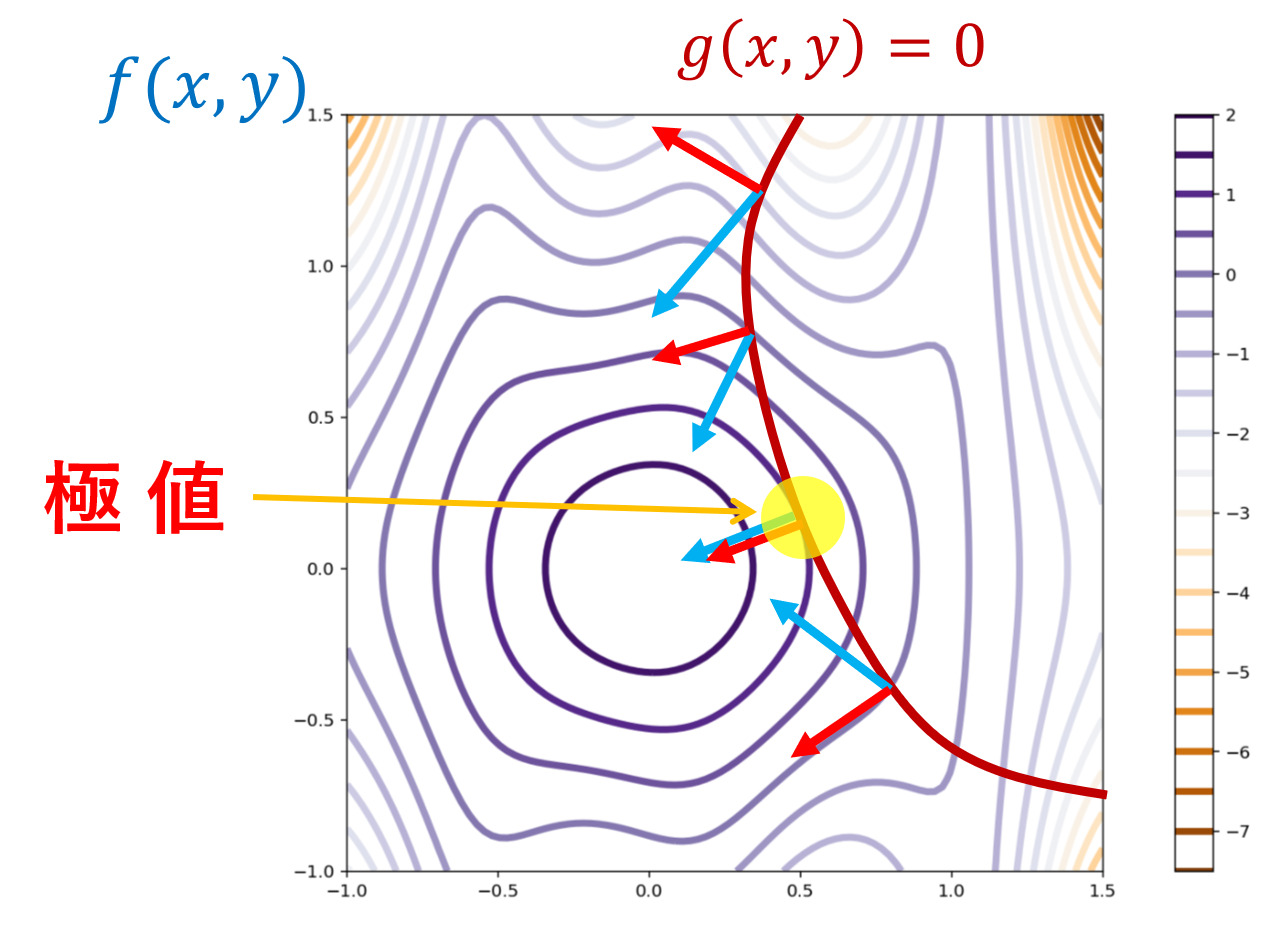
ヘッセ行列
\!\!\!\! Hf = \begin{pmatrix}\dfrac{\partial ^2 f}{\partial x_1^2}& \dfrac{\partial^2 f}{\partial x_1 \partial x_2} &\dots & \dfrac{\partial^2 f}{\partial x_1\partial x_n}\\ \dfrac{\partial ^2 f}{\partial x_2\partial x_1}& \dfrac{\partial^2 f}{\partial x_2^2 } &\dots & \dfrac{\partial^2 f}{\partial x_2\partial x_n}\\ \vdots &\vdots& \ddots & \vdots \\ \dfrac{\partial ^2 f}{\partial x_n\partial x_1}& \dfrac{\partial^2 f}{\partial x_n \partial x_2} &\dots & \dfrac{\partial^2 f}{\partial x_n^2} \end{pmatrix}
ロンスキー行列
Wf= \begin{pmatrix} f_1 & f_2 & \dots & f_n \\ f'_1 &f'_2& \dots & f'_n \\ \vdots & \vdots & \ddots & \vdots \\ f_1^{(n-1)} & f_2^{(n-1)} & \dots & f_n^{(n-1)}\end{pmatrix}
確率関係の行列
確率行列
P=\begin{pmatrix} p_{11}& p_{12}&\dots &p_{1n}\\ p_{21}&p_{22}&\dots & p_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ p_{n1}&p_{n2} &\dots & p_{nn}\end{pmatrix}
ただし,\mathbb{P}(i\to j)=p_{ij}\ge 0 ,\; \sum_{j=1}^n p_{ij}=1
分散共分散行列
\begin{pmatrix} \sigma_{11}& \sigma_{12}&\dots &\sigma_{1n}\\ \sigma_{21}&\sigma_{22}&\dots & \sigma_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ \sigma_{n1}&\sigma_{n2} &\dots & \sigma_{nn}\end{pmatrix}
ただし, \sigma_{ij} = \mathbb{E}[(X_i-\mu_i)(X_j-\mu_j)] (共分散)
相関行列
\begin{pmatrix} 1& \rho_{12}&\dots &\rho_{1n}\\ \rho_{21}&1&\dots & \rho_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ \rho_{n1}&\rho_{n2} &\dots & 1\end{pmatrix}
ただし, \rho_{ij} =\dfrac{\sigma_{ij}}{\sigma_i\sigma_j} (相関係数)
その他の行列
隣接行列
グラフ理論における有限グラフで,頂点間がつながっているかどうか,つながっているのであればその辺の重みはいくらかを表す行列
パウリ行列
\begin{aligned}\sigma_1&=\begin{pmatrix} 0&1\\1&0\end{pmatrix}, \\ \sigma_2&=\begin{pmatrix} 0&-i\\i&0\end{pmatrix},\\ \sigma_3&=\begin{pmatrix} 1&0\\0&-1\end{pmatrix}\end{aligned}
ヒルベルト行列
H=\begin{pmatrix} H_{11}& H_{12}&\dots &H_{1n}\\ H_{21}&H_{22}&\dots & H_{2n} \\ \vdots &\vdots & \ddots & \vdots\\ H_{n1}&H_{n2} &\dots & H_{nn}\end{pmatrix}
ただし,H_{ij}=\dfrac{1}{i+j-1}
アダマール行列
各成分が 1 または -1 であり,各行ベクトルが互いに直交している正方行列
まだ個別の解説が少ないですから,今後増やしていこうと思います。