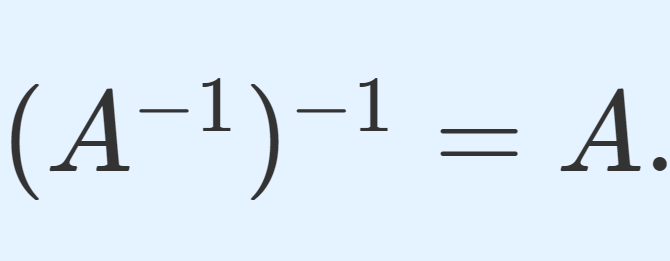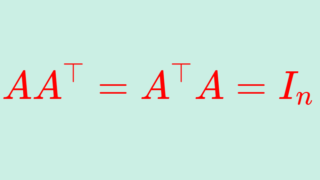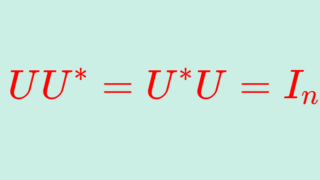正方行列が正則であるとは,逆行列が存在することを指します。これについて,その定義と性質11個を,証明付きで順に紹介しましょう。
正則行列の定義
定義(正則行列)
A が逆行列 A^{-1} をもつ,すなわち, AA^{-1} = A^{-1} A = I となる同じ形の正方行列 A^{-1} をもつとき, A は正則 (regular) であるといい,そのような行列を正則行列 (regular matrix) という。
なお,複素数を成分に持つ n 次正則行列全体の集合を \color{red} GL_n(\mathbb{C}) と表すことがある。
逆行列が存在するような行列を正則行列というのですね。
行列が正則であるとき,その逆行列の求め方(計算方法)は以下の記事で解説しています。
正則行列の性質11個
正則行列の大事な性質を挙げましょう。これが今回の本題です。
定理(正則行列の性質)
A,B を n 次正則行列とするとき,
- A に対し,逆行列 A^{-1} は一意に定まる。
- (A^{-1})^{-1} = A .
- (A^\top)^{-1} = (A^{-1})^\top . (転置行列)
- (A^*)^{-1} = (A^{-1})^* . (随伴行列(共役転置))
- (AB)^{-1} = B^{-1} A^{-1} . (行列の積)
- \det (A^{-1}) = (\det A)^{-1} . (行列式)
- \tilde{A} を A の余因子行列とすると, \tilde{A} = (\det A) A^{-1}.
- A の固有値を \lambda_1,\lambda_2,\dots, \lambda_n とすると, A^{-1} の固有値は \lambda_1^{-1},\lambda_2^{-1},\dots, \lambda_n^{-1} である。また,対応する固有ベクトルは同じである。
- 上三角行列の逆行列は上三角行列である。
- A を直交行列とすると,A^{-1}= A^\top である。
- U をユニタリ行列とすると,U^{-1} = U^* である。
一つずつ順番に証明していきましょう。
正則行列の性質11個の証明
1. 逆行列の一意性
1. A に対し,逆行列 A^{-1} は一意に定まる。
逆行列の一意性であり,最も基本的で重要な性質と言えるでしょう。証明していきます。
証明
A,B,C を n 次正方行列, I を n 次単位行列とし,
AB = BA = I, \quad AC=CA = I
が成立するとしよう。このとき,
より,B=C なので,逆行列は一意である。
証明終
2. 逆行列の逆行列
2. (A^{-1})^{-1} = A .
証明
AA^{-1} = A^{-1}A = I であるから, A は,A^{-1} の逆行列と見れる。逆行列の一意性(性質1)より,
(A^{-1})^{-1} = A.証明終
3. 逆行列の転置は転置の逆行列に等しい
3. (A^\top)^{-1} = (A^{-1})^\top . (転置行列)
証明
(AB)^\top = B^\top A^\top を用いる(→転置行列の定義と基本的な性質の証明)。 I を n 次単位行列とすると,
\begin{gathered} (A^{-1})^\top A^\top = (A A^{-1})^\top = I , \\ A^\top (A^{-1})^\top = (A^{-1} A)^\top = I \end{gathered}
となり,これは (A^\top)^{-1} =(A^{-1})^\top を意味する。
証明終
4. 逆行列の随伴行列(共役転置)は随伴行列(共役転置)の逆行列に等しい
4. (A^*)^{-1} = (A^{-1})^* . (随伴行列(共役転置))
これは,転置行列と逆行列の性質3で,各成分について共役を取ったものであるため,3を用いれば,4が成り立つことは明らかでしょう。
5. 行列の積と逆行列の関係
5. (AB)^{-1} = B^{-1} A^{-1} . (行列の積)
証明
\small\begin{gathered}(AB)(B^{-1}A^{-1}) = A(BB^{-1})A^{-1} = AA^{-1} = I, \\ (B^{-1}A^{-1})(AB)= B^{-1}(A^{-1}A)B=B^{-1}B=I\end{gathered}
である。これは,行列 AB の逆行列が B^{-1}A^{-1} であることを意味する。すなわち, (AB)^{-1}=B^{-1}A^{-1}.
証明終
6. 逆行列の行列式
6. \det (A^{-1}) = (\det A)^{-1} . (行列式)
証明
1 = \det I = \det (AA^{-1}) = \det A \det (A^{-1}) .
従って, \det (A^{-1}) = (\det A)^{-1} .
証明終
n 次正方行列 A,B に対して, \det (AB) =\det A \det B になることを用いましたが,これについては,行列式の性質6つの証明(列,行の線形性,置換,積,転置など)を参照してください。
7. 逆行列と余因子行列の関係
7. \tilde{A} を A の余因子行列とすると, \tilde{A} = (\det A )A^{-1}.
これは,以下の中で証明しています。
8. 逆行列の固有値は逆数になる
8. A の固有値を \lambda_1,\lambda_2,\dots, \lambda_n とすると, A^{-1} の固有値は \lambda_1^{-1},\lambda_2^{-1},\dots, \lambda_n^{-1} である。また,対応する固有ベクトルは同じである。
そもそも,行列が正則である \iff すべての固有値が 0 でないが成り立つことに注意しましょう(→固有値の定義と求め方をていねいに~計算の手順~)。
証明
固有値 \lambda に対応する固有ベクトルを \boldsymbol{v} とする。このとき,
A\boldsymbol{v} = \lambda\boldsymbol{v}
が成立する。両辺 A^{-1} を左からかけて
よって,
であるから, A^{-1} は固有値 \lambda^{-1} をもち,対応する固有ベクトル \boldsymbol{v} は, A の \lambda に対する固有ベクトルと同じである。
証明終
9. 上三角行列の逆行列は上三角行列である
9. 上三角行列の逆行列は上三角行列である。
これについては,上三角行列・下三角行列の定義と性質6つを参照してください。
10. 直交行列の逆行列は,転置行列に等しい
10. A を直交行列とすると,A^{-1}= A^\top である。
これは,直交行列の定義から明らかです。直交行列の定義を確認しましょう。
n 次正方行列 A が直交行列 (orthogonal matrix) であるとは,
\color{red}AA^\top = A^\top A = I
が成立することである。
本来, A^{-1} が来るべきはずところに, A^\top が来ているので,A^{-1}= A^\top なわけですね。 直交行列は以下で解説しています。
11. ユニタリ行列の逆行列は,随伴行列(共役転置)に等しい
11. U をユニタリ行列とすると,U^{-1} = U^* である。
これも,ユニタリ行列の定義から明らかです。ユニタリ行列の定義を確認しておきましょう。
n 次正方行列 A がユニタリ行列 (unitary matrix) であるとは,
\color{red}AA^* = A^* A = I
が成立することである。ただし, A^*=\overline{A}^\top (随伴行列,共役転置)である。
本来, A^{-1} が来るべきはずところに, A^* が来ているので,A^{-1}= A^* なわけですね。ユニタリ行列は以下で解説しています。