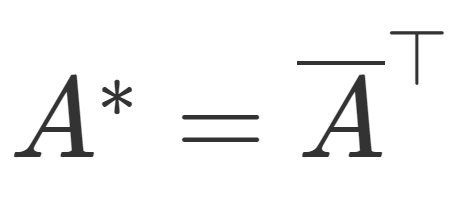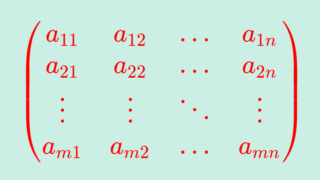随伴行列,あるいはエルミート転置や共役転置と呼ばれる行列は,元の行列の各成分で複素共役を取り,それを転置させた行列 A^*=\overline{A}^\top のことを指します。
これについて,その定義と具体例,性質を詳しく解説しましょう。
随伴行列(エルミート転置,共役転置)の定義
複素数 z = x+iy に対し,その共役複素数を,上にバーをつけて \overline{z} = x-iy とかきます。
定義(随伴行列)
A=(a_{ij}) を m\times n 行列とする。 A の各成分で複素共役を取り,転置させた n\times m 行列
\large\color{red} A^*=\overline{A}^\top=(\overline{a}_{ij})^\top = (\overline{a}_{ji})
を随伴行列 (adjoint matrix) または エルミート転置 (共役転置; Hermitian transpose) という。
随伴行列は \color{red} A^* とかくことが多い。他に, \color{red} A^\dagger とかくこともある。
共役を取って転置するのと,転置して共役を取るのはどちらも同じですから,順番を気にする必要はありません。
全ての成分が実数の行列においては,ただの転置行列と同じになります。
具体的に各成分を書き下してみましょう。
A = \begin{pmatrix}a_{11} & a_{12} & \dots & a_{1n} \\ a_{21}&a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{pmatrix}
とします。これの随伴行列は
ですね。右下の添え字は mn のままですが,n\times m 行列になっていることに注意してください。
随伴行列(エルミート転置,共役転置)の具体例
具体例を挙げておきましょう。
随伴行列の具体例
- \begin{pmatrix} 1 & i \\ 0 & 2-i \end{pmatrix}^*= \begin{pmatrix} 1 & 0 \\ -i & 2+i \end{pmatrix}
- \begin{pmatrix} 1 & 2+i & 2i\\ 1-i & -3i& 0 \end{pmatrix}^*= \begin{pmatrix} 1 & 1+i \\ 2-i & 3i \\ -2i & 0 \end{pmatrix}
他に,複素列ベクトルの内積は,随伴行列を用いて書くことが可能です。ここで,
\boldsymbol{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \quad \boldsymbol{b}= \begin{pmatrix} b_1\\ b_2 \\ \vdots \\ b_n \end{pmatrix}\in\mathbb{C}^n
に対して,この(複素)内積は,
と定義されます(→数ベクトルの定義と数ベクトルにおけるノルム・内積)。
随伴行列とベクトルの内積
\boldsymbol{a}, \boldsymbol{b}\in\mathbb{C}^n を列ベクトルとする。すなわち,
\boldsymbol{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \quad \boldsymbol{b}= \begin{pmatrix} b_1\\ b_2 \\ \vdots \\ b_n \end{pmatrix}
とする。このとき,ベクトルの(複素)内積について,
となる。
随伴行列(エルミート転置,共役転置)の性質10個
随伴行列は,転置行列の共役を取ったものですから,転置行列の定義と基本的な性質11個の証明で紹介した,基本的な性質と同じような性質が成立します。確認していきましょう。
一般の随伴行列の性質
定理(随伴行列の性質)
A, B を m \times n 行列とする。このとき,
- (A^*)^* = A.
- (A + B)^* = A^* + B^*.
- (kA)^* = \overline{k} A^*, \quad k \in\mathbb{C}.
また, A を m \times n 行列, B を n \times l 行列とすると,
- (AB)^* = B^* A^* .
上3つはほぼ明らかでしょう。最後の1つについては,両辺の各成分を比較することで確認するか,あるいは転置行列の定義と基本的な性質11個の証明で証明した, (AB)^\top = B^\top A^\top に対し,両辺共役を取ると考えればよいです。
正方行列における随伴行列
定理(随伴行列の性質2)
A を n 次正方行列とする。このとき,
- \operatorname{tr} A^* = \overline{\operatorname{tr} A}. (トレース)
- \det A^* = \overline{\det A} . (行列式)
- 随伴行列の固有値は,元の行列の固有値の複素共役である。
- \operatorname{rank} A^* = \operatorname{rank} A . (ランク)
- 列ベクトル \boldsymbol{v} , \boldsymbol{w} \in \mathbb{C}^n の(複素)内積について,
\langle A\boldsymbol{v}, \boldsymbol{w}\rangle = \langle \boldsymbol{v} , A^* \boldsymbol{w} \rangle. - A を正則(可逆行列)とすると,
(A^*)^{-1} = (A^{-1})^*.
それぞれ証明しておきましょう。
証明
1. \operatorname{tr} A^* = \overline{\operatorname{tr} A} について
\operatorname{tr} A^* = \sum_{k=1}^n \overline{a}_{kk} = \overline{\operatorname{tr} A} から従う。
2. \det A^* = \overline{\det A} について
行列式の定義式から, \det \overline{A} = \overline{\det A} である。加えて,転置行列の性質から, \det A^\top = \det A である。したがって,
\begin{aligned} \det A^* = \det \overline{A}^\top = \det \overline{A}=\overline{\det A} \end{aligned}
となる。
3. 随伴行列の固有値は,元の行列の固有値の複素共役であることについて
\begin{aligned} \det (\lambda I - A^*) &= \det (\overline{\lambda} I - A)^* \\ &= \overline{\det(\overline{\lambda} I - A^\top )} \end{aligned}
よりわかる(→固有値の定義と求め方をていねいに~計算の手順~)。ただし,2つ目の等式は上の2.を用いた。
4. \operatorname{rank} A^* = \operatorname{rank} A について
一次独立な数ベクトルの複素共役を取っても,一次独立なベクトルの数は変わらないことに注意する。
各列ベクトルに対する一次独立なものの個数と,各行ベクトルに対する一次独立なものの個数は等しく,これは階数 (rank) に一致していることから従う。
5. \langle A\boldsymbol{v}, \boldsymbol{w}\rangle = \langle \boldsymbol{v} , A^* \boldsymbol{w} \rangle について
\begin{aligned}\langle A\boldsymbol{v}, \boldsymbol{w}\rangle &=\sum_{i=1}^n \left( \sum_{k=1}^n a_{ik}v_k\right) \overline{w}_i \\ &=\sum_{i=1}^n \sum_{k=1}^n a_{ik}v_k\overline{w}_i \\ & = \sum_{k=1}^n \sum_{i=1}^n a_{ik}v_k\overline{w}_i \\ &=\sum_{k=1}^n v_k\overline{\left(\sum_{i=1}^n\overline{ a}_{ik}w_i\right)} \\ &=\langle \boldsymbol{v} , A^* \boldsymbol{w} \rangle. \end{aligned}
6. (A^*)^{-1} = (A^{-1})^* について
上の性質で述べた (AB)^* = B^* A^* を用いる。 I_n を n 次単位行列とすると,
\begin{gathered} (A^{-1})^* A^* = (A A^{-1})^* = I_n , \\ A^* (A^{-1})^* = (A^{-1} A)^* = I_n \end{gathered}
となり,これは (A^*)^{-1} =(A^{-1})^* を意味する。
証明終