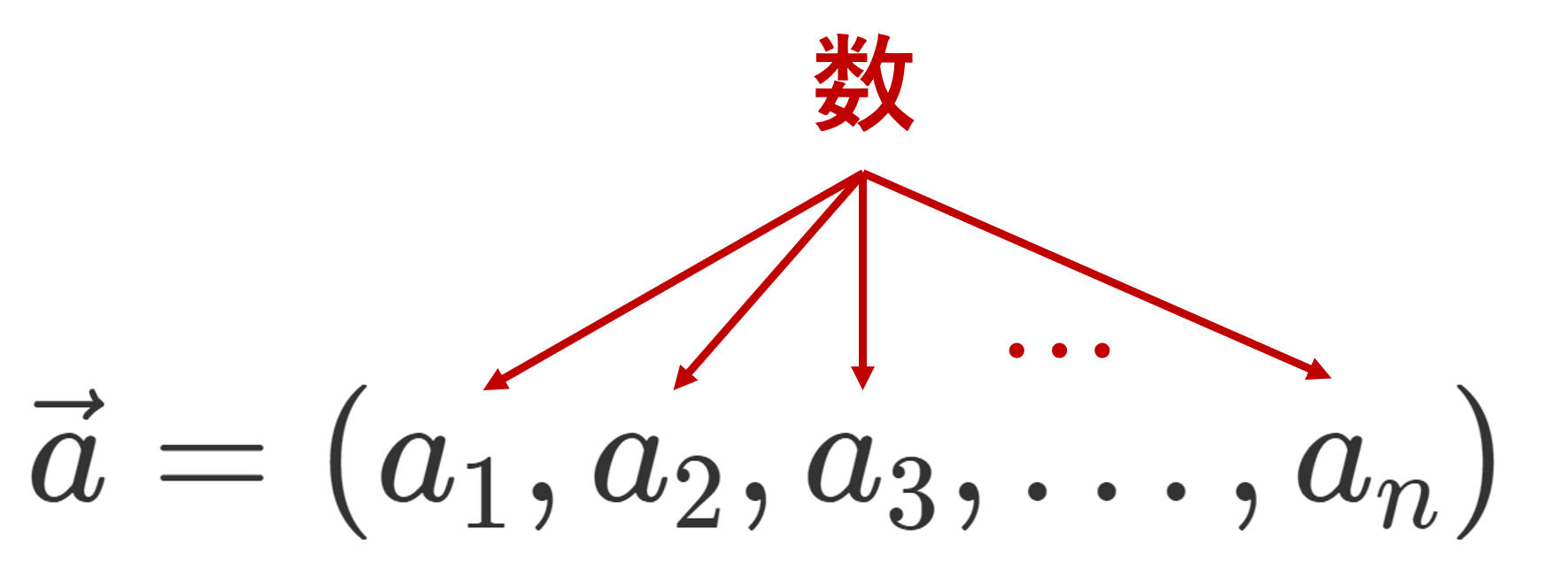
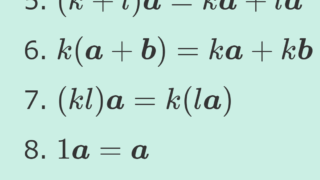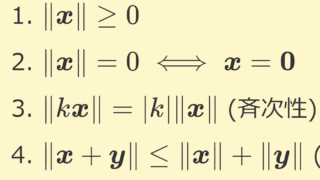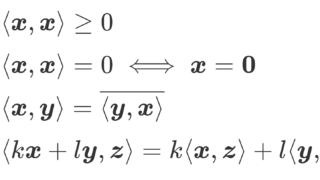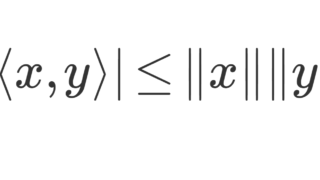数ベクトルとは,ざっくりいうと数を並べたものです。数を並べたものを「ベクトル」という一つのかたまりとして扱うことで,いろいろ便利なことがあるわけです。
今回は,「便利なこと」の紹介はしませんが,数ベクトルとは何かの定義とノルム・内積といった大切な概念を一気に解説しましょう。
数ベクトルの定義
実数を並べた数ベクトルと,複素数を並べた数ベクトルを順番に扱うことにしましょう。
実数上の数ベクトルの定義と具体例
定義(数ベクトル(実数版))
\color{red} \mathbb{R}^n =\{ (x_1, x_2, \dots, x_n)\mid x_k\in\mathbb{R}\}
とする。\boldsymbol{a}=(a_1, \dots, a_n), \boldsymbol{b}=(b_1, \dots, b_n)\in\mathbb{R}^n, \; k\in\mathbb{R} に対して,和・実数倍を
のように定義したとき, \mathbb{R}^n を \mathbb{R} 上 n 次元数ベクトル空間 (numerical vector space) といい,その各元を数ベクトル (numerical vector) という。
数ベクトルは \boldsymbol{a}\in\mathbb{R}^n のように太字で表しましたが, \vec{a}\in\mathbb{R}^n のように矢印をつけて表すこともあります。
数ベクトルは,高校でやったベクトルの延長になっています。具体例を通して,確認していきましょう。
数ベクトルの例1(平面ベクトル)
n=2 のとき, \mathbb{R}^2 =\{ (x_1,x_2)\mid x_1,x_2\in\mathbb{R}\} は平面ベクトルという。
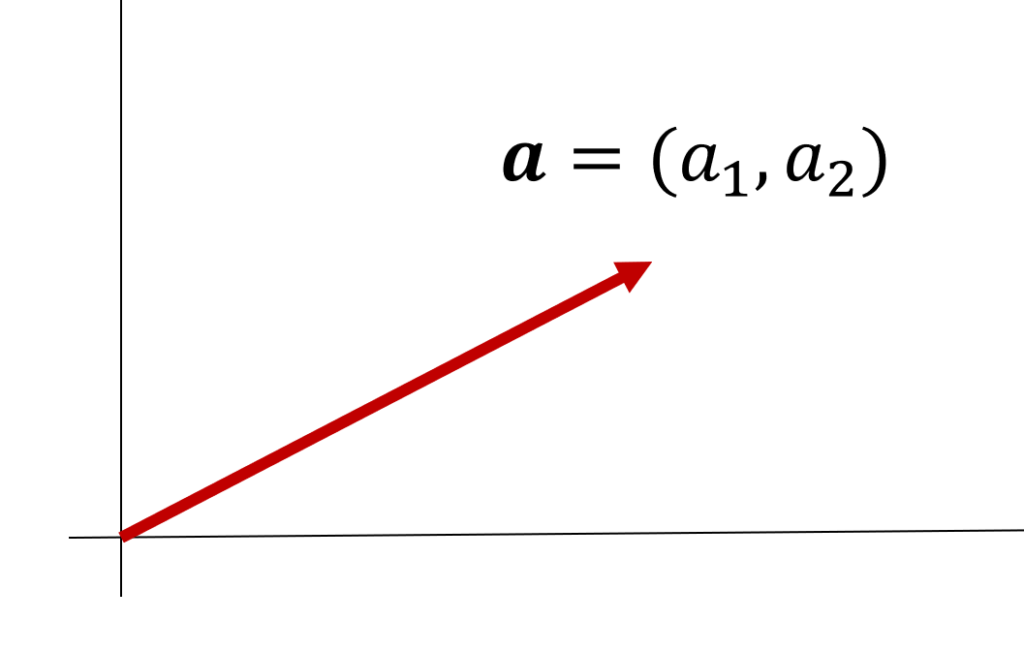
高校では \boldsymbol{a}=(a_1,a_2) と表すことを,平面ベクトルの「成分表示」と習ったのではないでしょうか。それですね。
数ベクトルの例2(空間ベクトル)
n=3 のとき, \mathbb{R}^3 =\{ (x_1,x_2,x_3)\mid x_1,x_2,x_3\in\mathbb{R}\} は空間ベクトルという。
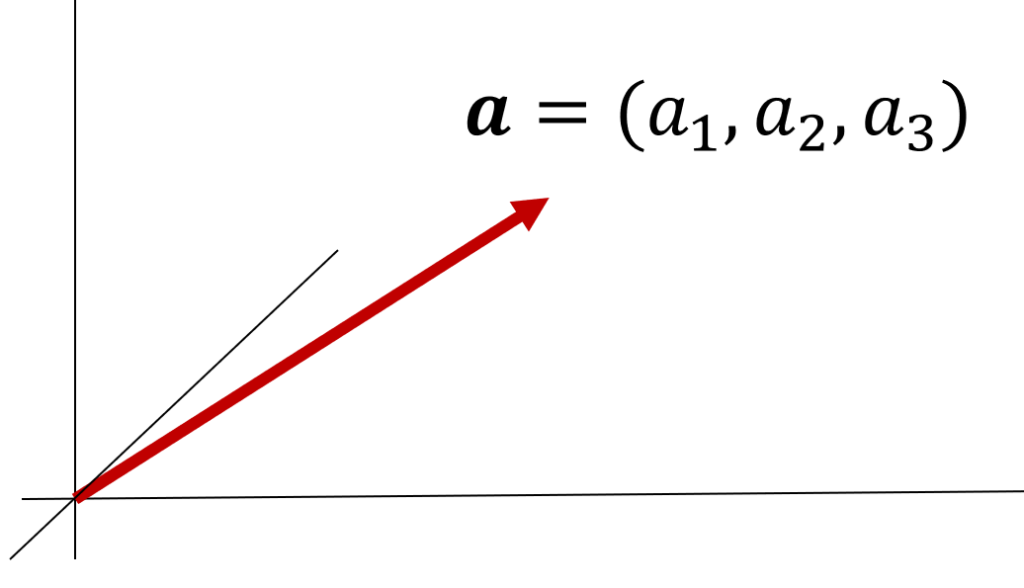
高校でいう,空間ベクトルの「成分表示」ですね。
なお,今回は横にかきましたが, \color{red} \boldsymbol{a}=\begin{pmatrix} a_1\\ \vdots \\ a_n\end{pmatrix} のように,縦にかくことも多いです。というかむしろ縦にかくことの方が多いです。横にかいたものを行ベクトル,縦にかいたものを列ベクトルといいます。
列ベクトルか行ベクトルかは,行列との演算を考える時に重要になってきます(→列ベクトルと行ベクトルの定義と違い)。
複素数上の数ベクトルの定義
続いて複素数上の数ベクトルです。実数と全く同じなのが分かるでしょう。
定義(数ベクトル(複素数版))
\color{red} \mathbb{C}^n =\{ (x_1, x_2, \dots, x_n)\mid x_k\in\mathbb{C}\}
とする。\boldsymbol{a}=(a_1, \dots, a_n),\boldsymbol{b}= (b_1, \dots, b_n)\in\mathbb{C}^n, \; k\in\mathbb{C} に対して,和・実数倍を
のように定義したとき, \mathbb{C}^n を \mathbb{C} 上 n 次元数ベクトル空間 (numerical vector space) といい,その各元を数ベクトル (numerical vector) という。
線形代数学や専門数学では,複素数の数ベクトルを扱うことも多いでしょう。一方で,情報系の場合は実数の数ベクトルの方がよく扱うかもしれません。
数ベクトルの性質
数ベクトルの性質として大事なのは,以下の性質です。
\boldsymbol{a},\boldsymbol{b},\boldsymbol{c} \in\mathbb{R}^n (または \mathbb{C}^n )とし,さらに \boldsymbol{0} = (0,\dots, 0),\; k,l\in\mathbb{R}(または \mathbb{C})とするとき,
- (\boldsymbol{a} + \boldsymbol{b} ) + \boldsymbol{c} = \boldsymbol{a} + (\boldsymbol{b} + \boldsymbol{c})
- \boldsymbol{a} + \boldsymbol{b} = \boldsymbol{b} +\boldsymbol{a}
- \boldsymbol{a} + \boldsymbol{0} = \boldsymbol{0} + \boldsymbol{a} = \boldsymbol{a}
- \boldsymbol{a} + (-\boldsymbol{a}) = (-\boldsymbol{a}) + \boldsymbol{a} = \boldsymbol{0}
- (k + l) \boldsymbol{a} = k \boldsymbol{a} + l \boldsymbol{a}
- k (\boldsymbol{a} + \boldsymbol{b}) = k \boldsymbol{a} + k \boldsymbol{b}
- (kl)\boldsymbol{a} = k (l \boldsymbol{a})
- 1\boldsymbol{a}=\boldsymbol{a}
どれも当たり前に思うかもしれませんね。より専門的な数学では,「数ベクトル」は拡張され,一般の「ベクトル空間」と呼ばれるものを扱うようになります。このときに大事になってくるのが上の8つの性質です。
数ベクトルにおけるノルム・内積
ノルムとは,ベクトルの大きさのことです。内積とは,ベクトルの類似度を評価する指標です。
数ベクトルには,ノルムや内積が定義できます。定義を述べましょう。
実数上の数ベクトルにおけるノルム・内積
ここで述べるのは,最も標準的なノルム・内積です。
定義(数ベクトル上のノルム・内積(実数版))
\boldsymbol{a}=(a_1,\dots, a_n) \in\mathbb{R}^n に対し,
\color{red} \lVert \boldsymbol{a}\rVert = \sqrt{\sum_{k=1}^n a_k^2 } = \sqrt{a_1^2+\dots a_n^2}
を \boldsymbol{a} のノルム (norm) という。また, \boldsymbol{a}=(a_1,\dots, a_n) ,\boldsymbol{b}=(b_1,\dots, b_n) \in\mathbb{R}^n に対し,
を \boldsymbol{x},\boldsymbol{y} の内積 (inner product) という。
定義から,
\lVert\boldsymbol{a}\rVert =\sqrt{\langle\boldsymbol{a},\boldsymbol{a}\rangle }
のように,ノルムは内積を使って表せますね。逆に,内積もノルムを使って
と表すことができます(polarization identity)。
さらに,一般に |\langle\boldsymbol{a},\boldsymbol{b}\rangle| \le \lVert \boldsymbol{a}\rVert\lVert \boldsymbol{b}\rVert が知られています。これをコーシーシュワルツの不等式といいます。
なお,内積は \color{red}\langle \boldsymbol{a},\boldsymbol{b}\rangle 以外に,\color{red} \boldsymbol{a}\cdot \boldsymbol{b} や \color{red} (\boldsymbol{a},\boldsymbol{b} ) などとかくこともあります。物理では,高校と同じドットを使った表記が多いかもしれませんね。
ノルム・内積の例1(平面ベクトル)
\boldsymbol{a}=(a_1,a_2),\boldsymbol{b}=(b_1,b_2)\in\mathbb{R}^2 において,
\begin{aligned} \lVert \boldsymbol{a}\rVert &= \sqrt{a_1^2+a_2^2},\\ \langle\boldsymbol{a},\boldsymbol{b}\rangle &= a_1b_1+a_2b_2 \end{aligned}
である。 \boldsymbol{a},\boldsymbol{b} のなす角を \theta とすると, \langle\boldsymbol{a},\boldsymbol{b}\rangle = \lVert \boldsymbol{a}\rVert \lVert \boldsymbol{b}\rVert\cos\theta になっている。
高校では |\vec{a}|, \;\vec{a}\cdot \vec{b} みたいな書き方をしていたと思います。 大学では,大きさの方に関しては絶対値と区別して,縦棒を二本かくのが普通です。
ノルム・内積の例2(空間ベクトル)
\boldsymbol{a}=(a_1,a_2,a_3),\boldsymbol{b}=(b_1,b_2,b_3)\in\mathbb{R}^2 において,
\begin{aligned} \lVert \boldsymbol{a}\rVert &= \sqrt{a_1^2+a_2^2+a_3^2},\\ \langle\boldsymbol{a},\boldsymbol{b}\rangle &= a_1b_1+a_2b_2+a_3b_3 \end{aligned}
である。
複素数の数ベクトルにおけるノルム・内積
続いて複素数の数ベクトルにおけるノルム・内積です。実数のときとの違いに注意しましょう。
定義(数ベクトル上のノルム・内積(複素数版))
\boldsymbol{a}=(a_1,\dots, a_n) \in\mathbb{C}^n に対し,
\color{red} \lVert \boldsymbol{a}\rVert = \sqrt{\sum_{k=1}^n |a_k|^2 } = \sqrt{|a_1|^2+\dots |a_n|^2}
を \boldsymbol{a} のノルム (norm) という。また, \boldsymbol{a}=(a_1,\dots, a_n) ,\boldsymbol{b}=(b_1,\dots,b_n) \in\mathbb{C}^n に対し,
を \boldsymbol{a},\boldsymbol{b} の内積 (inner product) という。
\overline{b}_k は, b_k の複素共役を表します。複素数のときは,内積は複素共役を取るんですね。こうした方がノルムと内積の関係が実数と同じになります。実際,
\lVert\boldsymbol{a}\rVert =\sqrt{\langle\boldsymbol{a},\boldsymbol{a}\rangle }
のように,ノルムは内積を使って表せますね。逆に,内積もノルムを使って
と表すことができます(polarization identity)。
さらに実数の場合と同様に,コーシーシュワルツの不等式 |\langle\boldsymbol{a},\boldsymbol{b}\rangle| \le \lVert \boldsymbol{a}\rVert\lVert \boldsymbol{b}\rVert が成立します。
ノルム・内積の性質
ノルム・内積で大事な性質は以下です。
\boldsymbol{a},\boldsymbol{a_1},\boldsymbol{a_2},\boldsymbol{b}\in\mathbb{R}^n または \mathbb{C}^n とし, k\in\mathbb{R} または \mathbb{C} とする。このとき,
- \lVert \boldsymbol{a} \rVert \ge 0
- \lVert \boldsymbol{a} \rVert = 0\iff \boldsymbol{a}=\boldsymbol{0}
- \lVert \boldsymbol{a}+\boldsymbol{b} \rVert \le \lVert \boldsymbol{a} \rVert +\lVert \boldsymbol{b} \rVert
- \langle \boldsymbol{a},\boldsymbol{a}\rangle\ge 0
- \langle \boldsymbol{a},\boldsymbol{a}\rangle= 0\iff \boldsymbol{a}=\boldsymbol{0}
- \langle \boldsymbol{a_1} +\boldsymbol{a_2},\boldsymbol{b}\rangle = \langle \boldsymbol{a_1} ,\boldsymbol{b}\rangle + \langle \boldsymbol{a_2},\boldsymbol{b}\rangle
- \langle k \boldsymbol{a} ,\boldsymbol{b}\rangle= k \langle \boldsymbol{a},\boldsymbol{b}\rangle
- \langle\boldsymbol{a},\boldsymbol{b}\rangle =\overline{\langle\boldsymbol{b},\boldsymbol{a}\rangle}
これらは,数ベクトル以外の一般のノルム・内積を定めるときに,定義として使われるものです。なんとなくでいいので知っておくとよいでしょう。
なお,2つのベクトルの内積が 0 であるとき,2つのベクトルは直交するといいます。
ノルム・内積に関するより一般的な話は,以下の記事で扱っています。
標準基底(自然な正規直交基底)
ベクトル空間 \mathbb{R}^n または \mathbb{C}^n において,
\begin{aligned}\boldsymbol{e_1} &= (1,0,0,\dots, 0)\\ \boldsymbol{e_2} &= (0,1,0,\dots, 0)\\ \boldsymbol{e_3} &= (0,0,1,\dots, 0)\\ &\vdots \\ \boldsymbol{e_n} &=(0,0,0,\dots , 1)\end{aligned}
としたときの \boldsymbol{e_1},\boldsymbol{e_2},\dots, \boldsymbol{e_n} は専門用語で「正規直交基底」になっています。これを,標準基底といいます。
「正規」とはノルムが 1 であることを指し,「直交」とは互いの内積が 0 であることを指し,「基底」とは,簡単に言うと「これらのベクトルを使えばすべてのベクトルがただ一通りに表せる」という意味です。
標準基底はよく使われるので覚えておくとよいでしょう。