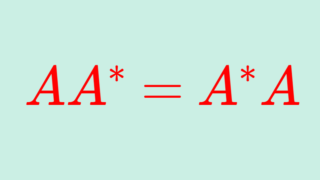対称行列の定義と性質4つとその証明

対称行列とは， $A=A^\top$ が成立する行列を指します。対称行列の定義・性質4つを紹介しましょう。

対称行列の定義
対称行列の性質4つとその証明
その他の行列

対称行列の定義

定義（対称行列）

$n$ 次正方行列 $A$ について，

\Large \color{red} A^\top = A

が成立するとき， $A$ を対称行列 (symmetric matrix) という。

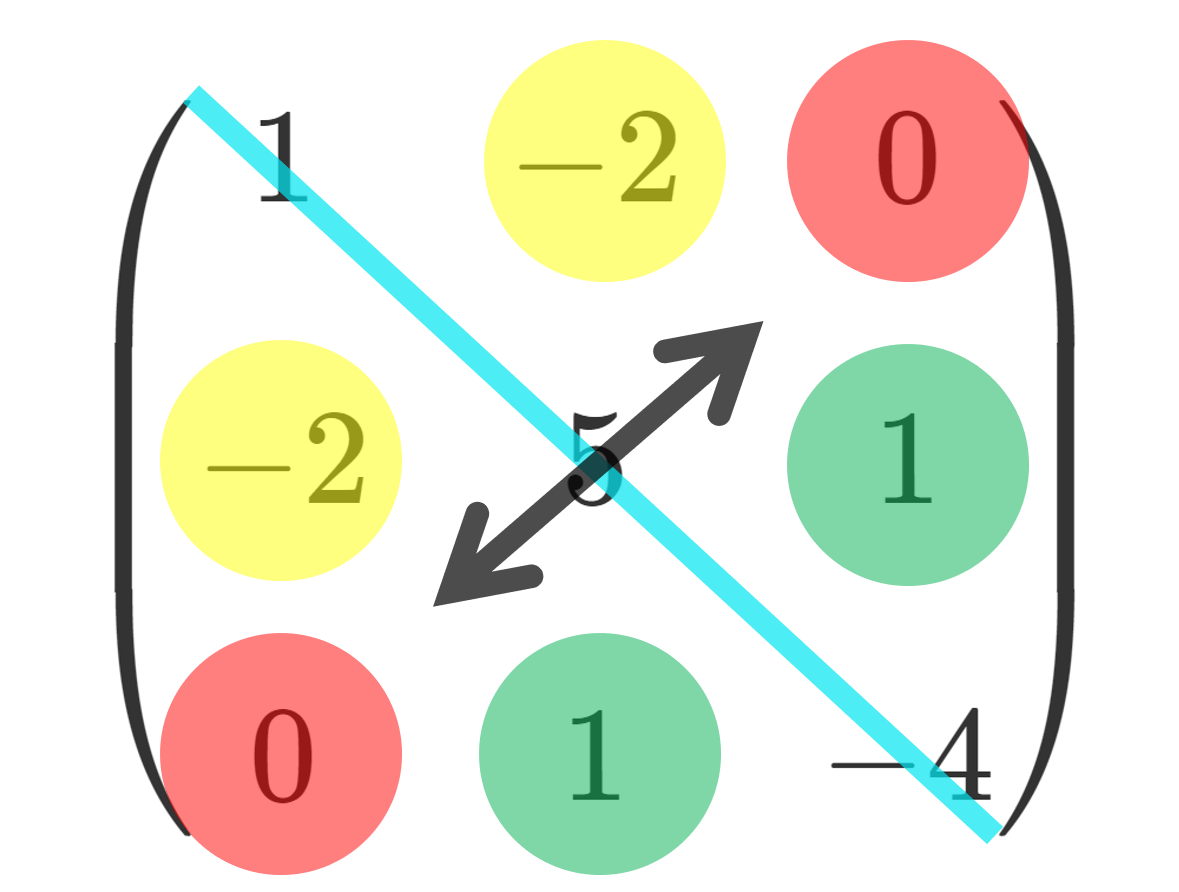
$A^\top$ は $A$ の「転置行列」の意味です(→転置行列の定義と基本的な性質11個の証明)。転置行列と元の行列が一致するような行列を対称行列というんですね。

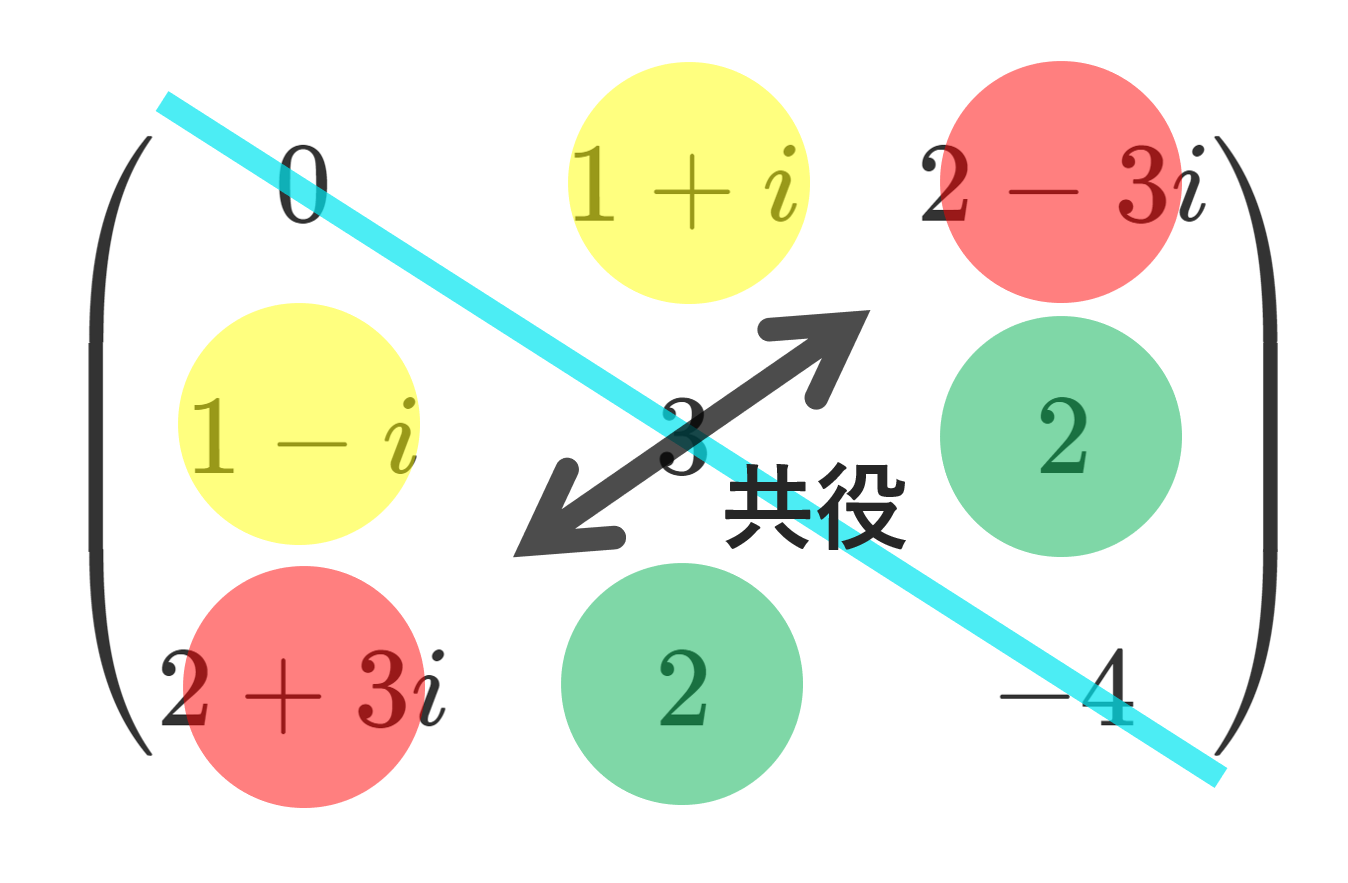
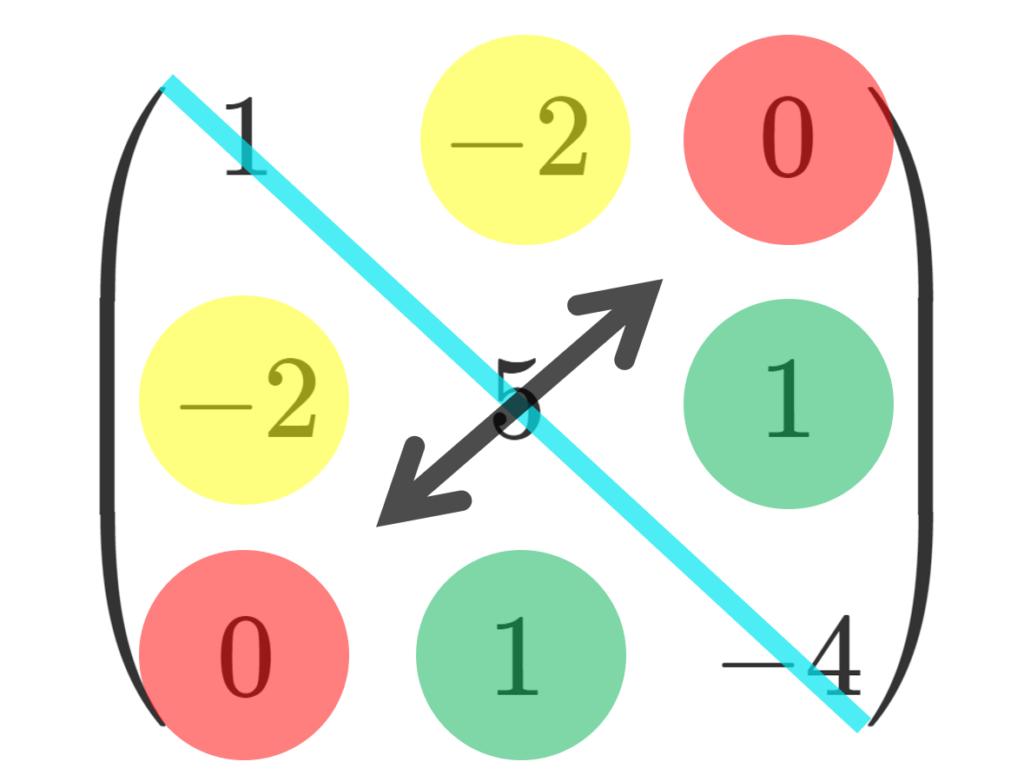
いくつか具体例を紹介しておきましょう。

対称行列の例

$\begin{pmatrix}1 & 3 \\ 3 & 0 \end{pmatrix}$
$\begin{pmatrix} 1 & -2 & 0 \\ -2& 5 & 1\\ 0 & 1 & -4\end{pmatrix}$
$\begin{pmatrix} 1&2&3&4\\2&3&4&5\\ 3&4&5&6\\ 4&5&6&7\end{pmatrix}$
零行列
単位行列
対角行列

対称行列の性質4つとその証明

定理（対称行列の性質）

$A$ を正方行列とするとき， $\color{red}A+A^\top, \; AA^\top$ は対称行列になる。
$A$ を実対称行列とするとき， $\boldsymbol{x}, \boldsymbol{y}\in \mathbb{C}^n$ を列ベクトルとすると，内積について $\color{red} \langle A\boldsymbol{x}, \boldsymbol{y}\rangle=\langle \boldsymbol{x},A\boldsymbol{y}\rangle$ が成り立つ。
実対称行列の固有値は全て実数である。
実対称行列 $A$ は実直交行列 $P$ により対角化可能である。すなわち， $T=P^{-1}AP$ が対角行列にできる。

「実対称行列は直交行列により対角化可能」より $AP=PT$ となり，これを言い換えると固有ベクトルが直交していることを意味します。これも大切な性質です。

さらに，実対称行列は $AA^*=A^*A$ (ただし $A^*=\overline{A}^\top$ は随伴行列(共役転置)) も成り立ちますから，正規行列の一種です。したがって，正規行列で成立する性質もすべて成立します。これについては，以下で解説しています。

1. A+A^T, AA^T が対称行列になること

証明

\begin{aligned}&(A+A^\top)^\top = A^\top+ (A^\top)^\top \\&= A^\top+A=A+A^\top \end{aligned}

より， $A+A^\top$ は対称行列である。また，積と転置行列の性質より，

(AA^\top)^\top = (A^\top)^\top A^\top = AA^\top

より， $AA^\top$ は対称行列である。

証明終

任意の正方行列 $A$ に対して，

A=\frac{1}{2}(A+A^\top)+\frac{1}{2}(A-A^\top)

であり， $(A+A^\top)/2, (A-A^\top)/2$ はそれぞれ対称行列・交代行列とですから，任意の行列は対称行列と交代行列の和に分解できることになります。

2. <Ax,y>=<x,AY>であること

証明

$A$ を実対称行列とすると， $A^*=A$ (随伴行列(共役転置))である。内積について， $\langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^*\boldsymbol{y}\rangle$ である(→随伴行列(エルミート転置,共役転置)の定義と性質10個)から，題意は示された。

証明終

3. 実対称行列の固有値は実数であること

証明

$\lambda\in\mathbb{C}$ を固有値， $\boldsymbol{x}$ をそれに対応する固有ベクトルとすると， $A\boldsymbol{x}=\lambda \boldsymbol{x}$ である。性質2.より， $\langle A\boldsymbol{x},\boldsymbol{x}\rangle = \langle \boldsymbol{x},A\boldsymbol{x}\rangle$ であるので，

\lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle = \overline{\lambda} \langle\boldsymbol{x},\boldsymbol{x}\rangle .

すなわち $(\lambda -\overline{\lambda})\lVert \boldsymbol{x}\rVert^2=0$ であり， $\lambda =\overline{\lambda}.$ これは $\lambda$ が実数であることを意味する。

証明終

途中で用いたのは内積の共線形性ですね。 $\langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle = \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle ,\; \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle =\overline{ \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{ \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle$ です。