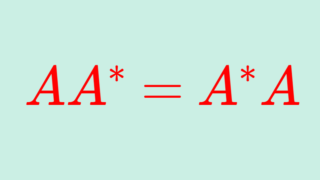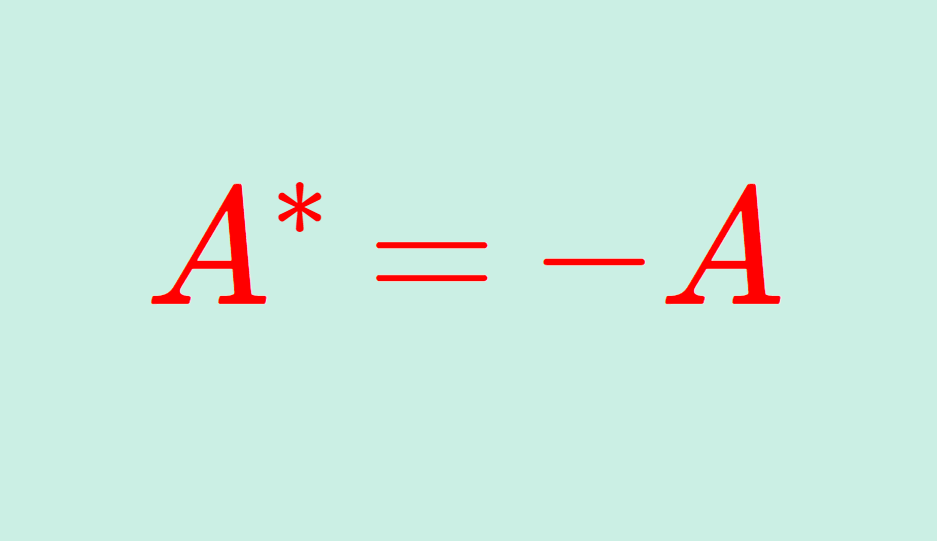交代行列とは,転置行列が元の行列の -1 倍になる行列,すなわち A^\top =-A をみたす行列を指します。
交代行列の定義と,重要な性質を紹介しましょう。
交代行列の定義
A^\top は A の転置行列を指します(→転置行列の定義と基本的な性質11個の証明)。交代行列とは,転置行列が元の行列の -1 倍になる行列を言うんですね。
なお, A^\top=A のように,-1 倍しない行列は対称行列といいます。これは,対称行列の定義と性質4つとその証明で解説しています。
交代行列の具体例
交代行列の具体例
- \begin{pmatrix} 0 & 1 \\ -1&0 \end{pmatrix}
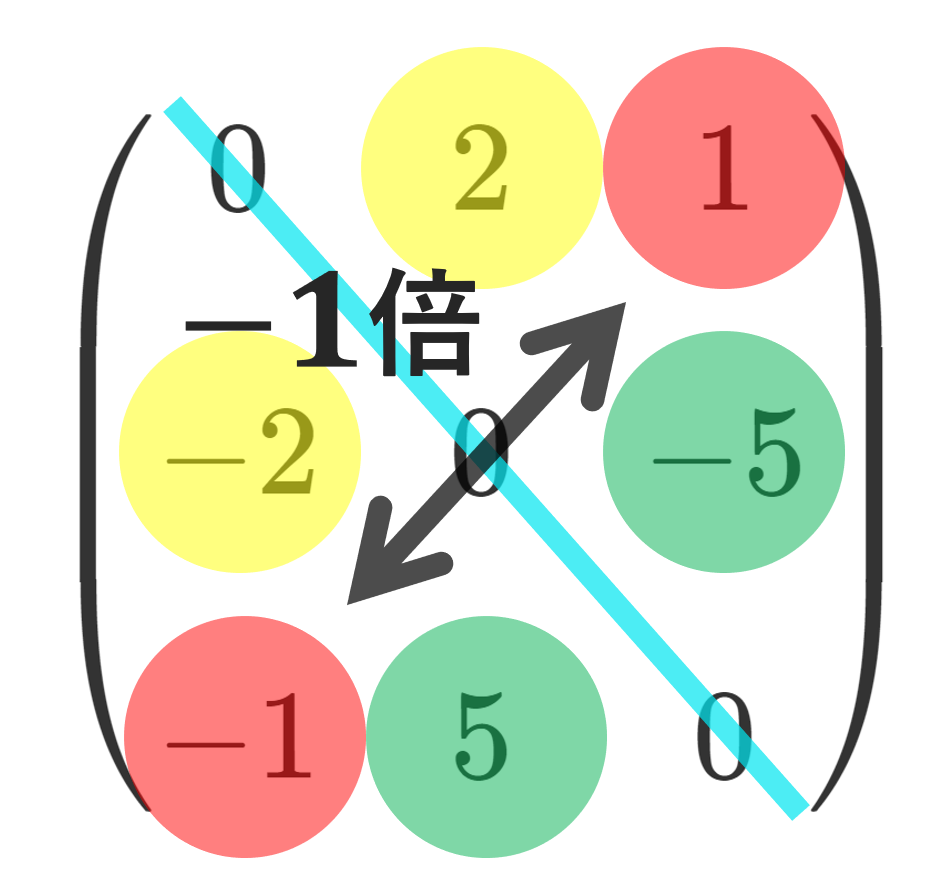
- \begin{pmatrix} 0& 2 & 1 \\ -2 & 0 & -5 \\ -1 & 5& 0\end{pmatrix}
- 零行列
交代行列の重要な性質5つ
定理(交代行列の性質)
なお,実交代行列は AA^* = -A^2=A^* A (ただし A^* = \overline{A}^\top は随伴行列(共役転置))をみたすため,正規行列 (normal matrix) です。よって,正規行列で成り立つ性質の全てが成立します。たとえば,交代行列は対角化可能です。正規行列の性質については,以下で解説しています。
さて,定理を順番に証明していきましょう。
1. 交代行列の対角成分は0
証明
A=(a_{ij}) を交代行列とすると,A^\top = -A より a_{ii}=-a_{ii} なので a_{ii}=0.
証明終
2. A-A^T は交代行列
証明
(A-A^\top)^\top = A^\top -(A^\top)^\top = -(A-A^\top)
より, A-A^\top は交代行列である。
証明終
任意の正方行列は
A=\frac{1}{2}(A+A^\top)+\frac{1}{2}(A-A^\top)
とできるため,対称行列と交代行列の和に分解することが可能です。
3. 奇数次の交代行列の行列式は0
証明
一般に正方行列に対して \det A =\det A^\top に注意する(→転置行列の定義と基本的な性質11個の証明)。
\det A= \det A^\top = \det (-A)= (-1)^n\det A
より,n が奇数ならば \det A=-\det A. よって, \det A=0.
証明終
よって特に奇数次の交代行列は正則行列(可逆行列)ではありません。
4. 実交代行列なら<Ax,y>=-<x,Ay>
証明
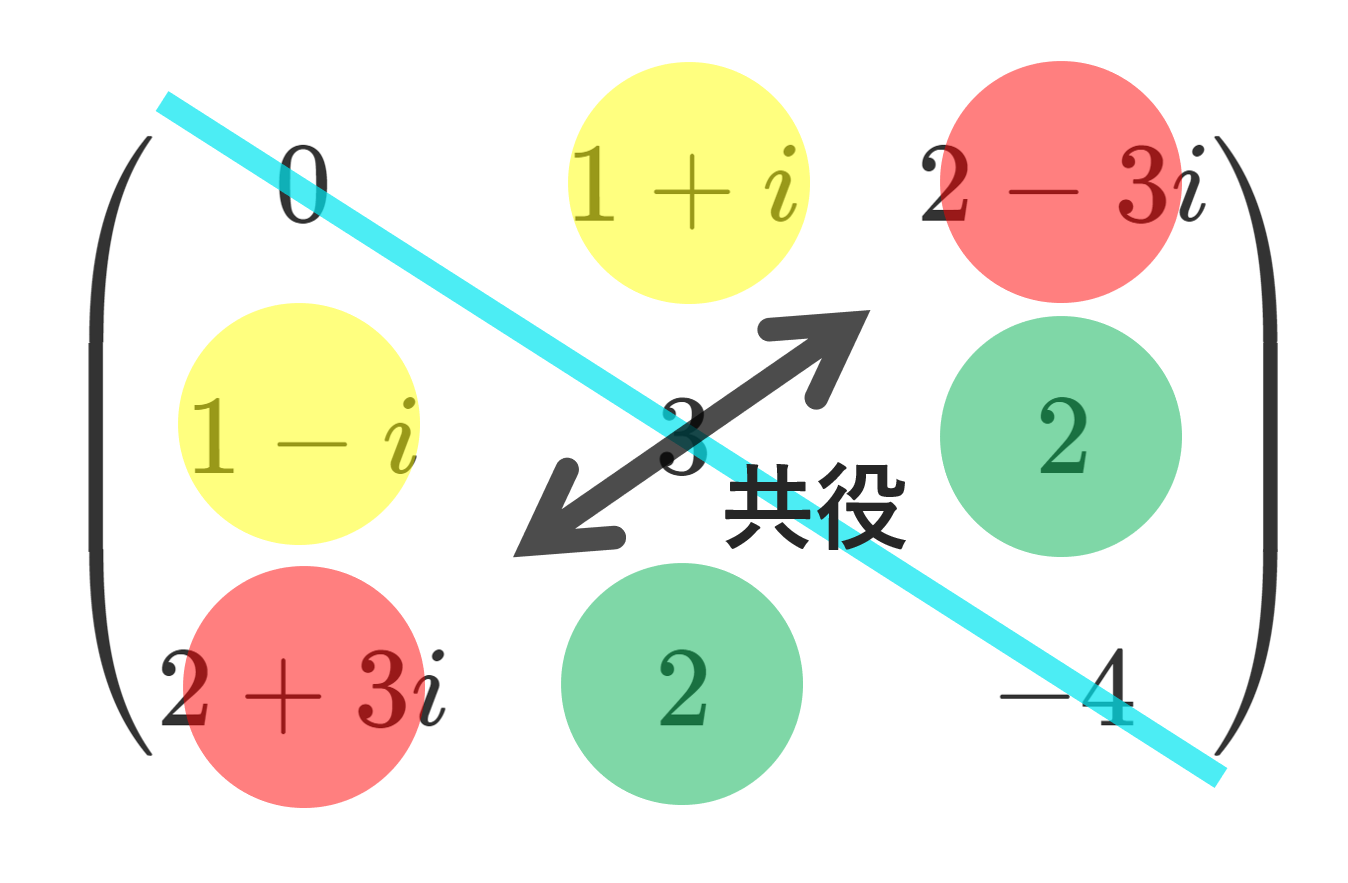
一般に正方行列 A について,\langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^*\boldsymbol{y}\rangle であることに注意する(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。ただし, A^* = \overline{A}^\top は随伴行列(共役転置)である。
今の場合, A^* = A^\top =-A なので,
\langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x},-A\boldsymbol{y}\rangle =- \langle \boldsymbol{x},A\boldsymbol{y}\rangle.証明終
5. 実交代行列の固有値は純虚数または0
証明
\lambda\in\mathbb{C} を実交代行列 A の固有値とし,\boldsymbol{x} をそれに対応する列ベクトルとする。このとき, A\boldsymbol{x}=\lambda \boldsymbol{x} である。性質4.より, \langle A\boldsymbol{x},\boldsymbol{x}\rangle = -\langle \boldsymbol{x},A\boldsymbol{x}\rangle が成立するので。
\langle \lambda \boldsymbol{x},\boldsymbol{x}\rangle =- \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle .
すなわち, \langle \lambda \boldsymbol{x},\boldsymbol{x}\rangle =-\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle,すなわち (\lambda+\overline{\lambda})\lVert \boldsymbol{x}\rVert^2=0 なので, \lambda+\overline{\lambda} =0. これは \lambda は純虚数または 0 である。
証明終
途中で用いたのは内積の共線形性ですね。 \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle = \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle ,\; \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle =\overline{ \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{ \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle です。