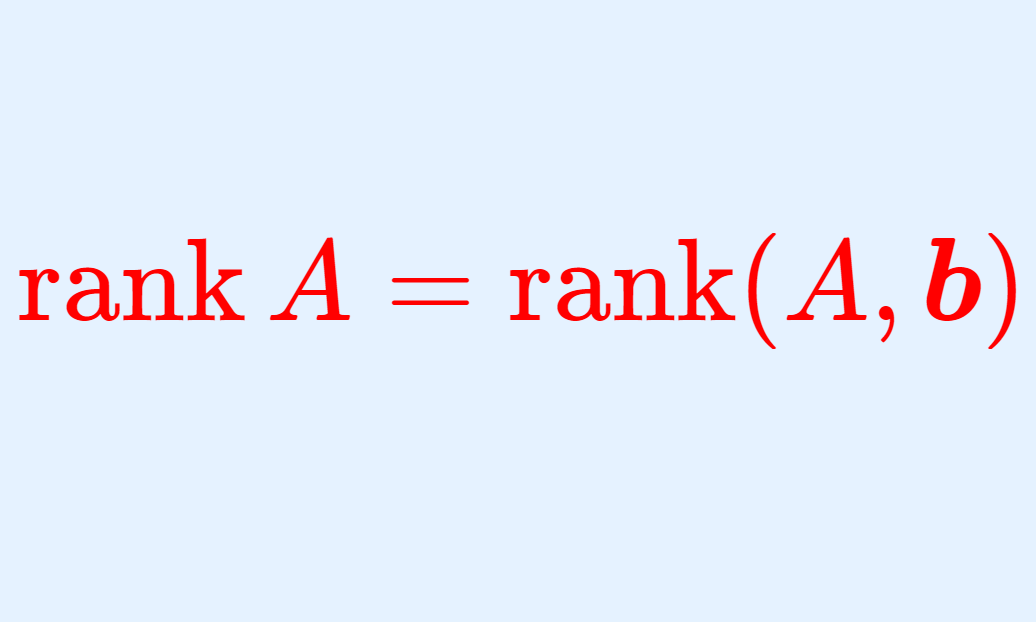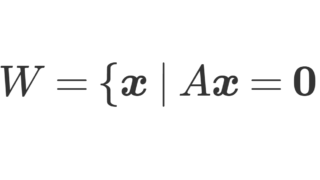連立一次方程式は,行列を用いて記述することができ,それが解をもつかどうかは,行列のランクを用いて記述することができます。この定理について紹介し,証明しましょう。
後半では,解が「ただ一つ」になる必要十分条件も扱います。
連立一次方程式が解をもつ条件(行列)
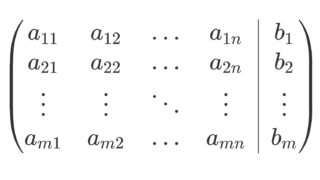
連立一次方程式
\begin{cases} a_{11}x_1+a_{12}x_2+\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots + a_{2n}x_n = b_2 \\ \ldots \\ a_{m1}x_1+a_{m2}x_2+\cdots + a_{mn}x_n = b_m \end{cases}
は,行列を用いて表すと
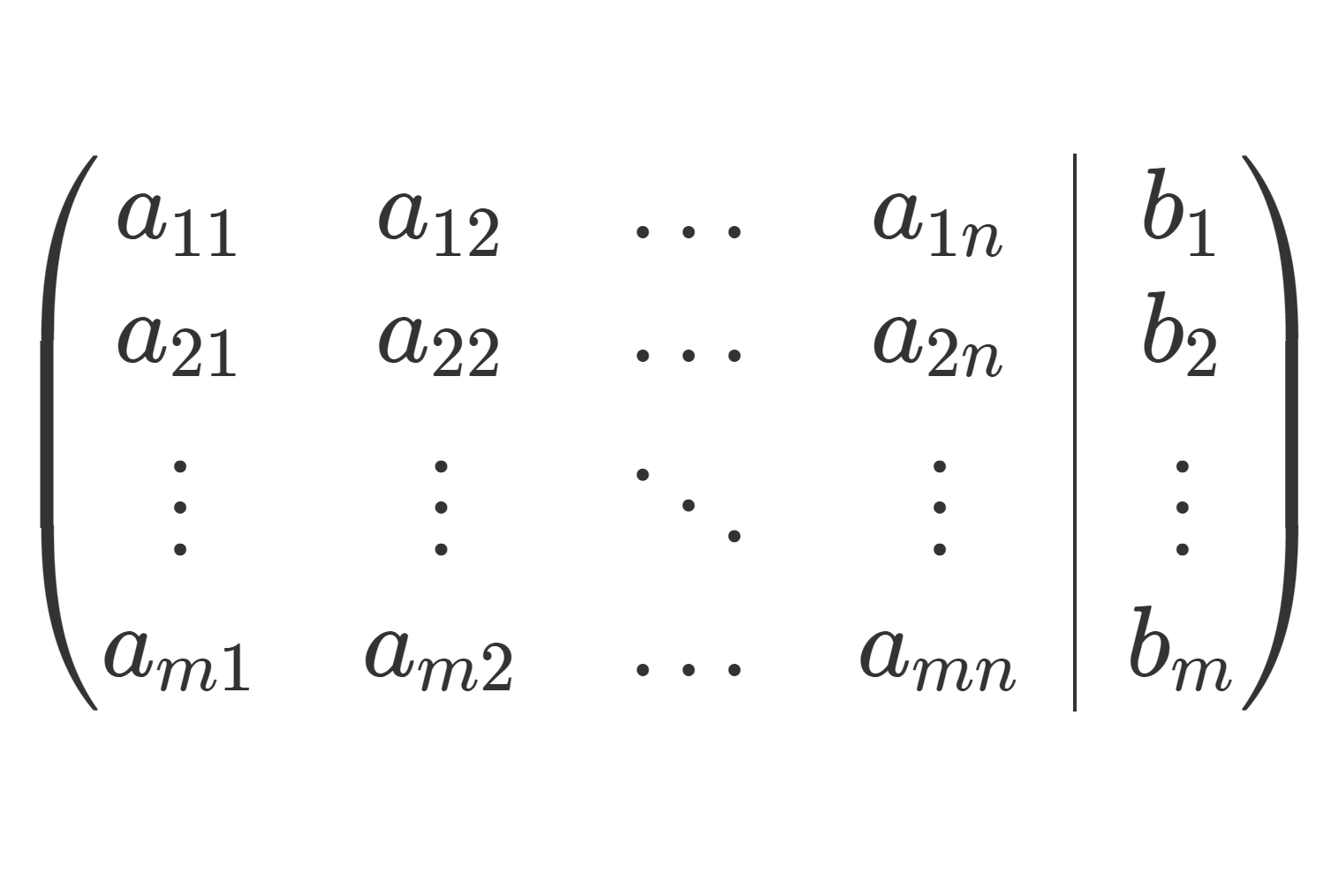
とかけます。この式に対応して, A\boldsymbol{x} = \boldsymbol{b} とかくことにしましょう。このとき, A を係数行列, A に \boldsymbol{b} をくっつけた行列 (A,\boldsymbol{b}) を拡大係数行列といいます。詳しくは,以下で解説しています。
これらを用いて,連立一次方程式が解をもつ必要十分条件を与えましょう。
連立一次方程式が解をもつ条件(行列)
定理(連立一次方程式が解をもつ条件(行列))
連立一次方程式 A\boldsymbol{x} = \boldsymbol{b} が解をもつ必要十分条件は
\color{red}\operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b})
が成立することである。
ここで, \operatorname{rank} については,以下の記事で解説しています。
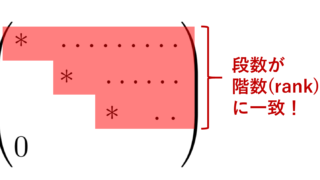
ランクは行基本変形で階段行列にすることで求められます。
連立一次方程式が解をもつかの判定は, A と (A,\boldsymbol{b}) のランクを求めればよいことになります。
A のランクは, (A, \boldsymbol{b}) のランクを求める過程で同時に求まりますから,実際は (A, \boldsymbol{b}) のランクのみ求めればよいです。
連立一次方程式が解をもつ条件(行列)の証明
上の定理を早速証明しておきましょう。
証明
以下, A = (\boldsymbol{a_1}, \boldsymbol{a_2}, \dots, \boldsymbol{a_n}),\; \boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n\end{pmatrix} とする。
解をもつ \implies \operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b}) について
A\boldsymbol{x} = \boldsymbol{b} が解をもつ,すなわちこの式をみたす \boldsymbol{x} が存在するとき,この式を書き直すと,
x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+\dots +x_n \boldsymbol{a_n} = \boldsymbol{b}
となる。特に, \boldsymbol{b} が \boldsymbol{a_1}, \boldsymbol{a_2},\dots,\boldsymbol{a_n} の一次結合でかけている。ランクの定義は,一次独立な列ベクトルの最大個数であるから,\operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b}) である。
\operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b}) \implies 解をもつについて
ランクの定義は,一次独立な列ベクトルの最大個数である。特に, \operatorname{rank}A = m とすると, \boldsymbol{a_1},\boldsymbol{a_2},\dots, \boldsymbol{a_n} から, m 個の一次独立なベクトルが選べる。仮定より, \boldsymbol{b} は,選んだ m 個の一次独立なベクトルの一次結合で表せる。特に,
\boldsymbol{b}=x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+\dots +x_n \boldsymbol{a_n}
となる \boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n\end{pmatrix} が存在する。これは, A\boldsymbol{x} =\boldsymbol{b} を意味し,解をもつことが分かった。
証明終
連立一次方程式がただ一つ解をもつ条件(行列)
先ほどは単に「解をもつ」を考えましたが,次に,「解がただ一つ」である必要十分条件を考えてみましょう。
連立一次方程式がただ一つ解をもつ条件(行列)
定理(連立一次方程式がただ一つ解をもつ条件(行列))
A を m\times n 行列, \boldsymbol{b}\in \mathbb{R}^m とする。
このとき,連立一次方程式 A\boldsymbol{x} = \boldsymbol{b} がただ一つの解 \boldsymbol{x}\in \mathbb{R}^n をもつ必要十分条件は
が成立することである。特に, m\ge n でなければならない。
さっきの定理から「=n」の部分が追加されましたね。
最後の「 m\ge n でなければならない」については,結論とランクの性質より,
n=\operatorname{rank} A \le \min\{m, n\}
であることから従います。 m\ge n とは要するに,連立方程式の式の本数は,変数の数以上であるということです。
早速証明しておきましょう。
連立一次方程式がただ一つ解をもつ条件(行列)の証明
解の存在 \iff \operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b}) はすでに証明済みですから,示すべきは,解の存在の下で,解の一意性 \iff \operatorname{rank} A =n ですね。
証明
記号は,前の証明と同じものを用いる。
解がただ一つ \implies \operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b})=n について
仮定より,
x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+\dots +x_n \boldsymbol{a_n} = \boldsymbol{b} \tag{1}
をみたす x_1, x_2,\dots, x_n がただ一つである。これは, \boldsymbol{a_1}, \boldsymbol{a_2},\dots, \boldsymbol{a_n} が一次独立であることを示している。実際,一次独立でない,すなわち
をみたす (k_1, k_2, \dots, k_n ) \ne \boldsymbol{0} が存在すると仮定すると, (1), (2) の辺々足し合わせることで, \boldsymbol{x'} = \begin{pmatrix} x_1+k_1 \\ x_2+k_2 \\ \vdots \\ x_n + k_n \end{pmatrix} も連立方程式の解になり,解の一意性に反するからである。
ランクの定義は,一次独立な列ベクトルの最大個数であったから, \operatorname{rank} A =n である。
\operatorname{rank} A = \operatorname{rank}(A,\boldsymbol{b})=n \implies 解がただ一つについて
2つの解を \boldsymbol{x^{(1)}}, \boldsymbol{x^{(2)}} とおく。これが一致していることを示せばよい。 A\boldsymbol{x^{(1)}} =\boldsymbol{b}, \; A\boldsymbol{x^{(2)}} = \boldsymbol{b} の辺々引くと,
A(\boldsymbol{x^{(1)}} - \boldsymbol{x^{(2)}} ) =\boldsymbol{0}
となる。これを展開すると,
である。ランクの定義は,一次独立な列ベクトルの最大個数より, \operatorname{rank} A=n の仮定から, \boldsymbol{a_1}, \boldsymbol{a_2},\ldots, \boldsymbol{a_n} は一次独立である。すなわち,
となるから, \boldsymbol{x^{(1)}} = \boldsymbol{x^{(2)}} を得る。
証明終