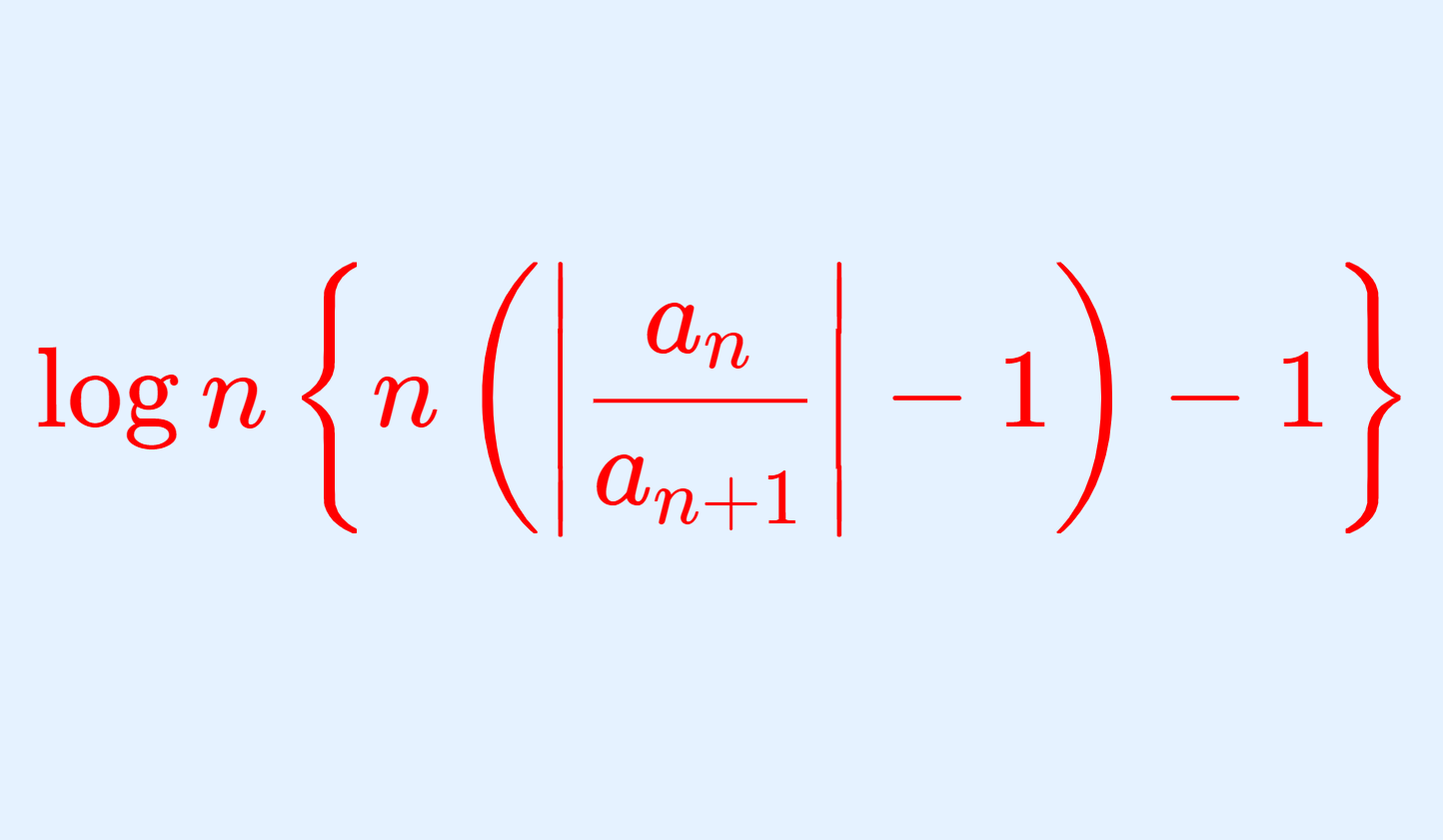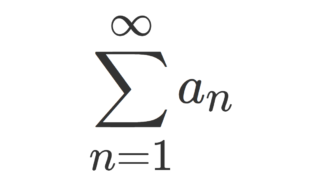【級数の収束判定法】Bertrand’s testとは

$\sum 1/r^n$ と比較するダランベールの収束判定法・コーシーの収束判定法や， $\sum 1/n^p$ と比較するラーベの収束判定法・ガウスの収束判定法でも判定できないものを判定する方法の一つとして，「Bertrandの収束判定法」というものがあります。

これについて，その内容と証明を紹介しましょう。

定理（Bertrandの判定法; Bertrand’s test）

$0$ にならない数列 $\{ a_n\}$ が

\color{red} \left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{1}{n} + \frac{c_n}{n\log n}

と表せるとする。すなわち，

\color{red} c_n = (\log n) \left\{n\left( \left|\frac{a_n}{a_{n+1}}\right| - 1 \right) - 1\right\}

である。このとき，

$\color{red}\displaystyle\liminf_{n\to\infty} c_n > 1$ ならば絶対収束し，
$\displaystyle\color{red} \limsup_{n\to\infty} c_n <1$ ならば条件収束または発散する(正項級数 $a_n>0$ ならば発散する)。

この判定法は，根底に $\sum 1/n(\log n)^p$ の収束・発散と比較することで行われます。これは，1/nlogn型の級数の収束・発散より， $0<p\le 1$ のとき収束し， $p>1$ のとき発散することが分かっています。

かなり精度が良さそうですね。

【級数の収束判定法】Bertrand’s testの証明

早速証明しておきましょう。

証明

$a_n >0$ (正項級数)とし，その無限和が収束することを示せばよい。

$p = \liminf_{n\to\infty} c_n >1$ とする。また， $1< q_3<q_2<q_1<p$ となる $q_1,q_2,q_3$ を選ぶ(たとえば， $[1,p]$ の4等分点にすればよい)。

このとき，十分大きい $n$ について，

\frac{a_n}{a_{n+1}} \ge 1+\frac{1}{n} + \frac{q_1}{n\log n}

となる。さらに， $b_n = 1/n(\log n)^{q_3}$ とする。平均値の定理より，

\frac{1}{n+1} \le \log (n+1)-\log n=\log\frac{n+1}{n} \le \frac{1}{n}

であることと， $(1+x)^r$ のマクローリン展開を考えることで，十分大きな $n$ に対し，

\begin{aligned}\frac{a_n}{a_{n+1}} &\ge 1+\frac{1}{n} + \frac{q_1}{n\log n} \\ &= \frac{n+1}{n} \left(1+ \frac{q_1}{\log n}\frac{1}{n+1}\right) \\ &\ge \frac{n+1}{n} \left(1+ \frac{q_2}{\log n}\log \frac{n+1}{n}\right) \\ &\ge \frac{n+1}{n} \left( 1+ \frac{\log \frac{n+1}{n} }{\log n}\right)^{q_3} \\ & = \frac{b_n}{b_{n+1}} \end{aligned}

である。これを書き換えると， $a_{n+1}/b_{n+1}\le a_n/b_n$ であり， $\{a_n/b_n\}$ は十分大きい $n$ で広義単調減少である。特にこの数列は $K>0$ を用いて， $a_n/b_n\le K$ とかける。したがって，

a_n\le Kb_n

となる。1/nlogn型の級数の収束・発散から， $\sum_{n=1}^\infty b_n$ は収束するため， $\sum_{n=1}^\infty a_n$ も収束する。

証明終

不等式評価のところは，若干評価をサボった感がありますが，感覚的に分かってもらえるとよいと思います。

証明

$a_n>0$ (正項級数)とし，その無限和が発散することを示せばよい。

$x\log x$ に平均値の定理を適用することで，

(n+1)\log (n+1)-n\log n = 1+\log k_n

となる $n<k_n<n+1$ が存在することがわかる。 $b_n = 1/n\log n$ とすると，

\begin{aligned} \frac{b_n}{b_{n+1}}&=\frac{(n+1)\log(n+1)}{n\log n} \\ &= 1+\frac{\log k_n}{n\log n}+ \frac{1}{n\log n} \\ &\ge 1+\frac{1}{n} + \frac{1}{n\log n}.\end{aligned}

であるから，

\frac{a_n}{a_{n+1}}-\frac{b_n}{b_{n+1}} \le \frac{c_n-1}{n\log n}

となる。仮定より，十分大きな $n$ に対して，

\frac{a_n}{a_{n+1}}-\frac{b_n}{b_{n+1}} \le 0

が成り立つ。これを書き換えると， $b_{n+1}/a_{n+1}\le b_n/a_n$ であり， $\{b_n/a_n\}$ は十分大きい $n$ で広義単調減少である。特にこの数列は有界で， $K>0$ を用いて， $b_n/a_n\le K$ とかける。したがって，

b_n\le K a_n

であり，1/nlogn型の級数の収束・発散から， $\sum_{n=1}^\infty b_n$ は発散するため， $\sum_{n=1}^\infty a_n$ も発散する。

証明終

なお，証明より， $\limsup_{n\to\infty} c_n =1$ であっても，この収束が下から，すなわち「 $c_n\le 1$ かつ $\limsup_{n\to\infty} c_n =1$ 」であるなら，条件収束または発散することが分かります。

この収束判定を使う場面はそう多くないかもしれませんね。