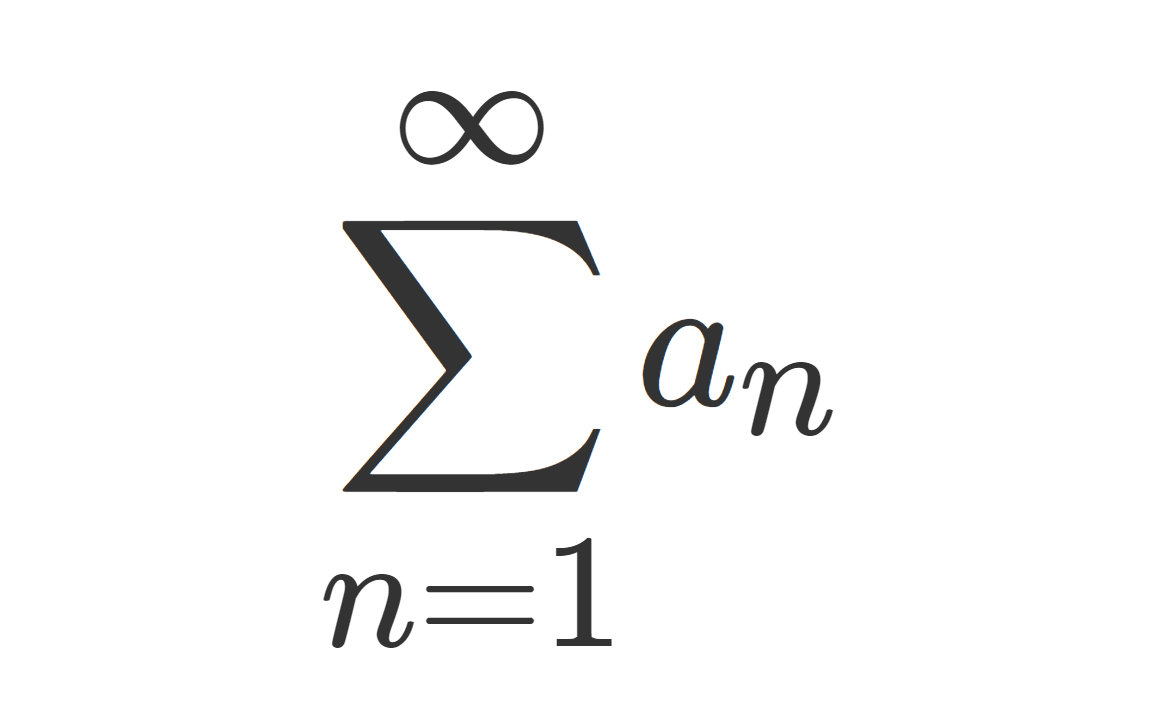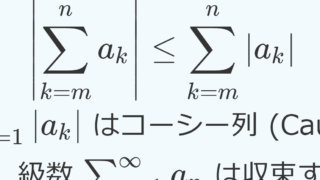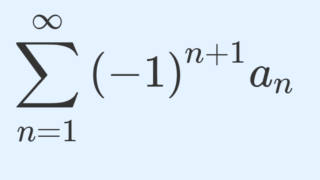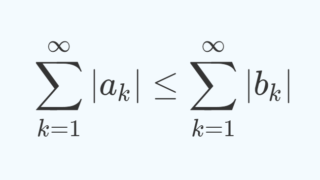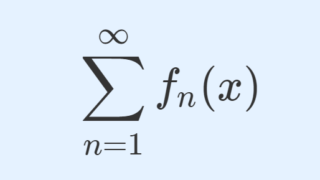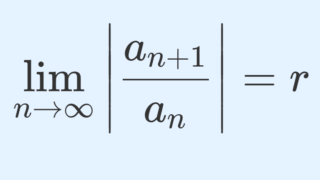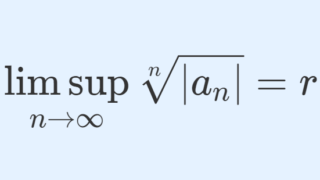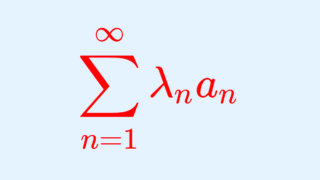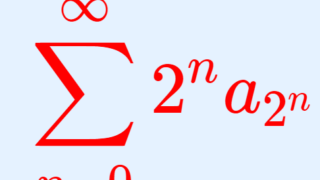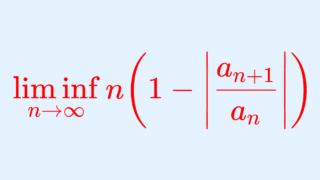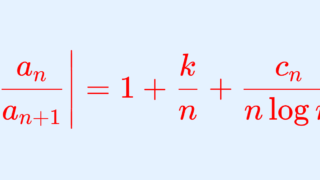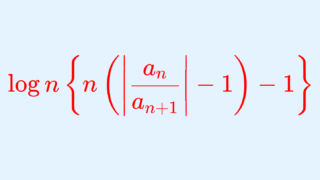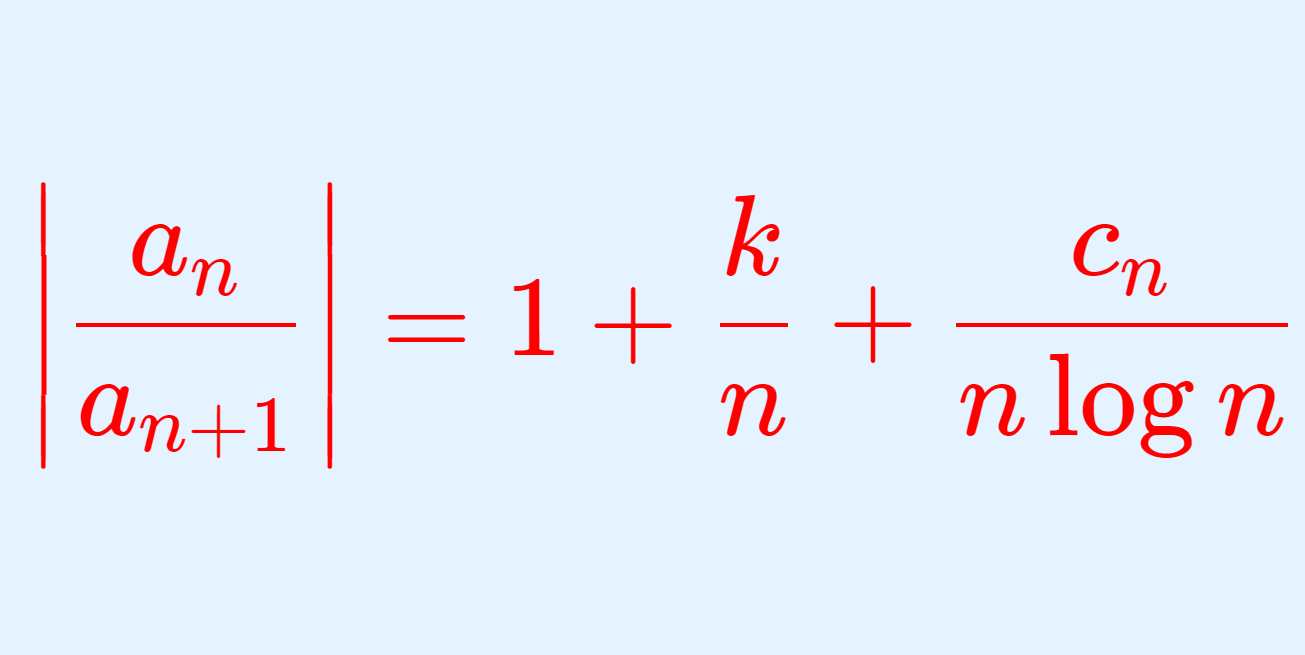級数 \displaystyle \sum_{n=1}^\infty a_n の収束判定法・発散判定法は,さまざまなものが知られています。これについて,有名な13個をまとめましょう。
【必須知識】級数の収束・発散判定法まとめ1
まず,理系大学生ならば理解しておくべき収束・発散判定法を列挙しましょう。使いやすい・判定しやすい順位列挙します。別の記事で解説しているものは,そのリンクを追記することにします。
各項が0に収束するかどうか
\sum_{n=1}^\infty a_n が収束すれば, \lim_{n\to\infty}a_n = 0 である。対偶を取ると, \lim_{n\to\infty}a_n \ne 0 ならば, \sum_{n=1}^\infty a_n は収束しない。
絶対収束すれば収束する
\sum_{n=1}^\infty |a_n|<\infty が成立するとき, \sum_{n=1}^\infty a_n も収束する。
交代級数の収束性(ライプニッツ)
\{a_n\} は a_n \ge 0 かつ広義単調減少, \lim_{n\to\infty} a_n = 0 とする。このとき,
\sum_{n=1}^\infty (-1)^{n+1} a_n
は収束する。
比較判定法
|a_n|\le |b_n| かつ \sum_{n=1}^\infty |b_n| < \infty ならば \sum_{n=1}^\infty |a_n| < \infty である。
なお,これを関数項級数に対して適用した以下の定理も有名です。
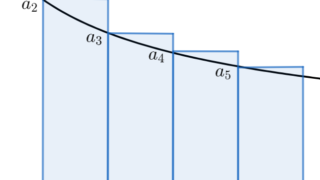
広義積分による収束判定法
a_n \ge 0 とする。もし f(n) = a_n となる広義単調減少な関数 f\colon [1,\infty) \to [0,\infty) が存在すれば, \sum_{n=1}^\infty a_n の収束・発散は広義積分 \int_1^\infty f(x)\,dx の収束・発散と一致する。
ダランベールの収束判定法
\displaystyle \lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| = r
が存在するとする。このとき, \sum_{n=1}^\infty a_n は 0\le r< 1 ならば絶対収束, r>1 ならば発散する。
コーシーの収束判定法
\displaystyle \limsup_{n\to\infty} \sqrt[n]{|a_n|} = r
とする。このとき, \sum_{n=1}^\infty a_n は 0\le r< 1 ならば絶対収束, r>1 ならば発散する。
前述したダランベールの判定法と,ここでのコーシーの判定法は,やりたいことは類似していますが,コーシーの判定法の方が適用範囲が広いことが知られています。
【知っておくとよい】 収束・発散判定法まとめ2
ここからは,「微分積分学で絶対に習うような必須知識」ではないですが,知っておくと役に立つこともある定理を紹介していきましょう。
アーベルの収束判定法
\{\lambda_n\} は有界かつ単調であるとし, \sum_{n=1}^\infty a_n は収束する(絶対収束または条件収束)とする。このとき,
\sum_{n=1}^\infty \lambda_n a_n
は収束する。
ディリクレの収束判定法
実数列 \{\lambda_n\} は単調かつ \lambda_n\xrightarrow{n\to\infty} 0 とし,数列 \{a_n\} はその部分和列 \{ \sum_{k=1}^n a_k\}_n が有界であるとする。このとき,
\sum_{n=1}^\infty \lambda_n a_n
は収束する(絶対収束または条件収束)。
Cauchy Condensation Test
\{a_n\} は a_n\ge 0 かつ広義単調減少とする。このとき, \sum_{n=1}^\infty a_n の収束・発散は
\sum_{n=0}^\infty 2^n a_{2^n}
の収束・発散に一致する。
ラーベの収束判定法
\sum_{n=1}^\infty a_n の収束・発散について,
\liminf_{n\to\infty} n\!\left(1-\left|\frac{a_{n+1}}{a_n}\right|\right) > 1\limsup_{n\to\infty} n\!\left(1-\left|\frac{a_{n+1}}{a_n}\right|\right) < 1
ならば絶対収束し,
ならば条件収束または発散する(正項級数 a_n>0 ならば発散する)。
ガウスの収束判定法
\sum_{n=1}^\infty a_n の収束・発散について,ある c_n\xrightarrow{n\to\infty}0 となる数列 \{c_n\} を用いて,
\left|\frac{a_n}{a_{n+1}}\right| = 1+\frac{k}{n} +\frac{c_n}{n\log n}
と表せるとする。このとき, k> 1 ならば絶対収束し, k\le 1 ならば条件収束または発散する(正項級数 a_n>0 ならば発散する)。
Bertrandの収束判定法
\sum_{n=1}^\infty a_n の収束・発散について,数列 \{c_n\} を用いて,
\left|\frac{a_n}{a_{n+1}}\right| = 1+\frac{1}{n} +\frac{c_n}{n\log n}c_n = \log n \left\{n\left( \left|\frac{a_n}{a_{n+1}}\right| - 1 \right) - 1\right\}
と表せるとする。すなわち,
である。このとき,\liminf_{n\to\infty} c_n > 1 ならば絶対収束し, \limsup_{n\to\infty} c_n <1 ならば条件収束または発散する(正項級数 a_n>0 ならば発散する)。