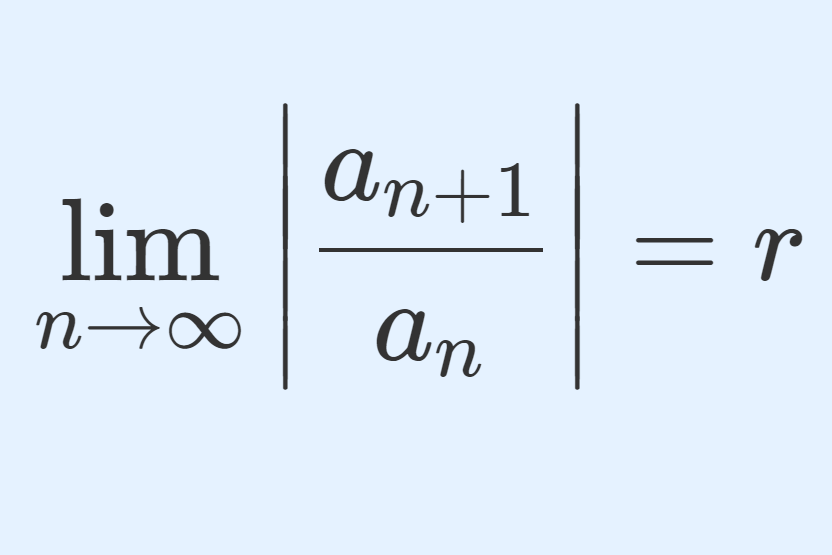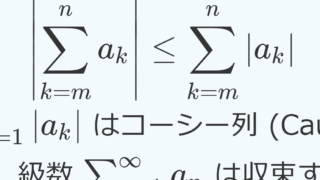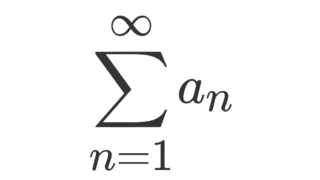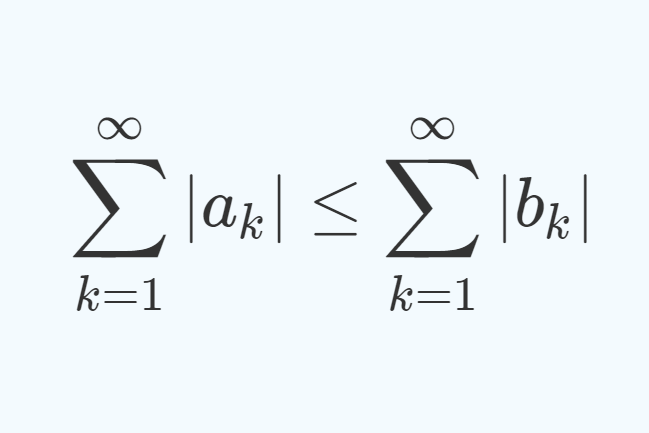級数の収束・発散を判定する方法(十分条件)として,最も有名なものの一つである,ダランベールの収束判定法について,その主張と具体例を紹介し,最後に証明を述べます。
ダランベールの収束判定法とその系
ダランベールの収束判定法
定理(ダランベールの収束判定法; d’Alembert’s ratio test)
数列 \{a_n\} に対し,
\lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| = rが存在するとする。このとき, \sum_{n=1}^\infty a_n の収束・発散について
- 0 \le r < 1 ならば絶対収束
- r > 1 ならば発散
となる。
r = 1 のときは,収束・発散の両方があり得ます。この例については後で取り上げます。
なお,あくまで十分条件であることに注意してください。これについても,後の具体例で,ダランベール判定法が使えないが収束・発散するものについて述べます。
絶対収束すなわち \sum_{n=1}^\infty |a_n| < \infty となるとき,元の級数 \sum_{n=1}^\infty a_n も有限値に収束することは有名です。これについては以下を参照してください。
ダランベールの収束判定法の直感的な理解
簡単のため, a_n \ge 0 (正項級数)としましょう。条件は a_{n+1}/a_n \xrightarrow{n\to\infty} r でしたが,
\frac{a_{n+1}}{a_n} = rと思うと,これは等比数列ですね。するとこれは,公比が 0 \ge r < 1 のとき収束して, r > 1 のとき発散すると言っているに過ぎません。
実際は等比数列ではありませんが,極限の意味で2項間の平均が r になるため,近似的に公比が r の等比数列といえます。近似的等比数列について収束・発散を判定しているのが,ダランベールの判定法なわけです。
ダランベールの収束判定法の系
ほぼ自明かもしれませんが,上の定理は以下のように拡張することができます。定理やその証明からすぐに従うの類似のものという意味で,「系」ということにしましょう。(→ 定義・公理・定理・命題・補題・系を完全理解しよう)
系
数列 \{a_n\} に対し, \sum_{n=1}^\infty a_n の収束・発散について
- \displaystyle \limsup_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| < 1 ならば絶対収束
- \displaystyle \liminf_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| > 1 ならば発散
となる。
ダランベールの収束判定法の具体例
の順に紹介しましょう。
なお,項の中に a_n = 0 となるものがあるような,ある意味「面白くない」例は扱いません。
ダランベールの判定法が適用できる例
絶対収束する例
例1.
\textcolor{red}{a_n = n/2^n} とすると,
\begin{aligned} \lim_{n\to\infty} \frac{(n+1)/2^{n+1}}{n/2^n} &= \lim_{n\to\infty} \frac{n+1}{2n} = \frac{1}{2} < 1 \end{aligned}より,ダランベールの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty \frac{n}{2^n} < \infty.}すなわち,絶対収束する。
例2.
\textcolor{red}{a_n = n!/n^n} とすると,
\begin{aligned} & \lim_{n\to\infty} \frac{(n+1)!/{(n+1)}^{n+1}}{n!/n^n} \\ &= \lim_{n\to\infty} \left(\frac{n}{n+1}\right)^n \\ &= \frac{1}{e} < 1 \end{aligned}より,ダランベールの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty \frac{n!}{n^n} < \infty.}すなわち,絶対収束する。
発散する例
例3.
\textcolor{red}{a_n = (-2)^{n+1} /\log (n+1) } とすると,
\begin{aligned} &\lim_{n\to\infty} \left|\frac{(-2)^{n+1}/\log (n+1)}{(-2)^n /\log n}\right| \\ &= \lim_{n\to\infty} \frac{2\log n}{\log (n+1)} \\ &= 2 > 1 \end{aligned}より,ダランベールの判定法が使えて,級数は発散する。
ダランベールの判定法は適用できないが系が適用できる例
収束する例
例4.
\textcolor{red}{a_n = 2^{-\lfloor 3n/2 \rfloor }} とする(ただし, \lfloor\cdot \rfloor は床関数(ガウス記号))。このとき,
\frac{2^{-\lfloor 3(n+1)/2 \rfloor}}{2^{-\lfloor 3n/2 \rfloor} }= \begin{cases} 1/4 & n = 2k-1, \\ 1/2 & n = 2k \end{cases}(ただし, k=1,2,3,\ldots )となるから, \lim_{n\to\infty} |a_{n+1}/a_n| は存在しないが,
\limsup_{n\to\infty} \left|\frac{a_{n+1}}{a_n} \right| = \frac{1}{2} < 1であるから,系が使えて
\textcolor{red}{\sum_{n=1}^\infty 2^{-\lfloor 3n/2 \rfloor} < \infty.}すなわち,絶対収束する。
発散する例
例5.
\textcolor{red}{a_n = 2^{\lfloor 3n/2 \rfloor }} とする(ただし, \lfloor\cdot \rfloor は床関数(ガウス記号))。このとき,
\frac{2^{\lfloor 3(n+1)/2 \rfloor}}{2^{\lfloor 3n/2 \rfloor} }= \begin{cases} 4 & n = 2k-1, \\ 2 & n = 2k \end{cases}(ただし, k=1,2,3,\ldots )となるから, \lim_{n\to\infty} |a_{n+1}/a_n| は存在しないが,
\liminf_{n\to\infty} \left|\frac{a_{n+1}}{a_n} \right| = 2 > 1であるから,系が使えて
\textcolor{red}{\sum_{n=1}^\infty 2^{\lfloor 3n/2 \rfloor} = \infty.}すなわち,発散する。
r = 1 となる例
絶対収束する例
例6.
\textcolor{red}{a_n = 1/n^2} とすると,
\lim_{n\to\infty}\frac{1/(n+1)^2}{1/n^2} = \lim_{n\to\infty} \left( \frac{n}{n+1} \right)^2 = 1であるから,ダランベールの判定法は使えないが,
\textcolor{red}{\sum_{n=1}^\infty \frac{1}{n^2} < \infty }となって絶対収束する。
条件収束する例
例7.
\textcolor{red}{a_n = (-1)^{n+1}/n} とすると,
\lim_{n\to\infty}\left|\frac{(-1)^{n+1}/(n+1)}{(-1)^n/n}\right| = \lim_{n\to\infty} \frac{n}{n+1} = 1であり,ダランベールの判定法は使えない。一方で,
\textcolor{red}{\sum_{n=1}^\infty \frac{1}{n} = \infty, \quad \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = \log 2.}すなわち,条件収束する。
発散する例
例8.
\textcolor{red}{a_n = 1/n} とすると,
\lim_{n\to\infty}\frac{1/(n+1)}{1/n} = \lim_{n\to\infty} \frac{n}{n+1} = 1であるから,ダランベールの判定法は使えず,
\textcolor{red}{\sum_{n=1}^\infty \frac{1}{n} = \infty }より収束しない。
ダランベールの判定法も系も適用できず,r = 1でもない例
絶対収束する例
例9.
\textcolor{red}{a_n = \begin{cases} 2^{-k} & n=2k-1, \\ 3^{-k} & n=2k \end{cases}, \, k=1,2,3,\ldots} とすると,
\limsup_{n\to\infty} \frac{a_{n+1}}{a_n} = \infty, \quad \liminf_{n\to\infty} \frac{a_{n+1}}{a_n} = 0より,ダランベールの判定法もその系も適用できないが, これは公比 1/2 の等比数列と公比 1/3 の等比数列を交互に足したものであるから, 絶対収束する。
条件収束する例
例10.
\textcolor{red}{a_n = \begin{cases} (-1)^{k+1}/k & n=2k-1, \\ (-1)^{k+1}/\sqrt{k} & n=2k \end{cases}, \, k=1,2,3,\ldots} とすると,
\limsup_{n\to\infty} \frac{a_{n+1}}{a_n} = \infty, \quad \liminf_{n\to\infty} \frac{a_{n+1}}{a_n} = 0より,ダランベールの判定法もその系も適用できないが,これは2つの条件収束級数を交互に足したものであるから,条件収束する。
2つの条件収束級数を交互に足したものが条件収束する理由は,
\begin{gathered}\sum_{j=1}^{2n} a_j = \sum_{k=1}^n a_{2k-1} + \sum_{k=1}^n a_{2k}, \\ \sum_{j=1}^{2n+1} a_j = \sum_{k=1}^{n+1} a_{2k-1} + \sum_{k=1}^n a_{2k} \\ \end{gathered}であることと, n\to\infty とすると右辺が収束することから従います。
発散する例
例11.
\textcolor{red}{a_n = \begin{cases} 2^{-k} & n=2k-1, \\ 1 & n=2k \end{cases}, \, k=1,2,3,\ldots} とすると,
\limsup_{n\to\infty} \frac{a_{n+1}}{a_n} = \infty, \quad \liminf_{n\to\infty} \frac{a_{n+1}}{a_n} = 0より,ダランベールの判定法もその系も適用できないが, これは a_n > 0, \, \limsup_{n\to\infty} a_n =1 より, \sum_{n=1}^\infty a_n =\infty となって発散する。
ここまで,さまざまな例を確認してきました。
ダランベールの収束判定法の証明
お待たせしました。最後に証明をしましょう。ダランベールの判定法とその系の両方に適用できる証明をします。
収束する方の証明
証明
\varepsilon > 0 を, r \le 1-2\varepsilon (あるいは \limsup_{n\to\infty} |a_{n+1}/a_n| \le 1-2\varepsilon )となるように取る。
条件より,ある N \ge 1 が存在して,
n \ge N \implies \left| \frac{a_{n+1}}{a_n}\right| \le 1-\varepsilonとできる。すなわち, |a_{n+1}| \le (1-\varepsilon) |a_n| \,\,(n\ge N) である。これより,
\begin{aligned} |a_{N+n}| &\le (1-\varepsilon) |a_{N+n-1}| \\ &\le \cdots \\ &\le (1-\varepsilon)^n |a_N| \end{aligned}であるから,
\begin{aligned} \sum_{k=1}^{N+n} |a_k| &= \sum_{k=1}^{N-1} |a_k|+ \sum_{k=0}^{n} |a_{N+k}| \\ &\le \sum_{k=1}^{N-1} |a_k|+ \sum_{k=0}^{n} (1-\varepsilon)^k |a_{N}| \\ &\le \sum_{k=1}^{N-1} |a_k| + \frac{1}{\varepsilon} |a_N| \end{aligned}であり,右辺は n によらないから,左辺で n\to\infty として, \sum_{k=1}^\infty |a_k| < \infty, すなわち絶対収束が分かった。
証明終
発散する方の証明
証明
\varepsilon > 0 を, r \ge 1+2\varepsilon (あるいは \liminf_{n\to\infty} |a_{n+1}/a_n| \ge 1+2\varepsilon )となるように取る。
条件より,ある N \ge 1 が存在して,
n \ge N \implies \left| \frac{a_{n+1}}{a_n}\right| \ge 1+\varepsilonとできる。すなわち, a_n \ne 0 かつ |a_{n+1}| \ge (1+\varepsilon) |a_n| \,\,(n\ge N) である。これより,
\begin{aligned} |a_{N+n}| &\ge (1+\varepsilon) |a_{N+n-1}| \\ &\ge \cdots \\ &\ge (1+\varepsilon)^n |a_N| \end{aligned}なので, \lim_{n\to\infty}|a_{n}| = \infty となる。特に, \lim_{n\to\infty} a_n \ne 0 なので, \sum_{n=1}^\infty a_n は収束しない。
証明終