微分積分学の基本定理とその証明

微分積分学の基本定理とは，リーマン和による積分と，原始関数の概念をつなげる重要かつ基本的な定理です。「微分と積分は逆の操作であることを保証する定理」と言ってもいいでしょう。これについて，その主張と証明を紹介します。

微分積分学の基本定理

微分積分学の基本定理 (Fundamental theorem of calculus)

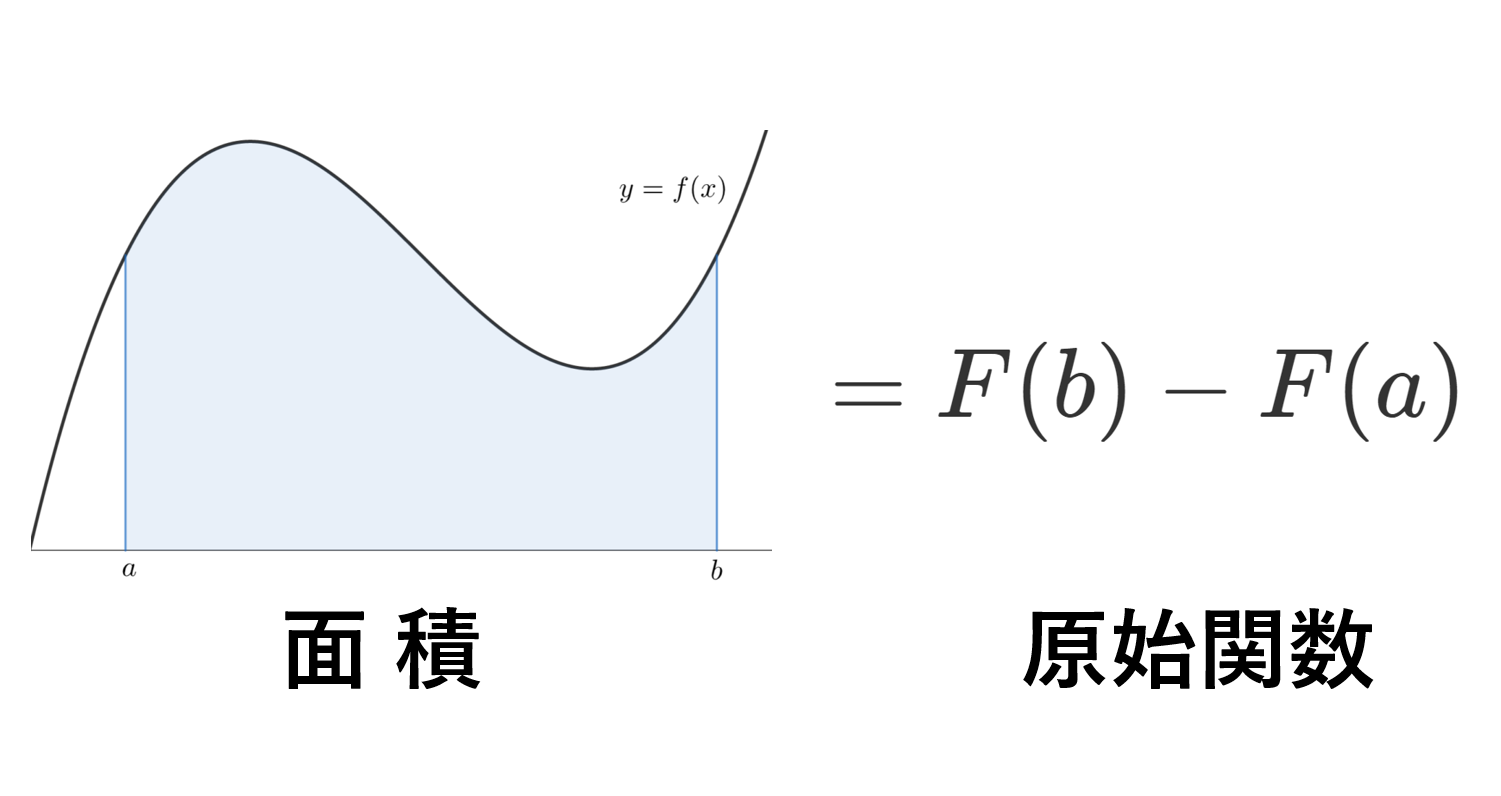
$f\colon [a,b]\to \mathbb{R}$ が(リーマン)積分可能かつ原始関数 $F$ を持つならば，

\color{red}\int_a^b f(x)\, dx = F(b)-F(a)

が成立する。

高校時代から当たり前に使っていた事実ですが，これは非常に重要です。（高校時代は若干導入の順序が変わるため，あまり意識していなかったと思います。）

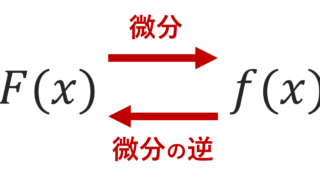
左辺はリーマン積分の定義から，「面積」(積分)を指します。一方で，右辺の原始関数 $F$ は「微分の逆」すなわち， $F'(x) = f(x)$ となるように定義されますから，面積は微分の逆で書けると言っているわけです。

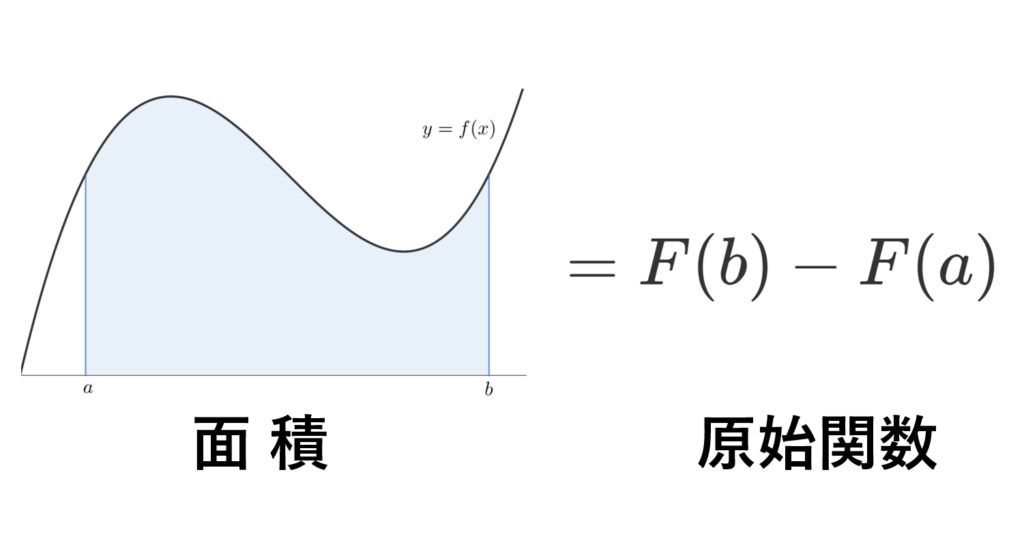
これを証明していきましょう。

証明

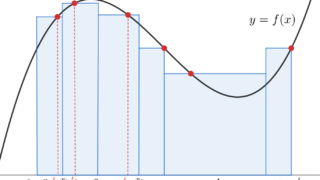
区間 $[a,b]$ を $n$ 等分割 ( $a=x_0 < x_1 < \dots < x_n =b$ ) する。平均値の定理より，各小区間で

F(x_k)-F(x_{k-1}) = f(t_k)(x_k-x_{k-1})

となる $x_{k-1} < t_k < x_k$ が存在する。よって，

\begin{aligned}F(b)-F(a) &= \sum_{k=1}^n (F( x_k)-F(x_{k-1})) \\ &= \sum_{k=1}^n f(t_k)(x_k-x_{k-1}). \end{aligned}

リーマン積分可能であることから，右辺は $n \to\infty$ で $\int_a^b f(x)\, dx$ に収束する。よって結論を得る。

証明終

平均値の定理さえ認めてしまえば，証明は非常にあっさりしたものでしたね。おつかれさまでした。