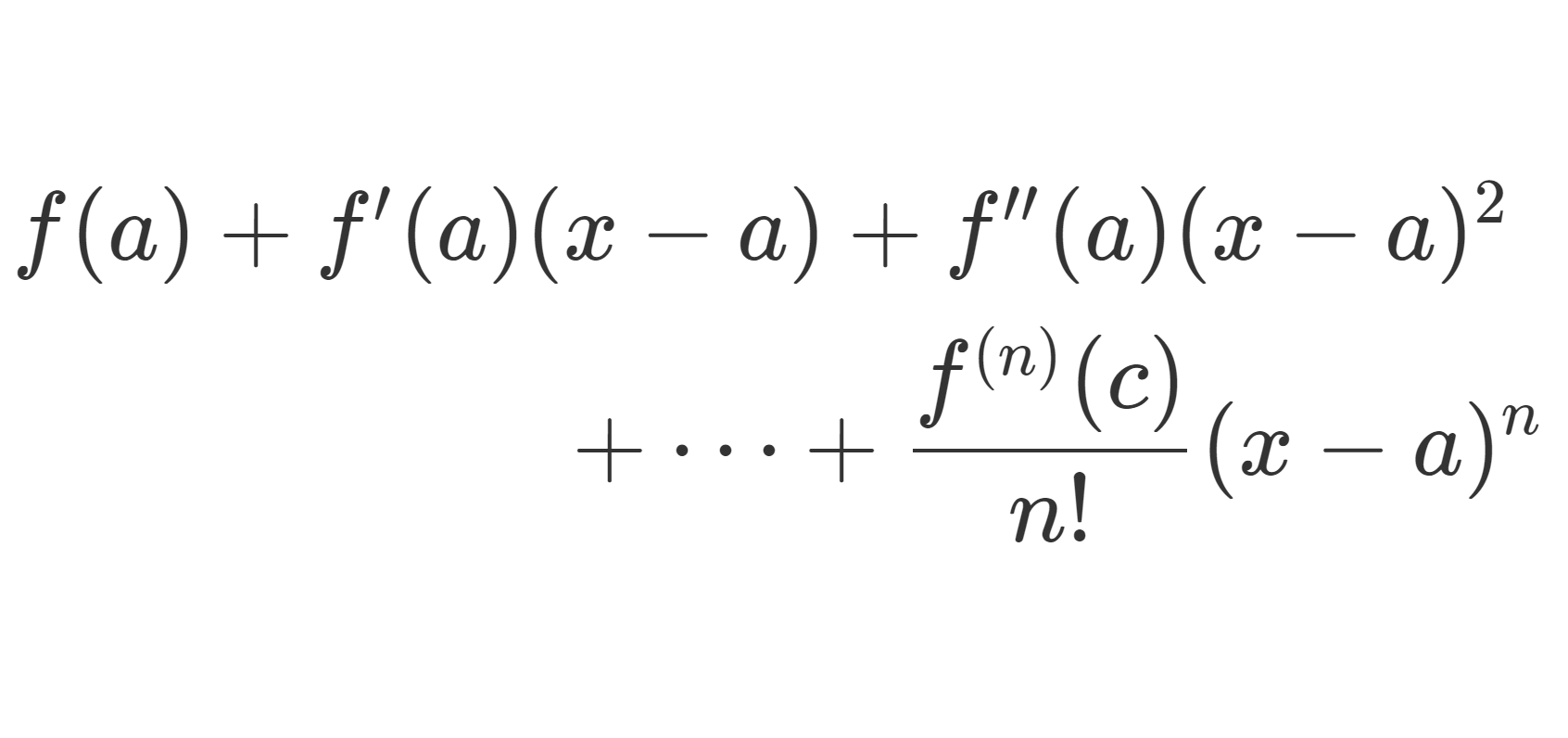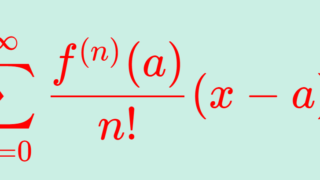平均値の定理の一般化であるテイラーの定理(テーラーの定理; Taylor’s theorem)とその特殊なものであるマクローリンの定理について,その主張と証明を紹介します。最後には,ラグランジュの剰余項の他にコーシーの剰余項など,さまざまな剰余項についても紹介します。
テイラー展開・マクローリン展開の基ともなるので,理解していきましょう。
テイラーの定理・マクローリンの定理
まずはテイラーの定理の主張を述べ,その特別な場合であるマクローリンの定理の主張も述べましょう。
テイラーの定理の主張
テイラーの定理 (Taylor’s theorem)
f は [a,x] 上 n-1 回連続微分可能(微分可能で f^{(n-1)} が連続)かつ (a,x) 上 n 回微分可能であるとする。このとき,
\small \color{red} \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k + \frac{f^{(n)}(c)}{n!}(x-a)^n \\ ={}& f(a)+ f'(a)(x-a) + \frac{f''(a)}{2}(x-a)^2 \\ &\hspace{50pt}+ \dots+ \frac{f^{(n)}(c)}{n!}(x-a)^n \end{aligned}
となる a<c<x が存在する。ここで,最終項 \color{red} R_n = \dfrac{f^{(n)}(c)}{n!}(x-a)^n をラグランジュの剰余項という。
いま,[a,x], (a,x) 上で考えましたが, [x,a], (x,a) 上で考えても構いません。 a の周りで考えるということが大切です。
この点で,テイラーの定理は f の a の周りでの n 階までの多項式展開ということができます。
マクローリンの定理の主張
テイラーの定理において, a = 0 とし, 0 の周りだけを考えているのがマクローリンの定理です。主張を述べましょう。
マクローリンの定理 (Maclaurin’s theorem)
f は [0,x] 上 n-1 回連続微分可能(微分可能で f^{(n-1)} が連続)かつ (0,x) 上 n 回微分可能であるとする。このとき,
\small\color{red} \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k + \frac{f^{(n)}(c)}{n!}x^n \\ ={}& f(0)+ f'(0)x + \frac{f''(0)}{2}x^2 \\ & \hspace{50pt} + \dots + \frac{f^{(n)}(c)}{n!}x^n \end{aligned}
となる 0<c<x が存在する。
マクローリンの定理は,コーシーの定理の特別な場合と言えます。すなわちマクローリンの定理は f の 0 の周りでの n 階までの多項式展開ということができます。
テイラーの定理・マクローリンの定理の証明
証明には「ロルの定理」を用います。これは,平均値の定理の証明の際にも用いたものです(→平均値の定理・ロルの定理とその証明)。
マクローリンの定理は,テイラーの定理で a = 0 としたものにすぎないため,テイラーの定理のみ証明しましょう。
証明
\small \begin{aligned}\varphi(y) ={}& \sum_{k=0}^{n-1} f^{(k)}(y) \frac{(x-y)^k}{k!} + R_n \cdot \frac{(x-y)^n}{(x-a)^n} \end{aligned}とおく。ただし,
\begin{aligned} R_n = f(x) -\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k \end{aligned}
と定める。このとき, \varphi(y) は [a,x] 上連続かつ (a,x) 上微分可能で, \varphi(a) = \varphi(x) = f(x) であることがわかる。よってロルの定理から, \varphi'(c) = 0 となる a<c<x が存在する。ここで,計算により
が分かるから,結局 R_n = \dfrac{f^{(n)}(c)}{n!}(x-a)^n となり,結論を得る。
証明終
さまざまな剰余項
ここまではラグランジュの剰余項を用いたテイラーの定理を紹介しましたが,他にもさまざまな剰余項があります。ここで代表的なものを紹介しましょう。以下,剰余項部分を
\color{red} \begin{aligned} R_n = f(x) -\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k \end{aligned}
と定義します。
ラグランジュの剰余項
a<c<x を用いて
\color{red} R_n = \dfrac{f^{(n)}(c)}{n!}(x-a)^n
となるようにしたもの,すなわち
としたものをラグランジュの剰余項 (Lagrange’s form of remainder) という。
また,これは 0<\theta<1 を用いて,
R_n = \dfrac{f^{(n)}((1-\theta)a+\theta x)}{n!}(x-a)^n
ともかけます。
コーシーの剰余項
a<c<x を用いて
\color{red} R_n = \dfrac{f^{(n)}(c)}{(n-1)!}(x-c)^{n-1}(x-a)
となるようにしたもの,すなわち
としたものをコーシーの剰余項 (Cauchy’s form of remainder) という。
また,これは 0<\theta<1 を用いて,
R_n = \dfrac{f^{(n)}((1-\theta)a+\theta x)}{(n-1)!}(1-\theta)^{n-1}(x-a)^{n}
ともかけます。これの証明は,
と定めてロルの定理を用いることで可能です。
ペアノの剰余項
f^{(n)}(y) は y =a で連続とする。このとき,
\color{red} R_n = \dfrac{f^{(n)}(a)}{n!}(x-a)^n + o(|x-a|^n)
(x\to a) と表現したもの,すなわち
としたものをペアノの剰余項 (Peano’s form of remainder) という。
ここで, o(|x-a|^n) \,\,(x\to a) はランダウの記号とよばれ, x\to a としたときに,比の意味で |x-a|^n よりも早く 0 に収束することを示します(→ランダウの記号とは~ビッグオー・スモールオー~)。
今回の場合は,ラグランジュの剰余項を用いると, o(|x-a|^n) は
\frac{f^{(n)}(c_x)-f^{(n)}(a)}{n!} (x-a)^n
に相当し, |x-a|^n で割ったものを x\to a とすると c_x \to a だから 0 に収束するので,確かにそうなっていますね。
剰余項の積分表現(ベルヌーイの剰余項)
f^{(n)}(y) は [a,x] 上で連続とする。このとき,
\color{red} R_n = \frac{1}{(n-1)!}\int_a^x(x-t)^{n-1} f^{(n)} (t) \, dt
と表現したもの,すなわち
としたものを剰余項の積分表現 (Integral form of remainder) という。
これは,部分積分により
\begin{aligned} R_{n-1} &= \frac{1}{(n-2)!}\int_a^x(x-t)^{n-2} f^{(n-1)} (t) \, dt \\ &= \frac{1}{(n-1)!}(x-a)^{n-1} (a) + R_n \end{aligned}
であることから,帰納法により分かります。
テイラーの定理・マクローリンの定理からテイラー展開・マクローリン展開へ
テイラーの定理・マクローリンの定理は,それぞれ n 次までの多項式近似でした。ここで, n\to\infty としたいと考えるのは,自然なことではないでしょうか。これがテイラー展開・マクローリン展開と呼ばれるものです。定義を述べましょう。
定義(テイラー展開・マクローリン展開)
f を C^\infty 級関数とする。 f が a の近くでのテイラーの定理の剰余項について R_n \xrightarrow{n\to\infty} 0 となるならば,
\small \color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(a)}{n!} (x-a)^n \\ &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2!} (x-a)^2 + \cdots \end{aligned}
とできる。これを f の a の周りのテイラー展開(テーラー展開; Taylor expansion) という。また, a= 0 としたときを特にマクローリン展開 (Maclaurin expansion) という。
この内容に詳細については,以下の記事で解説しています。