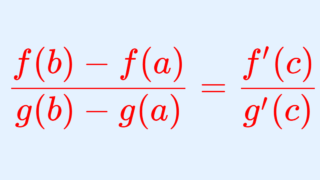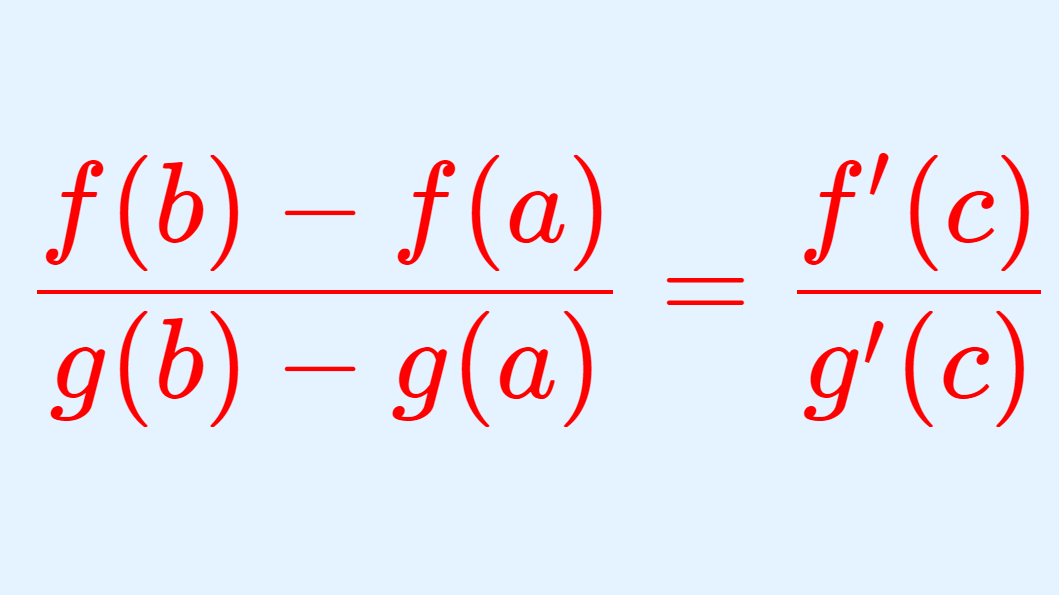高校理系数学や大学教養数学に登場する「平均値の定理」とその準備として「ロルの定理」を紹介し,その証明を行います。
平均値の定理・ロルの定理
まずは平均値の定理と,その準備となるロルの定理について,主張を確認していきましょう。
平均値の定理の主張
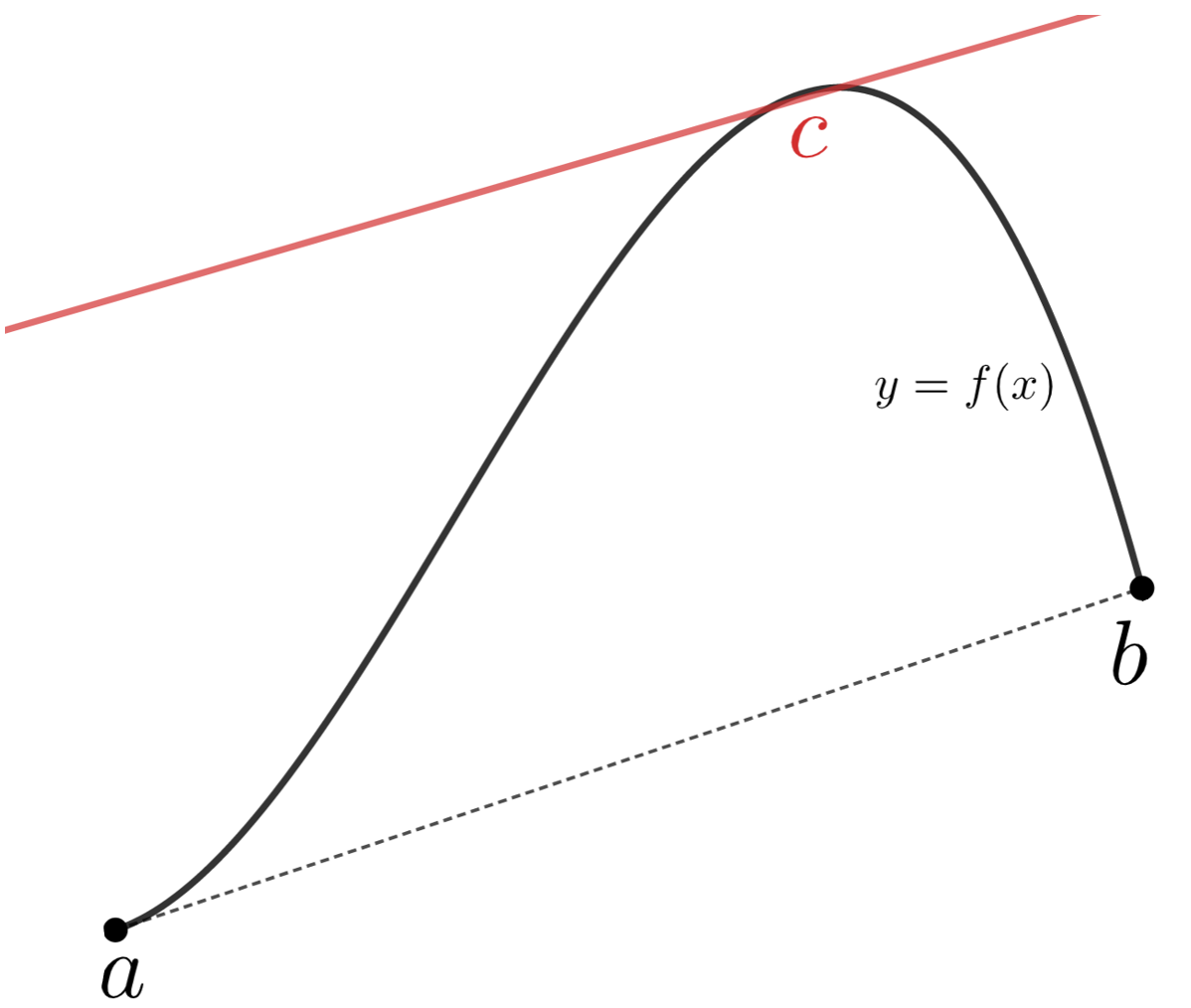
平均値の定理 (mean value theorem)
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき,
\color{red} \frac{f(b)-f(a)}{b-a} = f'(c) , \quad a < c< b
となる c が存在する。
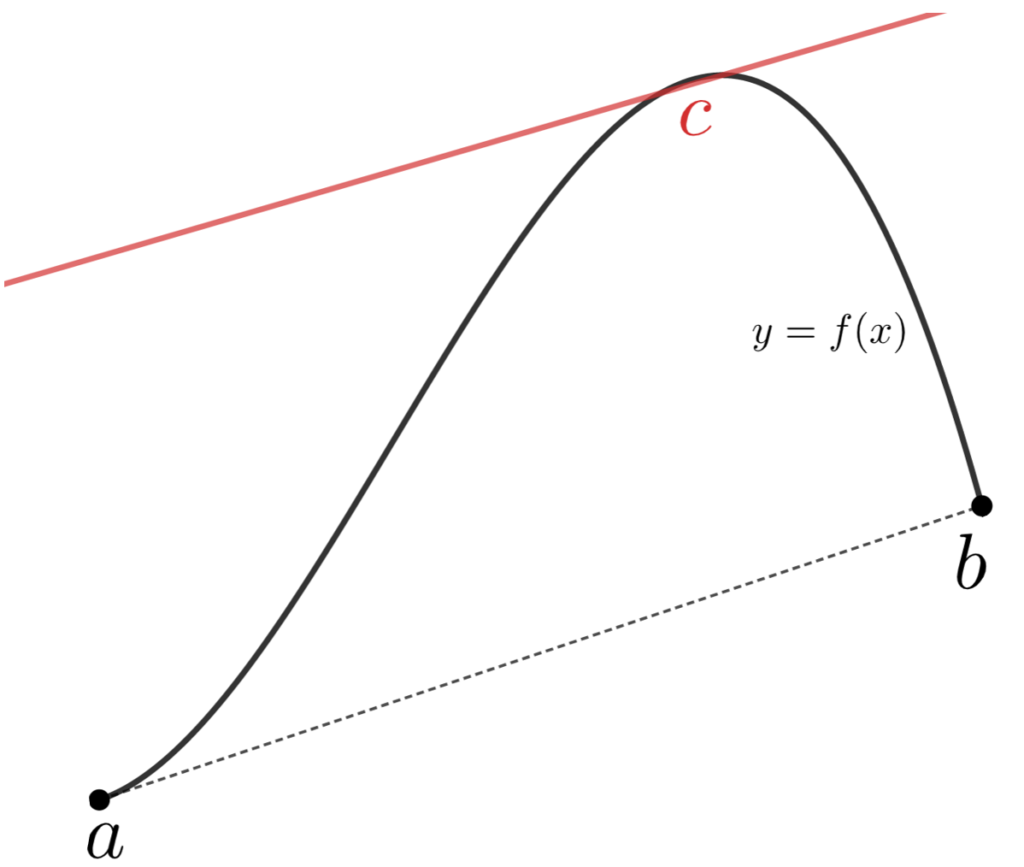
存在に関する定理です。点 (a,f(a)), (b,f(b)) 間の直線の傾きと同じ傾きの接線が取れると言っていますね。c の位置は関数によって変わります。
なお, c は [a,b] を \theta : (1-\theta) に内分する点と考え, c = (1-\theta)a+\theta b と書くことで,主張は以下のように書き直すことも可能です。
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき,
\color{red} \frac{f(b)-f(a)}{b-a} = f'((1-\theta)a+\theta b)
となる 0 < \theta < 1 が存在する。
平均値の定理の証明のためには,以下のロルの定理が使われます。
ロルの定理の主張
ロルの定理(Rolle’s theorem)
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき, f(a) = f(b) ならば,
\color{red} f'(c) = 0 , \quad a < c< b
となる c が存在する。
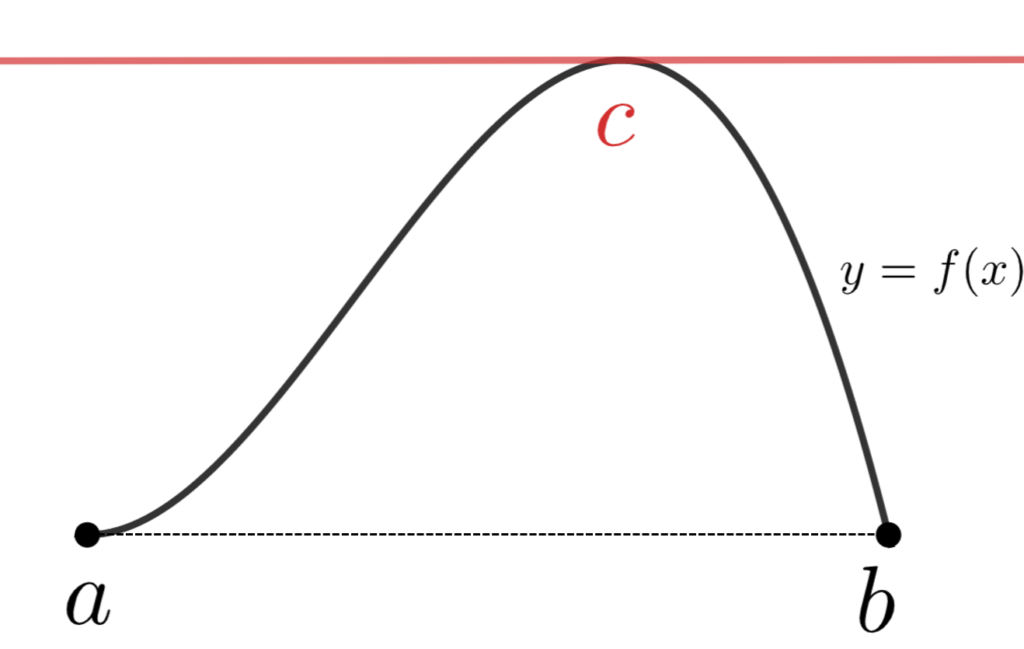
平均値の定理において, f(a) = f(b) としたものになっていますね。ロルの定理は,平均値の定理の特殊なバージョンと言えます。
平均値の定理・ロルの定理の証明
さて,順番に証明していきましょう。最大値・最小値定理を認めれば,高校生でも証明可能です。
ロルの定理の証明
証明
f は閉区間 [a,b] 上連続であるから,最大値・最小値定理により,最大値 M ・最小値 m をもつ(→【最大値定理】有界閉区間上の連続関数は最大値を持つことの証明)。
m=f(a) = f(b) = M のとき, f は定数関数なので明らか。よって m < f(a) = f(b) または f(a) = f(b) < M と思ってよい。どちらの証明も同様なので,後者のときに証明しよう。
このとき, f(c) = M となる a<c<b が取れる。
f(c-h) \le f(c) \,\, (a\le c-h \le c) なので, f の微分可能性より
が分かり, f(c) \ge f(c+h) \,\, (c \le c+h \le b ) なので,
もわかる。結果的に, f'(c) = 0 が従った。
証明終
ここで,極限による大小関係の保存 \psi_1(x) \le \psi_2(x), \,\, \alpha_1= \lim_{x\to a} \psi_1(x), \,\,\alpha_2 =\lim_{x\to a} \psi_2(x) \implies \alpha_1 \le \alpha_2 を認めましたが,これの証明は極限の性質6つの証明(一意性,和,積,商,大小関係)を参照してください。
平均値の定理の証明
さて,ロルの定理が証明できてしまえば,平均値の定理の証明はロルの定理に帰着させることで行うことができます。確認しましょう。
証明
\varphi(x) = f(x) - \left\{ \tfrac{f(b)-f(a)}{b-a}(x-a) + f(a) \right\}
とすると,これは [a,b] 上で連続, (a,b) 上で微分可能で, \varphi(a) = \varphi(b) = 0 であるから,ロルの定理が使えて, \varphi'(c) = 0 となる a<c<b が存在する。ここで,
であるから,結局
がわかる。
証明終
発展【コーシーの平均値の定理】
平均値の定理を拡張した,コーシーの平均値の定理というものもあります。最後にその主張を紹介しましょう。
コーシーの平均値の定理
関数 f,g は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき, g'(x) \ne 0 \,\,(a < x < b) ならば,
\color{red} \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)} , \quad a < c< b
となる c が存在する。
なお,これと比較して「普通の平均値の定理」をラグランジュの平均値の定理ということもあります。 g(x) = x とすれば,ラグランジュの平均値の定理になりますね。
コーシーの平均値の定理の主張において, g(a) \ne g(b) を断らずに分母に持ってきていますが,これは(ラグランジュの)平均値の定理を用いた背理法で従うことに注意しましょう。
実際,もし g(a) = g(b) とすると,(ラグランジュの)平均値の定理により, g'(c) = 0 となる c が存在せねばなりません。これは仮定に矛盾しています。
この定理については,以下の記事を参照してください。
その他の平均値の定理
平均値の定理のその他のバージョンについて,その主張を紹介しておきましょう。
積分の平均値の定理
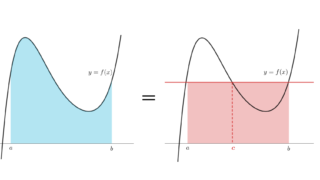
積分の平均値の定理
f は [a,b] 上連続かつ積分可能とする。このとき,
\color{red} f(c) = \frac{1}{b-a} \int_a^b f(x)\, dx
となる a<c<b が存在する。
積分バージョンの平均値の定理です。右辺が「積分の平均」になっていますね。これについては,以下の記事で解説しています。