最大値の定理・最小値の定理 (extreme value theorem) といわれる，連続関数における基本的な定理を紹介します。まず定理の主張を述べ，注意点を列挙してから，証明します。
最大値・最小値の定理の主張
定理（最大値・最小値の定理）
I \subset \mathbb{R} を(有界)閉区間とし， f\colon I \to \mathbb{R} を連続関数とする。
このとき， f は I 上で最大値と最小値をもつ。
ここで，「有界閉区間」とは， -\infty < a < b < \infty があって， I = [a, b] と表される区間のことを指します。
単に「閉区間」ということもありますが，位相空間論(という分野)における閉集合の定義では，\mathbb{R} 上 \mathbb{R} = (-\infty, \infty) は閉区間とも言えますので，「有界」という言葉を付けています。（有界性に関しては，有界とは何か～有界数列(点列)・有界関数・有界集合(区間)～も確認してください。）
ここでのポイントは以下の3つです。その「ポイント」が成り立たないときの反例も含めて，確認していきましょう。
- 閉区間であること
→ もし I = (0,1)（開区間）とし， f(x) = x とすると， f は最大値・最小値を持たなくなってしまう。
- 連続関数であること
→ もし I = [0, 1] とし， f(x) = \begin{cases} 1/x &x \in (0, 1], \\ 0 & x = 0 \end{cases} （連続でない）と定めると，これは最大値を持たなくなってしまう。
- 閉区間は有界であること
→ もし， I = (-\infty, \infty) とする(これも広義の閉区間！)と， f(x) =x はこの上で最大値・最小値を持たなくなってしまう。
「有界閉区間」上の「連続」関数であることが重要なことが分かったと思います。
最大値の定理の証明
「有界閉区間」，「連続」がどこで使われているか確認しながら読み進めていきましょう。
証明
最大値が存在することのみを証明すれば， -f を考えることで最小値の存在にも適用できるため，最大値のみ考える。
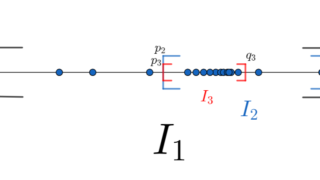
M = \sup_{x\in I} f(x) \in (-\infty, \infty] とおく(supは上限)。このとき，ある点列 \{a_n\} \subset I が存在して， f(a_n) \to M \,\, (n\to\infty) となる。
一方で， I は有界であったから，ボルツァノ－ワイエルシュトラス (Bolzano－Weierstrass) の定理により， \{a_n\} は収束部分列 \{a_{n_k}\} をもつ。特に， I は閉なので， a_{n_k} \to a \in I \,\, (n\to \infty) である。
f は連続であるため，上記のことから， f(a_{n_k}) \to f(a) となる。よって， f(a) = M であり，特に M < \infty でもあり， f は x = a \in I で最大値を持つ。
証明終
ボルツァノ－ワイエルシュトラスの定理が鍵になりました。
ボルツァノ－ワイエルシュトラスの定理については以下の記事を参照してください。
多次元の場合の最大値の定理
\mathbb{R}^n 上の関数についても，まったく同様の証明で以下が成立します。
定理（最大値・最小値の定理；多次元版）
D \subset \mathbb{R}^n を有界閉領域とし， f\colon D \to \mathbb{R} を連続関数とする。
このとき， f は D 上で最大値と最小値をもつ。
最大値・最小値の定理に関する補足
連続関数 f は， a\le x \le b 上最大値をもつことが分かったので， \max_{a\le x\le b} f(x) が意味を持ち，
\textcolor{red}{ \max_{a\le x\le b} f(x) = \sup_{a\le x\le b} f(x)}
が成立します。教科書などで，右辺でなく左辺のように書かれたときは，この定理を使っており，読み手に「最大値の定理くらい知ってるよね」と暗に主張しているのです。
こういったことはよくありますから，この定理は忘れないようにしましょう。
