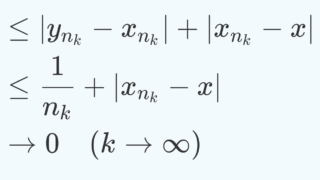中間値の定理とは，連続関数なら，間の値を全て取るという一見当たり前の定理です。これについて，その主張と，その証明を紹介します。さらに，根底にある「当たり前の性質」が何なのかも考えましょう。
中間値の定理とその証明
まずは，中間値の定理の主張とその証明を確認しましょう。
中間値の定理
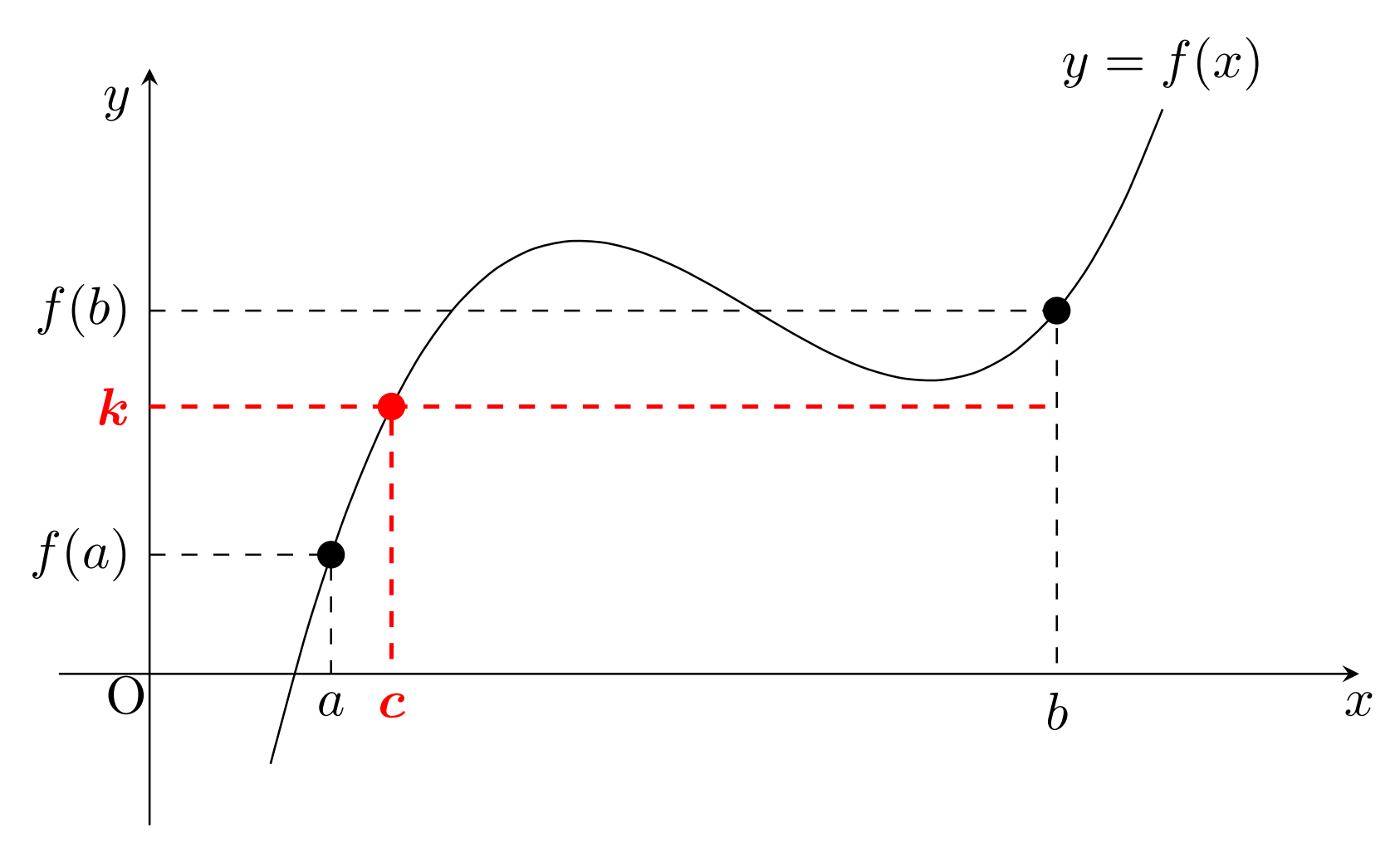
定理（中間値の定理; intermediate value theorem）
f\colon [a, b] \to \mathbb{R} を連続関数とする。
このとき， f は f(a) と f(b) の間の値を全てとる。
すなわち， f(a) < f(b) とすると，任意の f(a) < k < f(b) に対して， f(c) = k となる a < c < b が少なくとも一つ存在する。
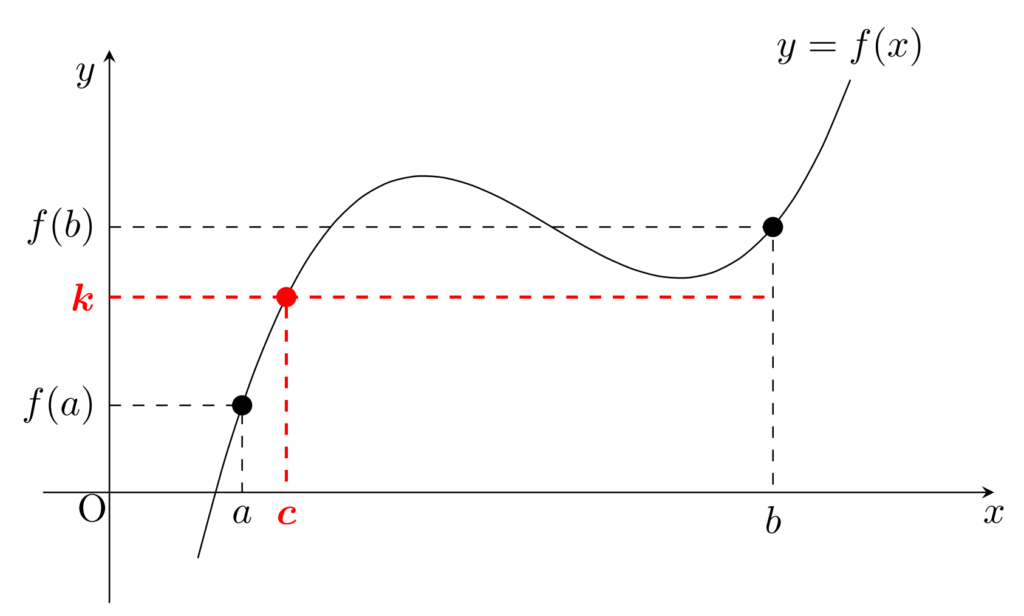
「存在性」の定理のため， c がどこにあるのかはわかりません。
連続関数は「つながっている」わけですから，間の値を全部取ることくらい，当たり前に思えるかもしれませんが，これには実数の連続性が深く関係しています。
中間値の定理の使用例
証明を述べる前に，中間値の定理の基本的な使用例を挙げましょう。
中間値の定理の使用例
f(x) = \sin x + x - e^{-x} とすると， f(x) = 0 は区間 (0, \pi/2) の間で実数解をもつ。
実際， f(0) = -1, f(\pi/2) = 1+ \pi/2 - e^{-\pi/2} から， f(0) < 0 < f(\pi/2) なので，中間値の定理より (0, \pi/2) の間で解をもつ。
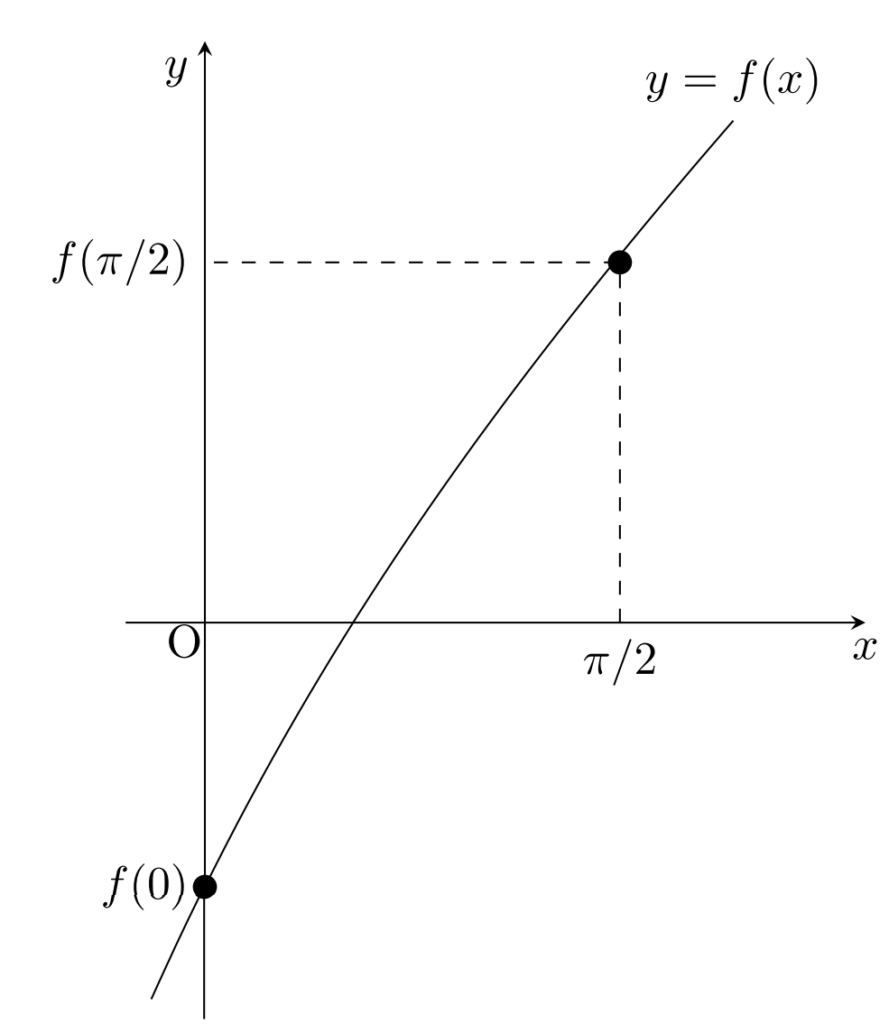
方程式の解の存在に適用するのは，最も基本的な適用方法だといえるでしょう。
それでは，証明にうつります。
中間値の定理の証明
証明
後半を示す。 c = \sup \{ x \in [a,b] \mid f(x) \le k \} とおく。 f(c) = k となることを示そう。
\sup の性質より， f(x_n) \le k, \,\, x_n \xrightarrow{n\to\infty}c となる \{x_n\} が存在する(→上限,下限(sup,inf)の定義と最大,最小(max,min)との違い)。
これと f の連続性より， f(x_n) \xrightarrow{n\to\infty} f(c) なので， f(c) \le k となる。
一方で， c < x^\prime_n, \,\, x^\prime_n \xrightarrow{n\to\infty} c となる \{x^\prime_n\} をとる（たとえば x^\prime_n = c + (c-b) / n とすればよい）。
すると， f(x^\prime_n) > k, \,\, f(x^\prime_n) \xrightarrow{n\to\infty} f(c) であるため， f(c) \ge k である。
以上から f(c) = k となるため，証明が終わる。
証明終
最初における \sup 値の存在の部分で，実数の連続性を使っています(→デデキント切断による実数の構成を解説)。
中間値の定理の本質と成り立たない場合
実数の連続性がポイントだといいました。実際，「連続性」がないと，以下のような反例が成立します。
「連続性」がない場合の反例
f\colon \textcolor{red}{[0, 1] \cap \mathbb{Q}} \to \mathbb{R} を， f(x) = x と定めると， これは [0, 1] \cap \mathbb{Q} 上連続関数であるが，中間値の定理は成立しない。
実際， f(0) = 0 < 1/\sqrt{2} < 1 = f(1) に対し， f(x) = 1/\sqrt{2} となる x \in [0, 1] \cap \mathbb{Q} は存在しないため，中間値の定理が成り立たないのが分かります。
これは，有理数が「連続性」を持たないことに起因します。
この「連続性」は位相空間論により一般化されます。最後に，位相空間論の言葉を用いた定理の主張を述べましょう。
位相空間論における中間値の定理
定理（中間値の定理; intermediate value theorem; 位相空間論ver.）
X を連結とし，f\colon X \to \mathbb{R} を連続とする。
a, b\in X を固定するとき， f は f(a), f(b) の間の値を全てとる。
ここで本質となるのは以下の定理です。
定理（連結性の保存）
X, Y を位相空間とし， f\colon X \to Y を連続とする。
このとき， A \subset X を連結とすると， f(A) \subset Y も連結となる。
「連結性」がキーを握っているわけですね。
証明はたとえば参考文献の定理 25.1,25.4 を参照してください。
おわりに
中間値の定理は，一見当たり前のように思えるかもしれませんが「実数の連続性」，位相空間論の言葉では「連結性」が大切だということです。
なお，有界閉区間上の連続関数は他にもさまざまな良い性質が成立します。たとえば，以下の記事を参照してください。
