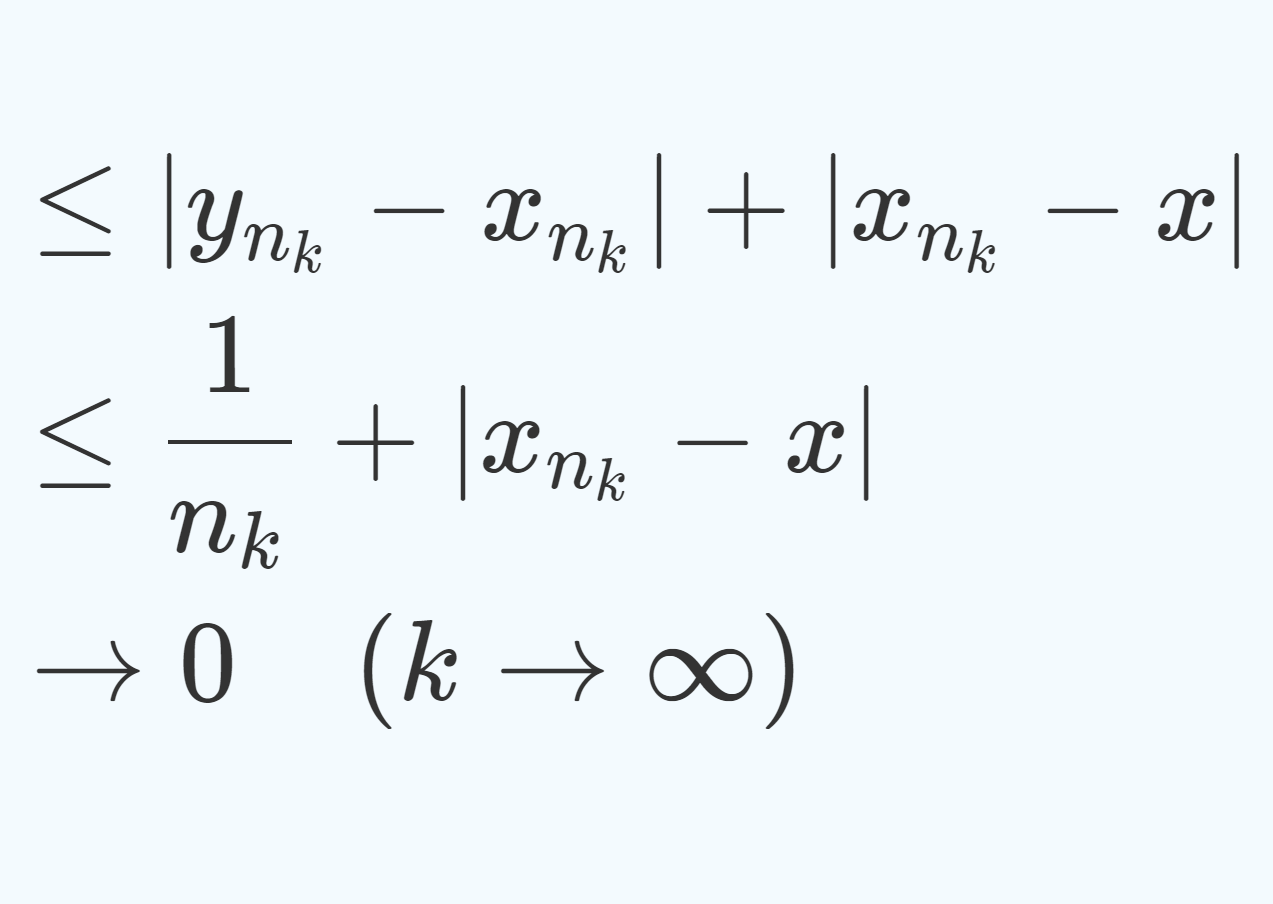一様連続性は連続性より強い概念ですが，有界閉区間上であれば，連続性だけで一様連続が従います。この定理を証明していきましょう。
「一様連続」と「連続」の違いは以下を参考にしてください。
有界閉区間上連続 ⇒ 一様連続
まずは今回証明する定理の主張を述べましょう。
定理（有界閉区間上連続ならば一様連続）
I を有界閉区間， f\colon I \to \mathbb{R} を連続関数とする。このとき， f は一様連続である。
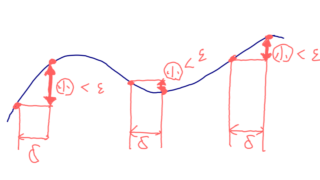
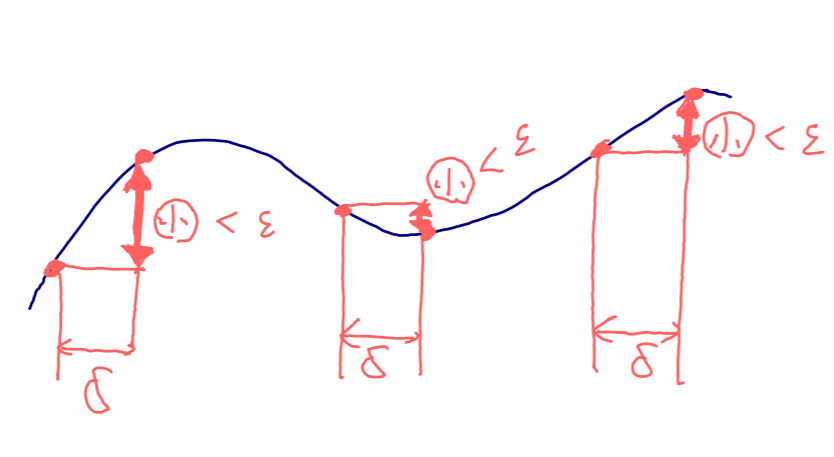
すなわち，任意の \varepsilon > 0 に対して，ある \delta > 0 が存在して，
|x-y|<\delta \Longrightarrow |f(x) - f(y)| < \varepsilon
が成立する。
一様連続性は数学において，便利な性質の一つです。そのため，連続から一様連続が従うのはとても嬉しいことです。
早速証明に移りましょう。
有界閉区間上連続 ⇒ 一様連続の証明
証明
背理法で示そう。もし一様連続でないと仮定すると，
ある \varepsilon > 0 が存在して， 各 n \ge 1 に対し，ある x_n, y_n \in I が存在して， |x_n - y_n| < 1/n かつ |f(x_n) - f(y_n) | \ge \varepsilon とできる。
\{x_n\} \in I は有界列であるから，ボルツァノ－ワイエルシュトラス (Bolzano–Weierstrass) の定理より， 収束部分列 \{ x_{n_k}\} が存在する。 I は閉であるから， x_{n_k} \to x \in I となる。またこのとき，
\begin{aligned} |y_{n_k} - x | &\le |y_{n_k} - x_{n_k}| + |x_{n_k} - x| \\ &\le \frac{1}{n_k} + |x_{n_k} - x| \\ &\to 0 \quad (k \to \infty) \end{aligned}
であるから， y_{n_k} \to x でもある。
f の連続性より，
\begin{aligned} \varepsilon &\le |f(x_{n_k}) - f(y_{n_k})| \\ &\to |f(x) - f(x) | \quad (k\to\infty) \\ &=0 \end{aligned}
となるが，両辺を確認すると，これは矛盾している。
よって結論が示せた。
証明終
証明の最初，「～とできる」のところを理解するのが最も難しいのではないかと思います。
主張の否定の取り方は，「任意の」と「ある，存在する」を入れ替えて，「AならばB」を「AであってBでない」にすればよいです。
本定理は専門数学をやる上で重要ですから，しっかり覚えておくようにしましょう。
