大学教養数学のさまざまなところに登場する,ボルツァノ–ワイエルシュトラスの定理についてその主張と証明を紹介します。
ボルツァノ–ワイエルシュトラスの定理
証明には,「実数の連続性」が深く関係しています。早速証明していきましょう。
証明
\{a_n\} \subset I_1, \,I_1= [p_1, q_1] とする。区間 [p_1, (p_1+q_1)/2], [(p_1+q_1)/2, q_1] のうち,少なくとも一方は \{a_n\} の項のうち無限個を含む。すなわち,
\begin{gathered} \#\{n\mid a_n \in [p_1, (p_1+q_1)/2]\} = \infty \\ \text{or}\\ \#\{n \mid a_n \in [(p_1+q_1)/2, q_1] = \infty \end{gathered}である。このうち,無限となる方の区間を I_2 = [p_2, q_2] とおく。(どちらも無限になる場合はどちらでもよい。)
次に, I_2 を再び中点で分け, \{a_n\} の項のうち無限個を含む方を一つ取り,それを I_3 = [p_3, q_3] とする。
同様の操作により,閉区間の列 I_n = [p_n, q_n] を作る。(下の図を参照)
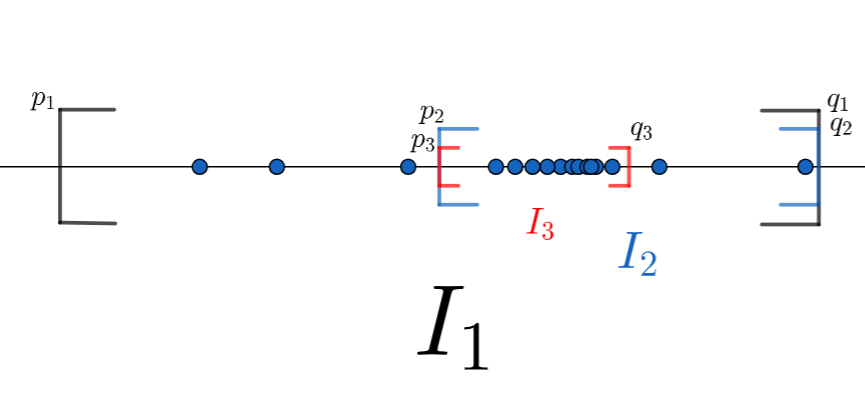
I_1 \supset I_2 \supset I_3 \supset \cdots より,
p_1 \le p_2 \le \cdots \le p_n \cdots \le q_n \le \cdots \le q_2 \le q_1であり,特に \{p_n\},\{q_n\} はそれぞれ有界な単調増加,単調減少列なので,収束値を持つ。それを p = \lim_{n\to\infty}p_n, q = \lim_{n\to\infty} q_n と定めよう。
いま,区間の取り方により, q_n - p_n = (q_{n-1} - p_{n-1})/2 = \cdots = (q_1 - p_1) / 2^{n-1} であるから, q_n - p_n \to 0 \, (n\to\infty) なので, q - p = 0 ,すなわち p = q である。
ここで, a_{n_1} \in I_1 を適当にとる。 I_2 は無限個の項を含むから, a_{n_2} \in I_2 , n_2 > n_1 となる n_2 がとれる。同様の操作により, a_{n_k} \in I_k を n_1 < n_2 < \cdots < n_k < \cdots となるように取る。
このとき, p_k \le a_{n_k} \le q_k で, p_k, q_k \xrightarrow{k\to\infty} p(=q) であったから, a_{n_k} \xrightarrow{k\to\infty}p(=q) であり,特に \{a_{n_k} \} は収束部分列になっている。
証明終
証明の途中,「それぞれ有界な単調増加,単調減少列なので,収束値を持つ」の部分で実数の連続性を利用しています。
多次元の場合のボルツァノ–ワイエルシュトラスの定理
\mathbb{R}^n の場合でも同様のことが成り立ちます。
略証をしておきます。
略証
まず \mathbb{R}^n の第1成分に対して収束部分列をとり,その部分列に関して,第2成分が収束するよう,さらに収束部分列をとり,という操作を繰り返せばよい。
略証終
位相空間論の言葉を用いた定理の主張
最後に,より高度な用語を用いた定理の主張を記しておきます。
定理(ボルツァノ–ワイエルシュトラス;Bolzano–Weierstrass; 位相空間論版)
I \subset \mathbb{R} を有界閉区間とするとき,これはコンパクトである。
より一般に, D \subset \mathbb{R}^n を有界閉集合とするとき,これはコンパクトである。
\mathbb{R}^n の位相(より一般に距離空間の位相)においては,点列コンパクト性とコンパクト性が同値になることを用いています。
大事な注意ですが,一般の距離空間においては,有界閉集合であってもコンパクトであるとは言えません。距離空間においては,「全有界」かつ「完備」であることがコンパクトであることの必要十分条件になります。
逆について
ここまで「有界 \implies 収束部分列が存在」を証明してきました。逆については,常に「収束列 \implies 有界」が成立します。これは,以下で解説しています。