収束する数列は有界であることを証明します。数列の極限を厳密に定義する \varepsilon \text{-} N 論法の演習の一つとしても最適なので,しっかり確認しましょう。
定理の主張~収束⇒有界~
定理(収束する数列は有界)
\{a_n\} を収束する数列とする。このとき,この数列は有界である。
証明する前に「収束する」の定義,「有界である」の定義を復習しておきます。
収束・有界の定義の復習
定義(数列の収束)
\{a_n\} を数列とする。 \{a_n\} が \alpha に収束する (converge) とは,
任意の \varepsilon > 0 に対して,ある N \ge 1 が存在して,
n \ge N \implies |a_n - \alpha | < \varepsilon
となることである。
イプシロンエヌ論法ですね。これについては,以下の記事で長文にわたって詳しく解説しています。
定義(数列の有界性)
\{a_n\} を数列とする。 \{a_n\} が有界である (bounded) とは,
ある K > 0 が存在して,
|a_n| \le K, \quad (n \ge 1 )
となることである。
各 n \ge 1 によらずに,大きさが定数 K で抑えられるということですね。これについては,以下でも解説しています。
定理の証明
さて,定理を証明していきましょう。
証明
\lim_{n\to\infty} a_n = \alpha とする。 \varepsilon > 0 を一つ定めると,収束の定義から,ある N \ge 1 が存在して,
n \ge N \implies |a_n - \alpha | < \varepsilon
となる。ここで,
と定めると,
であり,有界である。
証明終
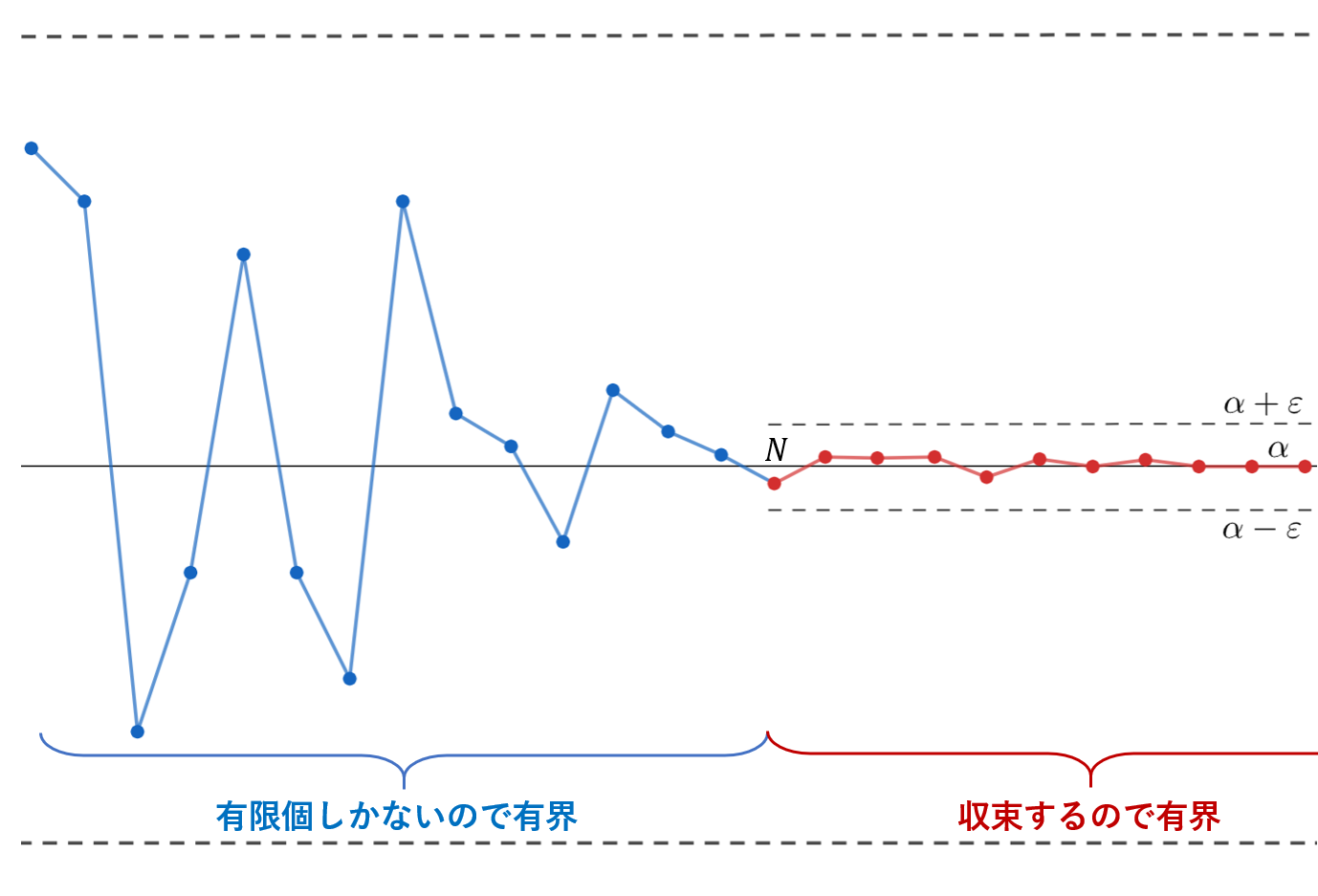
証明は短いかもしれません。図で表現すると,以下のような理屈です。
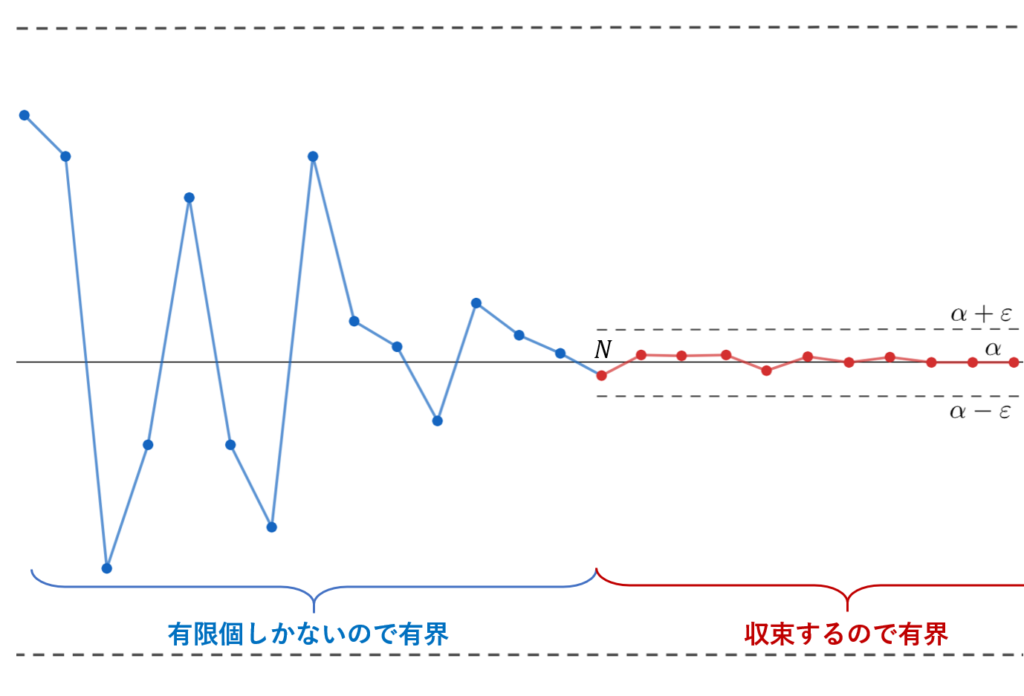
この定理は周知の事実ですから,しっかりと覚えておきましょう。
逆は成り立たないが,収束部分列は存在する
ここまで,「収束 \implies 有界」を証明しましたが, 一般に逆,すなわち「有界 \implies 収束」は成立しません。
ですが,部分列であれば, 収束するものが存在することが知られています。これを,ボルツァノ-ワイエルシュトラスの定理 (Bolzano- Weierstrass Theorem) と言います。これの証明は,以下の記事で解説しています。
「収束の基本的なこと」に関する他の話題
- イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~
- イプシロンデルタ論法をわかりやすく丁寧に~関数の極限の定義~
- 極限の性質6つの証明(一意性,和,積,商,大小関係)
- はさみうちの原理とその厳密な証明~数列版・関数版~
- 追い出しの原理とその厳密な証明~数列版・関数版~
- 上に有界な単調増加数列は収束することの証明
- 実数上関数の収束と数列の収束の同値性とその証明
- 【微分積分学】コーシー列とは~定義と収束性の証明~
- 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明