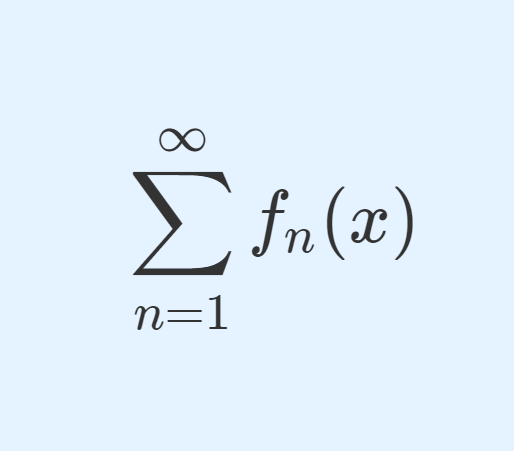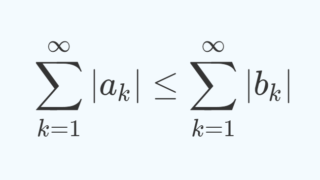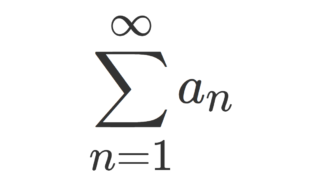ワイエルシュトラスのM判定法(優級数定理)とは～証明と具体例～

関数項級数の一様収束を判定する最も基本的な方法である，ワイエルシュトラスのM判定法（優級数定理ともいう）について紹介し，証明・例示します。

一様収束については，以下の記事を参照してください。

ワイエルシュトラスのM判定法

定理（ワイエルシュトラスのM判定法; Weierstrass M-test）

集合 $A$ 上の実数値または複素数値の関数列 $\{f_n\}$ に対し，ある数列 $\{M_n\}$ が存在して， $|f_n(x)| \le M_n \,\,(x \in I)$ かつ $\sum_{n=1}^\infty M_n < \infty$ ならば，

\sum_{n=1}^\infty f_n(x)

は $I$ 上絶対一様収束（絶対収束かつ一様収束）する

$x \in A$ によらず，常に $|f_n(x)| \le M_n$ と上から抑えられることがポイントです。

なお，集合 $A$ は有界でなくても構いません。任意の $x \in I$ について $|f_n(x)| \le M_n$ が成り立つようなものであれば何でもよいです。

ワイエルシュトラスのM判定法は，級数の収束を議論する，比較判定法の関数項バージョンだといえるでしょう。比較判定法については，以下の記事を参照してください。

定理の証明を簡単に行っておきましょう。

証明

以下では， $x \in A$ とする。

\sum_{k=m}^n |f_k(x)| \le \sum_{k=m}^n M_k

と， $x$ に依らないもので評価でき，コーシー列の性質より

\sum_{k=m}^n M_k \xrightarrow{m,n \to\infty} 0

であるから， $\{\sum_{k=1}^n |f_k(x)| \}_n$ は一様コーシー列である。よってこれは一様収束する。すなわち， $\sum_{k=1}^\infty f_k(x)$ は絶対一様収束する。

証明終

例1.

$\textcolor{red}{f_n(x) = \sin nx / 2^n }$ とする。このとき，

\begin{aligned} \left| \frac{\sin nx }{2^n} \right| \le \frac{1}{2^n}, \quad x \in \mathbb{R} \end{aligned}

かつ $\sum_{n=1}^\infty 1/2^n = 1 < \infty$ より，ワイエルシュトラスのM判定法から，

\textcolor{red}{\sum_{n=1}^\infty \frac{\sin nx}{2^n}}

は $\mathbb{R}$ 上絶対一様収束（絶対収束かつ一様収束）する

$\mathbb{R}$ 上全体で絶対一様収束するのがわかりますね。

例2.

$\textcolor{red}{f_n(x) = x^n /\log (n+1) }, \,\, 0 < a < 1$ とする。このとき，

\begin{aligned} \left| \frac{x^n }{\log (n+1)} \right| \le \frac{a^n}{\log 2}, \quad x \in [-a, a] \end{aligned}

かつ $\sum_{n=1}^\infty a^n = a/(1-a) < \infty$ より，ワイエルシュトラスのM判定法から，

\textcolor{red}{\sum_{n=1}^\infty \frac{x^n}{\log( n+1)}}

は $[-a, a]$ 上絶対一様収束（絶対収束かつ一様収束）する

$[-a, a]$ 上 $(0 < a < 1)$ であることに注意してください。たとえば， $[-1, 1]$ や $(-1, 1)$ の上では一様収束しません。
ただし， $(-1, 1)$ の上では広義一様収束します。

広義一様収束については，以下の記事を参照してください。