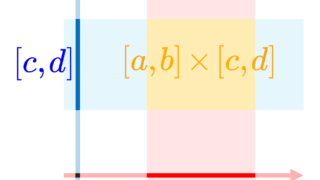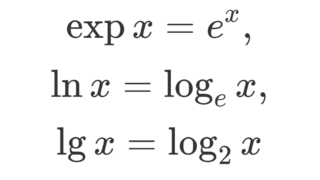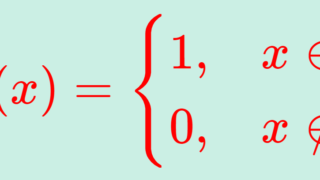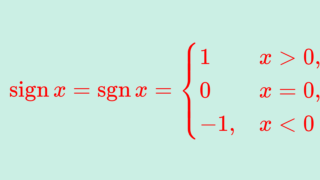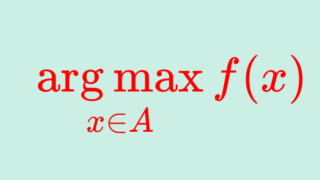ここでは,専門数学において,一般的に使われる記号を一挙に説明しています。高校数学における記号の知識は仮定しますので注意してください。
本サイト (mathlandscape.com) の記号・記法は,全て専門数学で一般的に使われるものとします。本サイトは高校生や数学専攻でない方も対象としていますから,専門数学で使われる用語や記号について説明します。
定義・公理・定理・命題・補題・系
これについては非常に重要ですから,以下の記事を参照してください。
関数・写像
これについても非常に重要ですから,以下の記事を参照してください。
インライン数式
数学においては,式のみで1行を消費する書き方(ディスプレイ形式)と,文中に式を挿入する書き方(インライン形式)があります。
たとえば,ディスプレイ形式の場合
\frac{1}{n}, \, \sum_{k=1}^n a_k, \, \lim_{x \to a} f(x)
と中央ぞろえになるものは, インライン形式では, \frac{1}{n}, \, \sum_{k=1}^n a_k, \, \lim_{x \to a} f(x) のように,記号の添え字の位置が変わることがあります。
これらはどちらも同じ意味であることに注意してください。
また,分数を文中に書くときは一般に \frac{1}{n} と書くよりも, 1/n と書く方が好まれる傾向にあります。本サイトでは主に後者を用いますので,これも同じ意味であることに注意してください。
不等号
a \le b と a \leqq b , a \ge b と a \geqq b は同じ意味です。高校では等号が二本ものが良く使われますが,一般には,等号部分が一本の方が良く使われます。本記事では,主に等号が一本のものを使いますが,状況に応じて二本のものも使います。
和の記号・積の記号
\begin{gathered} \sum_{k=1}^n a_k = a_1 + a_2 + \cdots + a_n, \\ \prod_{k=1}^n a_k = a_1 \times a_2 \times \cdots \times a_n \end{gathered}とします。
数の集合・集合の記法
数の集合は以下の記号を使います。
- \mathbb{Z} :整数 (integer) 全体の集合
- \mathbb{Q} :有理数 (rational number) 全体の集合
- \mathbb{R} :実数 (real number) 全体の集合
- \mathbb{C} :複素数 (complex number) 全体の集合
なお, \mathbb{N} はふつう自然数 (natural number) の集合を表しますが,自然数には 0 を含む流儀と含まない流儀があるため,できるだけ使用しないことにします。これに関してはふつうに n \ge 1 や n \ge 0 とかいて伝わる文脈がほとんどだと思うので,そうします。
ただし,伝わらない場合に限り,注釈をつけたうえで \mathbb{Z}_{\ge 1}, \mathbb{Z}_{\ge 0} という風なかき方をするか, \mathbb{N}=\{1,2,3,\dots\} のように,0 を含むか明示してから \mathbb{N} を使うことにします。
また, A\subset B は, A\subseteq B と同じ意味とします。
\{f(x)\mid P(x)\},\quad \{f(x); P(x)\},\quad \{f(x)\colon P(x)\}
は,全て集合の内包的表記を指します。
他に,高校ではほとんど習わないものとして,以下の記号を用います。
- A^c :集合 A の補集合
- \overline{A} :集合 A の補集合(大学では上の方が一般的。この使い方をするときは注釈を入れます。)
- A \setminus{B} :集合 A から B を除いた差集合,すなわち A \cap B^c と同じ意味
- \overline{A} :集合 A の閉包(閉包とは位相空間の概念。)
- \prod_{k=1}^n A_k = A_1 \times A_2 \times \cdots \times A_n = \{ (a_1, a_2, \ldots, a_n) \mid a_k \in A_k \} (直積集合)
- A^n = A \times \cdots \times A ( n 個)
- \bigcap_{k=1}^n A_k = A_1 \cap A_2 \cap \cdots \cap A_n
- \bigcup_{k=1}^n A_k = A_1 \cup A_2 \cup \cdots \cup A_n
- \bigcap_{\lambda\in\Lambda} A_\lambda :全ての \lambda\in\Lambda に対して, x \in A_\lambda となる x の集合
- \bigcup_{\lambda\in\Lambda} A_\lambda :ある \lambda\in\Lambda が存在して, x \in A_\lambda となる x の集合
- 2^X = \{A \mid A\subset X\} : X のべき集合
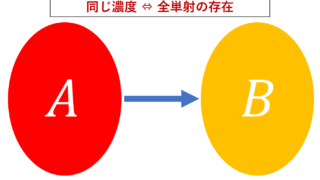
- |A|, \#(A) :集合 A の濃度(有限個のときは要素の個数)
直積集合に関しては,以下で解説しています。
べき集合に関しては以下で解説しています。
集合の濃度については以下で解説しています。
左極限・右極限
\lim_{x \to a-0} f(x), \, \lim_{x \to a-} f(x), \, \lim_{x \uparrow a} f(x)
は全て左極限を表し,
\lim_{x \to a+0} f(x), \, \lim_{x \to a+}f(x), \, \lim_{x \downarrow a} f(x)
は全て右極限を表します。
指数・対数
\exp(x) = e^x です。ただし, e はネイピア数とします。
\log x は自然対数 \log_{e} x や常用対数 \log_{10} x を表すことがありますが,本サイトでは, \log_e x を表すことにします。
海外では,自然対数を \operatorname{ln} x とかくこともあります。この辺は,以下の記事で解説しています。
ZFC,とくに選択公理について
本サイトでは,基本的にはZFCを公理として認めることにします。選択公理を使う定理については,注意を促すようにしますが,「選択公理を使った定理を使う」場合については,言及しない可能性があります。
選択公理を言及すべき記事を見つけた場合は,個別にお問い合わせください。
その他
ここからは,少し重要度が下がるものや,特定の分野でよく使うものをざっと紹介します。
定義関数
1_A (x) = \begin{cases} 1&x \in A,\\ 0& x \notin A \end{cases}定義関数については以下の記事も参照してください。
sign(x), sgn(x)
max, min
\max A ( \min A) で集合 A の最大値(最小値)を指します。たとえば, \max\{ 1,2,3\} = 3 です。集合の内包的表記 \max\{ f(x)\mid P(x)\} を使うときは,代わりに
\max_{P(x)} f(x)
とかくことがあります。たとえば, \max_{1\le x\le 2} x^2 =4 です。
argmax, argmin
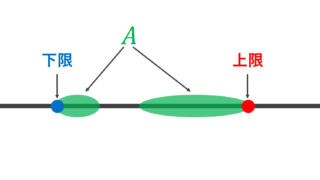
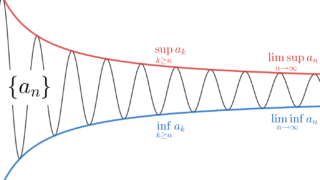
sup, inf
limsup, liminf
見つからない場合は
本ページでは,さまざまな数学の分野で使われる,比較的汎用的な記号のみ記述しています。そうでない記号については,各記事内で解説している場合があります。
以下の全記事一覧では,下に行くほど前提知識が増えるようにまとめてあるため,わからない記号に遭遇した場合,その記事より上の記事を参照すれば,見つかる可能性があります。
また,「記号・用語の定義」タグをみると,早く見つかるかもしれません。
あるいは,検索部分から検索してみてください。