【直積集合】集合の直積について詳しく～具体例10個～

集合 $A,B$ に対し，その直積 $A\times B$ は， $a\in A,\; b\in B$ の対(順序対) $(a,b)$ の集合となります。

そんな直積について，2個の直積・n個の直積・無限個の直積を，具体例を添えながら，順番に解説していきましょう。

2つの集合の直積
1. 2つの集合の直積とは
2. 2つの集合の直積の具体例
n個の集合の直積
無限個の集合の直積
1. 無限個の集合の直積とは
2. 無限個の集合の直積の具体例

2つの集合の直積

2つの集合の直積とは

定義（2つの集合の直積）

集合 $A,B$ に対して，その2つの要素 $a\in A,\; b\in B$ を対にした $(a,b)$ の集合

\color{red}A\times B = \{(a,b)\mid a\in A, \; b\in B\}

を $A$ と $B$ の直積 (direct product) またはデカルト積 (Cartesian product) という。同じ集合の直積 $A\times A$ は $\color{red} A^2$ とも表す。

ここで， $(a,b)$ を順序対（じゅんじょつい; orderd pair）といいます。順序対は順序を考慮し，一般に $(a,b)\ne (b,a)$ です。順序対の集合を直積というわけですね。

また，順序対は順序を考慮するわけですから，一般に $A, B$ が空でないとき， $A\ne B$ なら $A\times B\ne B\times A$ も成り立ちます。

早速，具体例をみましょう。

2つの集合の直積の具体例

例1.

$A=\{a,b,c\}, \; B=\{1,2\}$ とすると，

\small A\times B=\{ (a,1),(a,2),(b,1),(b,2),(c,1),(c,2)\} .

下のような表を考えると分かりやすいでしょう。

	$a$	$b$	$c$
$1$	$\color{red} (a,1)$	$\color{red}(b,1)$	$\color{red} (c,1)$
$2$	$\color{red} (a,2)$	$\color{red} (b,2)$	$\color{red}(c,2)$

このように，集合 $A,B$ の要素の個数(濃度)を $|A|,|B|$ と表すことにすると， $A\times B$ の要素の個数は $|A\times B| = |A|\times |B|$ になります。

例2.

$A=\{a,b\}$ とすると，

A^2 = \{ (a,a), (a,b), (b,a), (b,b) \}.

これも，下の表を考えるとよいです。

	$a$	$b$
$a$	$\color{red} (a,a)$	$\color{red}(b,a)$
$b$	$\color{red} (a,b)$	$\color{red} (b,b)$

例3.

実数全体の集合 $\mathbb{R}$ に対して，

\mathbb{R}^2=\{ (x,y)\mid x\in \mathbb{R}, \; y\in \mathbb{R}\}

は，座標平面上の全ての点の集合を指す。

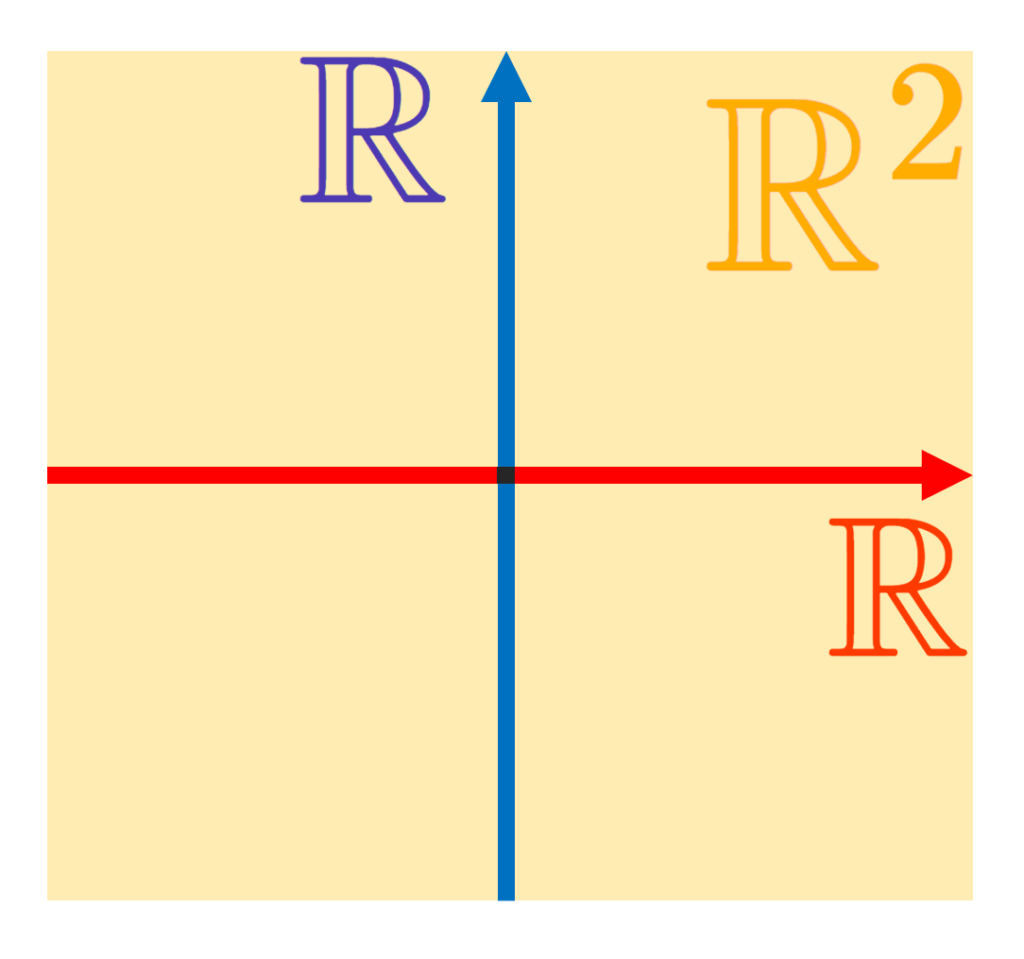
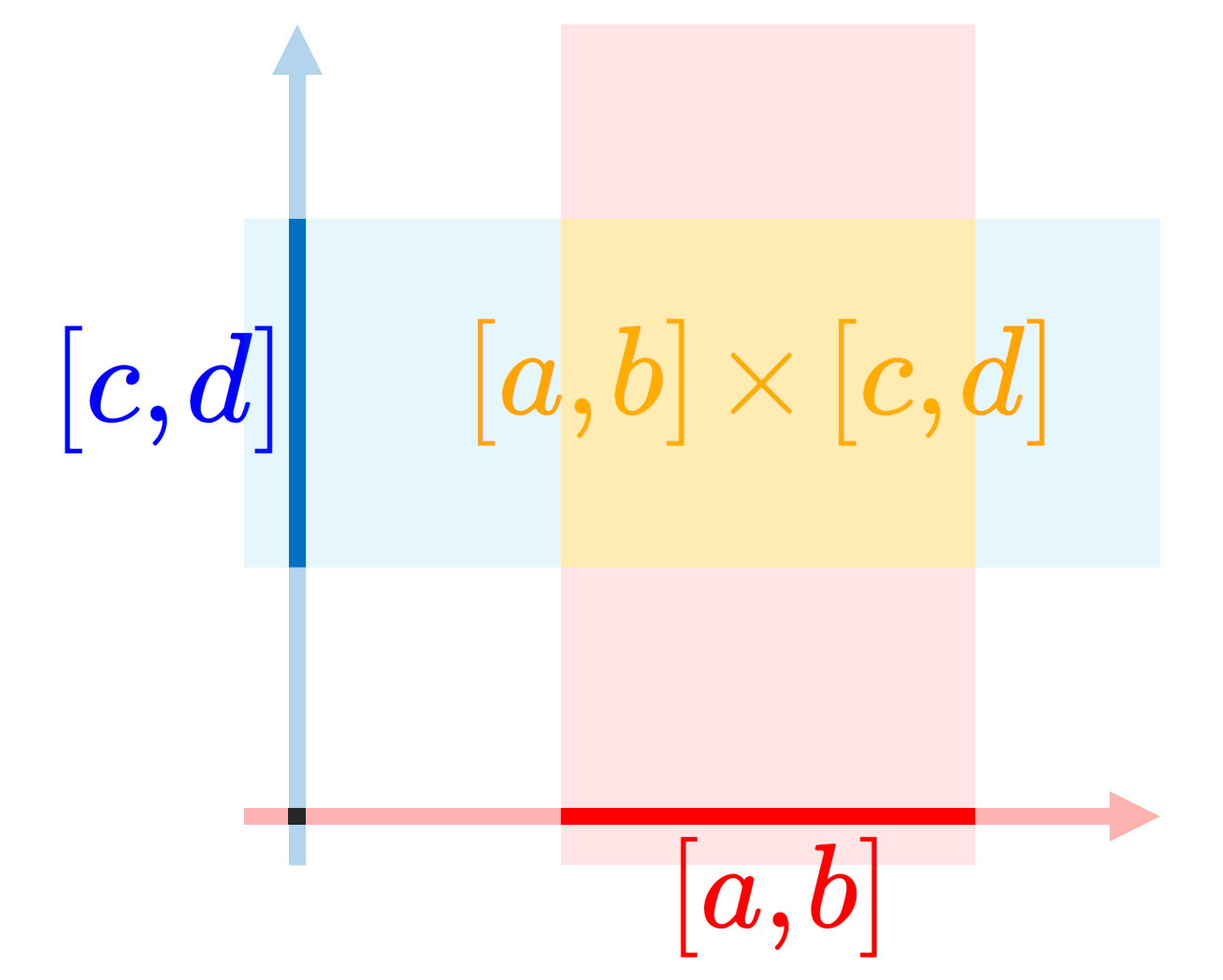
また，他にも例えば区間の直積 $[a,b] \times [c,d]$ は以下の黄色い部分の点の集合を指します。

最後に，以下の例も注意しておきましょう。

例4.

$A,B$ のうち，少なくとも片方が空集合のときは $A\times B =\emptyset$ である。

一つでも空集合があると，順序対が作れなくなってしまうので，直積は空集合になります。

n個の集合の直積

2つの順序対の集合を考えたのが $2$ つの直積でした。これを， $n$ 個の順序対の集合にしたものが， $n$ 個の直積です。

n個の集合の直積とは

定義（ $n$ 個の集合の直積）

集合 $A_1, A_2, \dots, A_n$ に対して，

\color{red}\begin{aligned} &A_1\times A_2\times \dots \times A_n \\ &=\{ (a_1,a_2,\dots,a_n)\mid a_k\in A_k\; (1\le k\le n)\}\end{aligned}

を $A_1,A_2,\dots, A_n$ の直積 (direct product) またはデカルト積 (Cartesian product) という。これを， $\displaystyle \color{red}\prod_{k=1}^n A_k$ とかくこともある。

同じ集合 $A$ の $n$ 個の直積は $\color{red} A^n$ とも表す。

$2$ 個が理解できれば， $n$ 個の直積も比較的容易に理解できるのではないでしょうか。

n個の集合の直積の具体例

例5.

$A=\{1,2\},\; B=\{a,b\} , \;C=\{ \alpha, \beta\}$ とすると，

\begin{aligned}&A\times B\times C \\&= \{ (1,a,\alpha),(1,a,\beta), (1,b,\alpha), (1,b,\beta),\\ & \qquad (2,a,\alpha),(2,a,\beta), (2,b,\alpha), (2,b,\beta) \} .\end{aligned}

例6.

実数全体の集合 $\mathbb{R}$ に対して，

\mathbb{R}^3=\{ (x,y,z)\mid x,y,z\in \mathbb{R}\}

は，座標空間上の全ての点の集合を指す。

一般に，集合 $A$ の要素の個数(濃度)を $|A|$ と表すことにすると， $|A_1\times \dots \times A_n| = |A_1|\times \dots \times|A_n|$ になります。

$A_1, \dots, A_n$ のうち，少なくとも一つが空集合のときは，その直積も空集合です。

直積集合と写像

ここからは少しレベルを上げて，直積集合と写像の関係について述べます。無限個の集合の直積を定義するにあたっては，この理解はほぼ必須です。逆に言えば，無限個の直積を知る必要がないのであれば，ここで引き返しても構いません。

さて，

(a_1, a_2, \dots, a_n)\in A_1\times A_2\times \dots \times A_n

とはどういう意味でしょうか。これは，各 $1\le k\le n$ に対して， $a_k\in A_k$ ですから，これは，各集合 $A_k$ から一つずつ要素を選び，順番に並べたものと言えますね。

これをさらに言い換えると，これは，各集合の添え字 $1\le k\le n$ に対して， $a_k \in A_k$ を対応させているといえます。この対応は「写像」といえますね。

すなわち， $(a_1, a_2, \dots, a_n)$ は， $f(k) = a_k$ となる写像 $f$ に対応している(同一視ができる)わけです。直積集合は，そのような写像全体の集合と考えることができるため，以下のように書くことができます。

A_1\times\dots \times A_n = \{ f\mid f(k) \in A_k \; (1\le k\le n) \}.

ここで， $f$ は $\color{red} f\colon \{1,2,\dots, n\} \to \bigcup_{k=1}^n A_k$ と考えるとよいです。このような定義域・終域を持つ写像のうち， $f(k)\in A_k$ をみたすもの全体が，直積集合に対応しているわけです。
改めてちゃんと書くと，以下のようになります。

命題（直積集合と写像）

$A_k \; (1\le k \le n)$ を集合とする。このとき，

\color{red} \prod_{k=1}^n\! A_k\! = \!\left\{\! f\colon \! \{1,\dots, n\} \to \bigcup_{k=1}^n\! A_k \middle|\begin{aligned} &f(k) \in A_k \\ &{\small (1\le k\le n)}\end{aligned} \!\right\}

である。

「命題」としましたが，むしろ「順序対」なしで直積集合を定義しようと思うと，これを定義にした方が良いかもしれません。この発想を用いて，無限個の直積集合を定義しましょう。

無限個の集合の直積

無限個の直積集合は，ラフに言うと無限個の順序対 $(a_1,a_2,\dots)$ と思うかもしれません。無限個の直積を考える機会が少ないのであれば，取り敢えずその理解でも良いでしょう。

ただし，実際はそれではいけません。無限と言っても非可算無限のこともあるので， $(a_1,a_2,\dots)$ と思うのは少し無理があります。先ほどの写像の議論を用いて，厳密に定義しましょう。

可算無限・非可算無限については，以下で解説しています。本記事では，以下が分からなくても，読むことが可能です。

既に確認したとおり，以下の定義は有限個の場合でも通用します。

無限個の集合の直積とは

定義（無限個の直積）

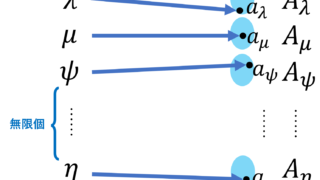
集合 $\Lambda$ を添え字とする集合族 $\{ A_{\lambda}\}_{\lambda\in\Lambda}$ に対し，

\color{red} \prod_{\lambda\in\Lambda}\! A_{\lambda}\! = \!\Bigl\{\! f\colon \! \Lambda \to \bigcup_{\lambda\in\Lambda} \! A_\lambda \Bigm|f(\lambda) \in A_\lambda \;(\lambda\in\Lambda) \!\Bigr\}

を $\{ A_{\lambda}\}_{\lambda\in\Lambda}$ の直積 (direct product) またはデカルト積 (Cartesian product) という。同じ集合の直積 $\prod_{\lambda\in\Lambda} A$ は $\color{red} A^{\Lambda}$ とも表す。

先ほどの $n$ 個の直積でやった写像の議論を，無限も許す場合に拡張していますね。ここでいう無限は，可算無限とは限らず，非可算無限でも構いません。

例を挙げておきましょう。

無限個の集合の直積の具体例

例7.

$\prod_{x\in \mathbb{R}} \{x\}$ の元は， $f(x)=x$ となる $f\colon \mathbb{R}\to \mathbb{R}$ のみである。

例8.

$\mathbb{N}=\{1,2,3,\dots \}$ とする。

$\prod_{n\in\mathbb{N}} [n, n+1]$ の元は， $n\le f(n)\le n+1$ となる $f\colon \mathbb{N}\to [1,\infty)$ である。特にこれは， $n\le a_n\le n+1$ となる数列 $\{a_n\}_{n=1}^\infty$ と思える。すなわち，

\begin{aligned}&\prod_{n\in\mathbb{N}} [n, n+1]\\ &= \{ \{a_n\}\mid n\le a_n\le n+1\; (n\ge 1) \}\end{aligned}

である。

このように，添え字集合が $\mathbb{N}$ であれば，無限個の順序対 $(a_1,a_2, \dots )$ と捉えることが可能である「数列」と思えますね。

例9.

定義より，

A^{\Lambda} = \{f\colon \Lambda\to A\}

である。すなわち， $A^{\Lambda}$ は写像 $f\colon \Lambda \to A$ 全体の集合である。

べき集合は $2^A$ とかきますが，これは，べき集合は写像 $f\colon A\to \{0,1\}$ の集合と思えるからです。

例10.

$\{A_\lambda\}_{\lambda\in\Lambda}$ のうち，少なくとも一つが空集合であるとき， $\prod_{\lambda\in \Lambda} A_{\lambda}=\emptyset$ である。

なお，一般に例10の逆「 $A_\lambda \ne \emptyset \;(\lambda\in\Lambda)\implies \prod_{\lambda\in \Lambda} A_{\lambda} \ne \emptyset$ かどうかは自明ではありません。例7,8,9のような場合は空でないことが言えていますが，一般には空かどうかは確認不能であることが知られています。

そこで，これが空でないというのを認めるのが選択公理 (axiom of choice) です。これについては，以下で解説しています。