選択公理の内容と具体例を詳しく

選択公理とは，「無限個の各集合から一気に一つずつ元を選択することができる」という公理です。専門数学では，多くの場合仮定されますが，自明でない公理なので，気を付けて使う必要があります。

そんな選択公理について，その内容と意味・具体例を詳しく解説しましょう。

選択公理とは
選択公理の具体例
1. 選択公理が不要な例
2. 選択公理が必要な例
選択公理から従う奇妙な定理
参考

選択公理とは

まずは「選択公理」とは何か述べ，それからイメージを語ることにしましょう。

選択公理の主張

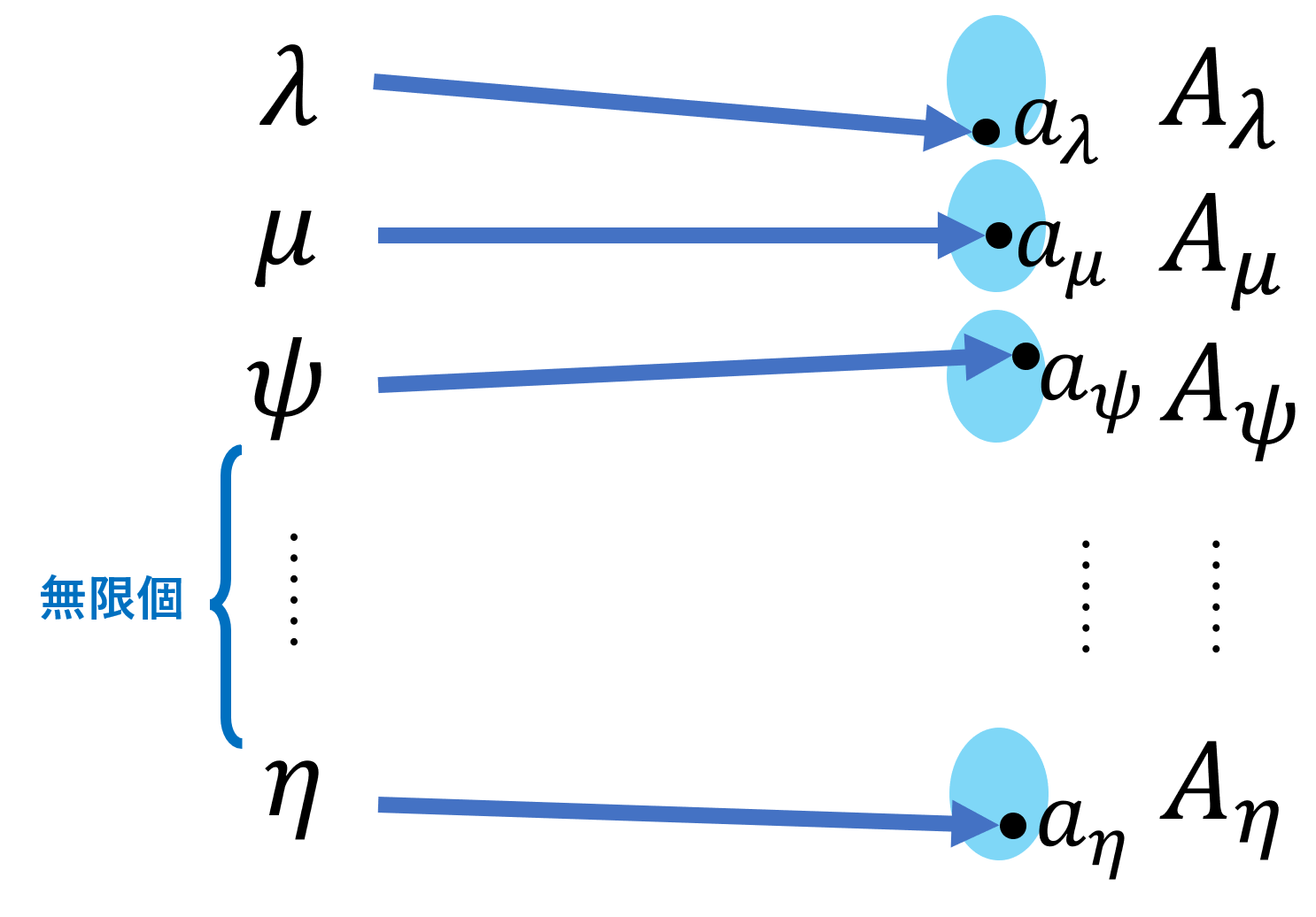
選択公理 (axiom of choice; AC)

$\Lambda$ を無限集合とし， $\Lambda$ の元で添え字付けられた集合族 $\{A_\lambda\}_{\lambda\in\Lambda}$ は，どれも空でないとする。このとき，

\color{red}\large \prod_{\lambda\in\Lambda} A_\lambda \ne \emptyset

である。

ここで，はじめに注意ですが， $\prod_{\lambda\in \Lambda} A_{\lambda} \ne \emptyset$ には，必ずしも選択公理が必要になるわけではありません。選択公理を用いずとも，このことが示せる場合もあります。これについては，後ほどの具体例で詳しく確認していきましょう。

定義が意味不明かもしれませんね。 $\prod_{\lambda\in\Lambda} A_\lambda$ は，無限個の集合の直積を指し，以下のように定義されます。

無限個の直積

\prod_{\lambda\in\Lambda}\! A_{\lambda}\! = \!\Bigl\{\! f\colon \! \Lambda \to \bigcup_{\lambda\in\Lambda} \! A_\lambda \Bigm|f(\lambda) \in A_\lambda \;(\lambda\in\Lambda) \!\Bigr\}

詳しくは以下で解説しています。

これを用いると，選択公理は，この等式の両辺が空でないと言っているわけですから，以下のように書き換えることができます。

選択公理の言い換え

$\Lambda$ を無限集合とし， $\Lambda$ の元で添え字付けられた集合族 $\{A_\lambda\}_{\lambda\in\Lambda}$ は，どれも空でないとする。

このとき，写像 $\color{red} f\colon \Lambda \to \bigcup_{\lambda\in\Lambda} A_{\lambda}$ で， $\color{red} f(\lambda)\in A_\lambda \; (\lambda\in\Lambda)$ をみたすものが存在する。

このときの $f$ を選択関数 (choice function) といいます。写像の言葉でかけましたね。

なお，逆に $\{A_\lambda\}_{\lambda\in\Lambda}$ のうち，一つでも空集合があれば，その直積は空集合になります。実際， $f(\lambda)\in \emptyset$ となるような写像 $f$ があるのは意味不明なので，明らかです。

選択公理のイメージ

選択公理の具体的なイメージを考えましょう。「選択公理」とは，その名の通り，各集合から元を一つずつ「選択」する動作を指しています。集合は無限個ありますから，無限個の各集合から，元を一つずつ「一気に選択」するわけです。

「選択」には自由度がありますから，テキトーに取ってこねばなりません。この「テキトー」を一気に無限回できると言っているのです。

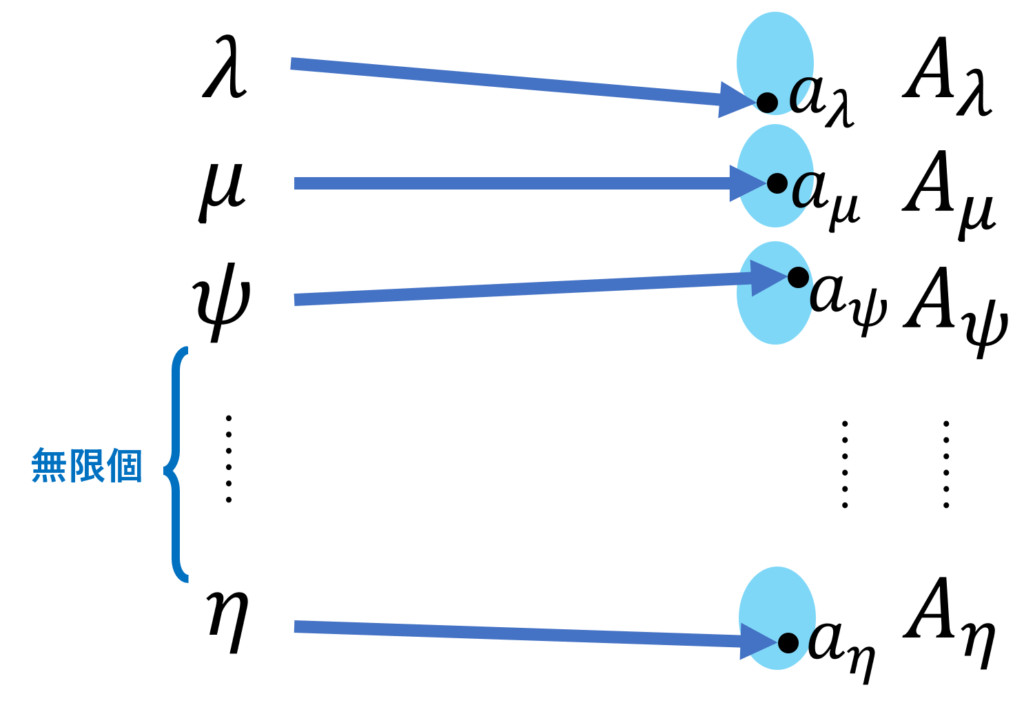
帰納法を用いれば，無限個の選択は容易と思うかもしれませんが，これは誤りです。帰納法は「一気に」無限個を選択しているわけではなく，常に有限個の選択です。そして，この「選択」作業は終わらず，無限個を選択した状況に出くわすことはないのです。

選択公理とZFC公理系

選択公理は，公理的集合論における公理の1つで，ZF公理系と呼ばれる集合の基本公理に加えて，公理とされるものです。ZF公理系と選択公理を合わせてZFC公理系と言います。

ZF公理系は感覚的にも基本的なものですが，選択公理はそうではなく非自明で，仮定するかどうかが論争になることもあります。
実際は，ZF公理系の範疇では，選択公理が正しいかどうかの証明は不可能であることが知られており，選択公理を仮定するかは「自由である」といった具合です。

現実，ZFC公理系は，現代数学の多くの理論で仮定されています。

選択公理の具体例

さて，選択公理の定義を述べました。選択公理とは，厳密に述べると「選択関数が存在すること」で，感覚的に述べると「無限個の集合から一気に無限個の元を取り出してこれる」でした。

選択公理の具体例を考えましょう。

選択公理が不要な例

選択公理が不要な例1.

$A_1, A_2, \dots, A_n$ を空でない集合とするとき，

A_1\times A_2 \times \dots \times A_n \ne \emptyset.

有限個の集合の直積に関しては，選択公理は不要です。選択という動作を有限回するだけであれば，全く問題はないのです。実際，有限個の場合は適当に $a_1\in A_1, \dots, a_n \in A_n$ を「選択」し，その順序対 $(a_1,a_2,\dots, a_n)$ が直積集合の元になります。

実際のところ，有限個の直積が空でないのは，ZF公理系の理解が必須ですが，とにかく可能であると思っておくとよいでしょう。

さて，次からは無限個の直積でも選択公理が不要な例を確認します。

選択公理が不要な例2.

$\Lambda$ を無限集合とする。

\mathbb{Z}^\Lambda=\prod_{\lambda\in\Lambda} \mathbb{Z} \ne \emptyset.

これは例えば，選択関数として $f(\lambda) =0\;(\lambda\in\Lambda)$ とすれば良いだけですから，直積集合は空でありません。

このように，具体的に選択関数を一つ取ってこれる場合は，選択公理は不要です。

選択公理が不要な例3.

$\Lambda\subset \mathbb{R}$ とする。このとき，

\prod_{\lambda\in \Lambda} [\lambda, \lambda+1] \ne \emptyset.

これも，選択公理は不要です。実際， $f(\lambda)=\lambda$ とすれば， $f\colon \Lambda\to \bigcup_{\lambda\in\Lambda} [\lambda, \lambda+1]$ は選択関数の1つですね。

このように，各集合に具体的な性質が備わっている場合は，選択関数を実際にかける場合が多く，選択公理は不要です。

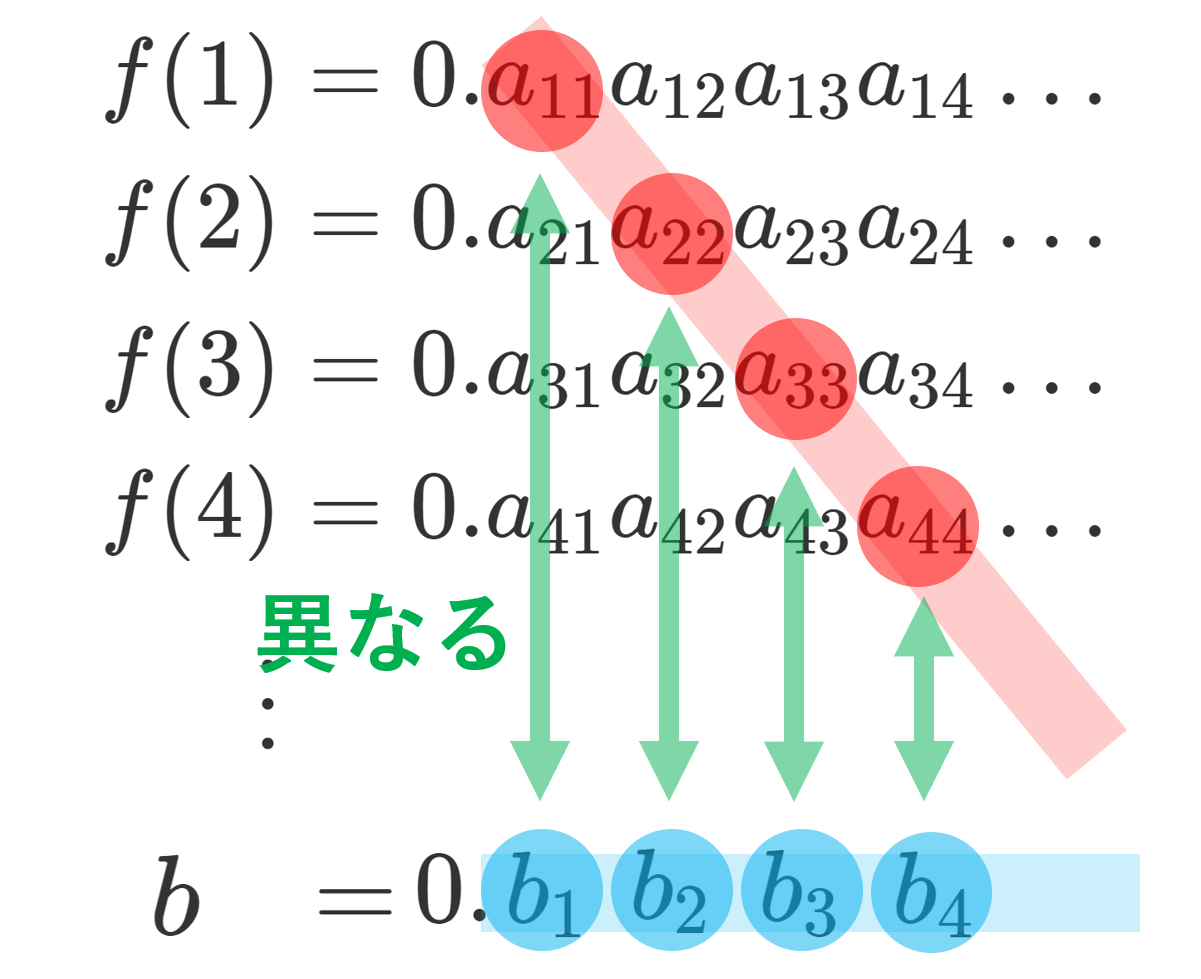
他にも，たとえば $|\mathbb{N}|<|\mathbb{R}|$ を示す対角線論法では，選択公理は不要です(→カントールの対角線論法とそれを用いた証明)。

選択公理が必要な例

選択公理が必要な定理のうち，代表的なものを2つ紹介しましょう。

「可算集合」の定義の知識を仮定しますが，簡単に言うと可算集合とは，要素に正の整数で番号付けられる集合，すなわち正の整数の集合と全単射が作れる集合を指します(→可算集合と非可算集合(可算無限・非可算無限))

1. 有限集合の非交和は可算集合

選択公理が必要な定理1.

集合族 $\{A_n\}$ は互いに素かつ $|A_n| = 2$ (集合の個数) をみたすとする。このとき， $\bigcup_{n=1}^\infty A_n$ は可算集合である。

どこで選択公理を使っているか考えながら，証明を確認しましょう。

証明

各 $A_n$ の元を $a_{n,1},a_{n,2}$ と番号付けする。すると， $\{a_{n,k}\}_{n,k}$ の濃度は $|\mathbb{N}\times 2|$ であり， $|\mathbb{N}\times 2| = |\mathbb{N}|$ なので，可算集合である。

証明終

各集合の元を番号付けしていますが，各 $A_n$ について，この番号付けの仕方は $2$ 通りあり，そこから一方を「選択」せねばなりません。この $2$ 通りの集合を $F_n$ とすると， $\prod_{n=1}^\infty F_n$ が空でないことを用いています。

同じく，選択公理を認めれば，集合族 $A_n$ が高々可算集合のとき， $\bigcup_{n=1}^\infty A_n$ が高々可算集合であることも示せます。証明は可算集合と非可算集合(可算無限・非可算無限)で行っています。

注意ですが，たとえば $A_n \subset\mathbb{R}$ であれば，小さい元から順に $a_{n,1}<a_{n,2}$ と「具体的」に番号付け可能なので，選択公理は不要です。このときの選択関数は， $f(n,1)=\min A_n,\; f(n,2) = \max A_n$ とすると，写像 $f(n,\cdot)\colon \{1,2\}\to A_n$ は番号付けのルールを表し，

(f(n, \cdot))_n \in \prod_{n=1}^\infty F_n

と，具体的に取ることができました。具体的な構造があれば，選択公理は不要になります。

2. 無限集合は必ず可算集合を含む

選択公理が必要な定理2.

無限集合は必ず可算部分集合を含む。

これはすなわち，無限の濃度で最小のものが可算濃度であることを意味します。

証明

$A$ を無限集合とする。 $a_1\in A$ を一つ「選択」する。続いて， $a_2\in A\setminus\{a_1\}$ を一つ「選択」する。続いて， $a_3\in A\setminus\{a_1,a_2\}$ を一つ「選択」する。

同様の操作を「無限回」繰り返すことで可算集合 $\{a_n\}\subset A$ を得る。

証明終

「無限個の選択」をしていますね。これは，選択公理により，

f\in\prod_{C\subset A} C = \prod_{C\in 2^A} C

が取れて，これを用いて，帰納的に $a_1=f(A), \; a_2=f(A\setminus\{a_1\}),\; a_3=f(A\setminus\{a_1,a_2\}),\dots$ としていけばよいです。帰納法の部分では，もう「選択」していませんね。

その他の例

その他，選択公理が必要な有名な例を述べましょう。

選択公理が必要な例

特に，上4つは選択公理と同値です。

なお，選択公理をひとたび認めると，直積集合の元の個数は各集合以上であることが容易にわかります。すなわち， $\left| \prod_{\lambda\in \Lambda} A_\lambda\right|\ge |A_\lambda|$ です。

実際， $f \in \prod_{\lambda\in \Lambda} A_\lambda$ を選択関数とすると，各 $a\in A_\lambda$ に対し，これを選択する選択関数

g(x) =\begin{cases}a & x=\lambda, \\ f(x) & x\ne \lambda\end{cases}

も選択関数になるからです。

選択公理から従う奇妙な定理

選択公理は，多くの数学において仮定されることが多いですが，これを仮定すると，以下のような奇妙な定理が示せることが知られています。

定理（バナッハ－タルスキー）

選択公理を仮定する。

このとき，3次元球を有限個の部分に分割し，それらを回転・平行移動のみを用いて組み替えることで，同じ大きさの球を2つ作ることができる。

これは要するに，「分解してもう一回組めば体積が変わる」と言っています。不思議な定理ですね。

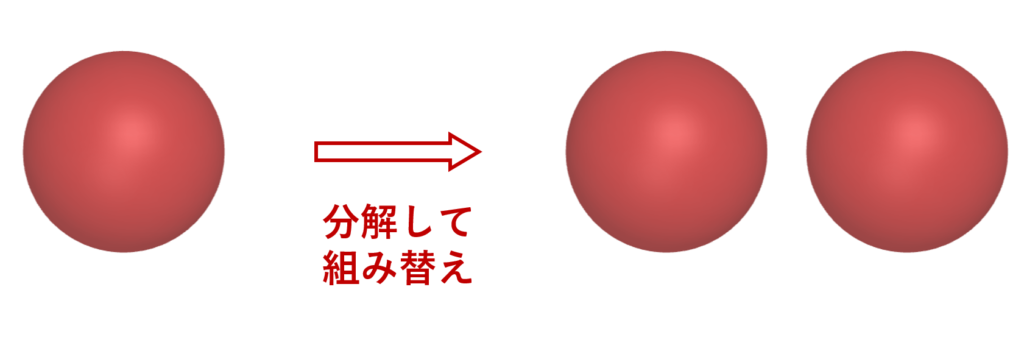
このような定理からも，選択公理は自明なものではなく，非常に奇妙な公理である，といえます。

この定理は非常に奇妙ですから，やはり選択公理は仮定すべきでないのでしょうか。難しい問題ですね。