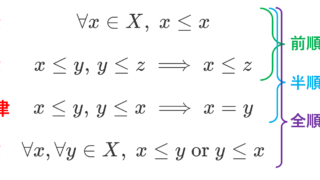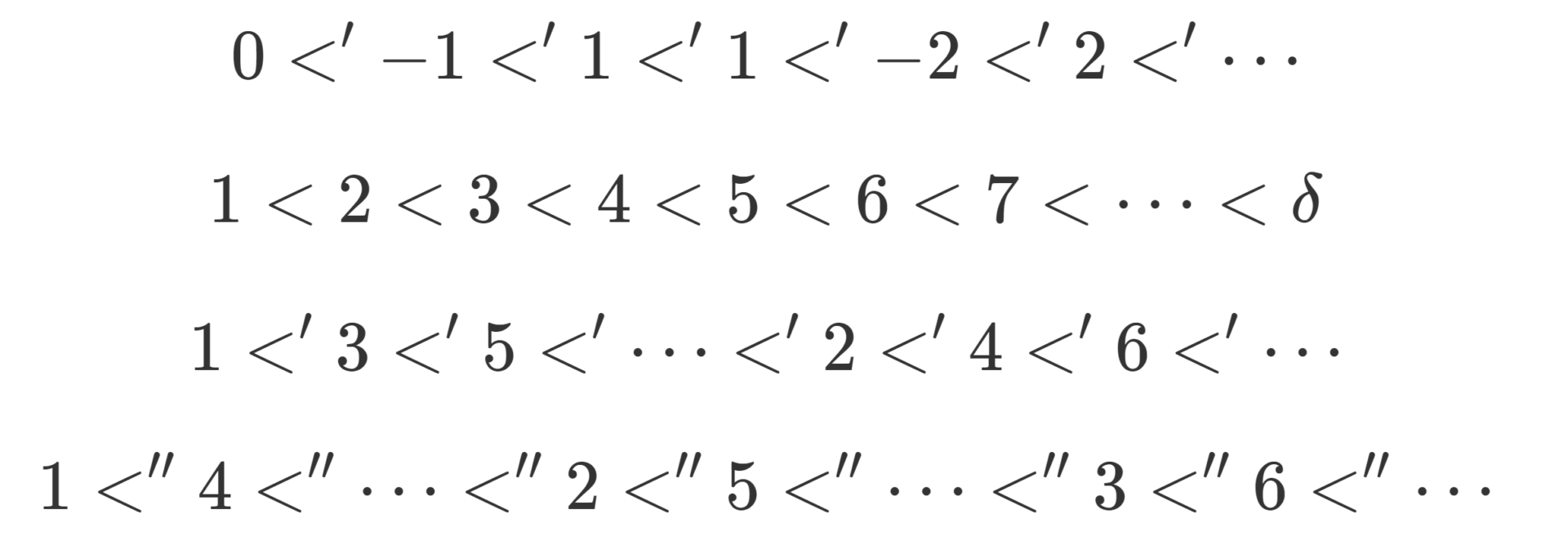ツォルンの補題とその証明のスケッチ・応用例

ツォルンの補題は，補題と言われていますが数学における大事な定理の1つで，選択公理と同値です。ツォルンの補題について，その主張と証明のスケッチを紹介し，さらにツォルンの補題を用いて証明される定理について述べましょう。

ツォルンの補題とその証明のスケッチ
ツォルンの補題を用いた証明の例
関連する記事
参考

ツォルンの補題とその証明のスケッチ

ツォルンの補題の主張を理解するためには，まずいくつかの準備が必要です。

準備～帰納的半順序集合と極大元～

以下で，半順序集合・全順序集合の理解は前提とします。これについては，半順序集合・全順序集合の定義・具体例4つとその周辺を確認してください。

定義（帰納的半順序集合・極大元）

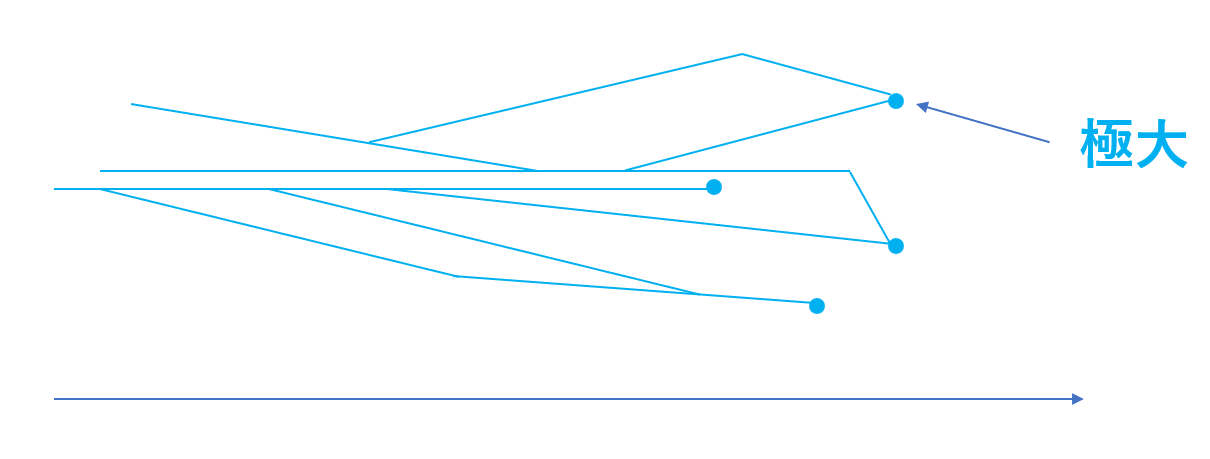
$X$ が帰納的 (inductive) であるとは，任意の全順序部分集合 $A$ が上界を持つことを言う。ただし， $u\in X$ が $A$ の上界 (upper bound) であるとは， $a\le u\; (a\in A)$ が成り立つことを言う( $u\in A$ か否かはどっちでもよい)。

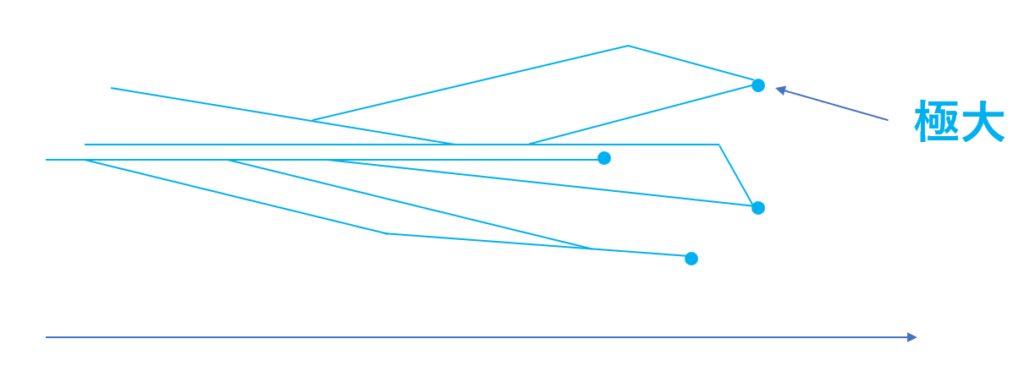
$a\in X$ が $X$ の極大元 (maximal element) であるとは， $a<x$ となる $x\in X$ が存在しないことを言う。すなわち，任意の $x\in X$ に対し， $x\le a$ または $a$ と $x$ の大小が定まらない。

たとえば， $X=[0,1]$ のとき， $1$ がどの集合の上界にもなるため，これは帰納的です。一方で， $X=[0,1)$ のとき， $X$ 自身に上界がありませんから，帰納的ではありません。

これを基に，ツォルンの補題の主張を確認しましょう。

ツォルンの補題の主張

ツォルンの補題 (Zorn’s lemma)

帰納的半順序集合 $X$ は少なくとも一つの極大元をもつ。

言い換えると，任意の全順序部分集合が上界を持つような半順序集合は少なくとも一つの極大元をもつといえます。

ツォルンの補題は選択公理と同値(ZF公理系において)です。選択公理と同値な命題として，他にも整列可能定理が有名です。

本サイトでは，選択公理を用いてツォルンの補題の証明のスケッチを述べ，ツォルンの補題を用いて整列可能定理のスケッチを述べ，整列可能定理を用いて選択公理を証明することで，同値性を担保しています。本ページでは赤字のみ行い，緑字については整列集合と整列可能定理で紹介しています。

ツォルンの補題の証明のスケッチ

証明すると長くなるため，概略を述べるにとどめます。文献[1]を参考にしています。証明には，整列集合に関する知識を使います。確認しておきましょう。

整列集合

全順序集合のうち，任意の空でない部分集合が最小元をもつものを整列集合 (well-ordered set) という。整列集合 $W$ と $a\in W$ に対し，

\color{red} W\langle a\rangle =\{x\in W\mid x<a\}

を $W$ の $a$ における切片 (section) という。切片もまた整列集合である。

整列集合とその切片の性質について詳しくは整列集合と整列可能定理で解説しています。

以下で，整列部分集合 $W\subset X$ と $a\in W$ に対し，切片 $W\langle a\rangle$ における上界を

W^{\uparrow}[a]=\{ x\in X\mid \forall w\in W\langle a\rangle , \, w<x\}

とします。定義から明らかに $a\in W^{\uparrow}[a]$ ですし， $m=\min W$ とすると， $W\langle m\rangle =\emptyset$ なので， $W^{\uparrow}[m]=X$ です。

証明のスケッチ

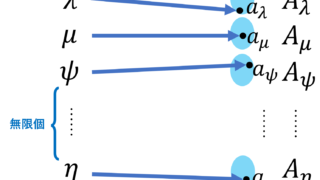
選択公理により，帰納的半順序集合 $X$ 上に選択関数 $f\colon 2^X\to X$ を定める(ただし， $2^X$ はべき集合)。
全ての $a\in W$ に対して， $f(W^{\uparrow}[a])=a$ が成り立つような整列部分集合 $W\subset X$ 全体の集合を $\mathscr{W}$ とする。 $a_1=f(X)$ に対して $\{a_1\}\in \mathscr{W}$ より， $\mathscr{W}\ne \emptyset$ である。
W_{\infty} =\bigcup_{W\in \mathscr{W}} W とすると， W_\infty\in \mathscr{W} である。実際，以下が示せる。
1. $W_\infty$ は整列集合であり，任意の $W\in \mathscr{W}$ に対し， $W=W_{\infty}$ または $W=W_\infty\langle w\rangle$ となる $w\in W_\infty$ が存在する。
2. 上より， $a\in W_{\infty}$ に対し， $a\in W$ となる $W\in \mathscr{W}$ を取ると， $W^{\uparrow}_\infty[a]=W^{\uparrow}[a]$ である。ゆえに， $f(W^{\uparrow}_\infty[a])=f(W^{\uparrow}[a])=a$ となって， $W_\infty \in \mathscr{W}$ がいえる。
$X$ は帰納的であるから， $W_\infty$ には上界 $u\in X$ が存在する。 $u$ が $X$ の極大元の一つになっていることが示せれば証明が終わる。もしそうでないと仮定すると，
$W^\uparrow=\{ x\in X\mid \forall w\in W,\, w<x\}\ne \emptyset$
である。 $u'=f(W^{\uparrow})\in W^\uparrow$ とすると， $W_*=W_\infty\cup \{ u'\}$ も整列集合で， $W_*\in \mathscr{W}$ となるが，これは $W_\infty$ の定義に矛盾している。よって示せた。

証明のスケッチ終

長くなるのは項目3.1.の証明で，整列集合の性質の部分です。逆にこれを認めると，上のように簡単な証明になります。項目3.1.の証明には，おおよそ以下の手順を辿ります。

$W_1, W_2\in\mathscr{W},\, W_1\ne W_2$ とすると，一方は片方の切片に一致していることを示す。整列集合の比較定理より，一方は片方の切片に「順序同型」であることはよい。 $\varphi\colon W_1\simeq W_2\langle a\rangle$ とし，
$x_0=\min \{x\in W_1\mid \varphi(x)\ne x\}$
とする(背理法で右辺が空でないと仮定)と，
$x_0=f(W_1^{\uparrow}[x_0])=f(W_2^{\uparrow}[\varphi(x_0)])=\varphi(x_0)$
となって矛盾する。
$W_\infty$ が整列集合であることは， $M\subset W_\infty$ に対して， $W\cap M\ne \emptyset$ となる $W\in\mathscr{W}$ を一つ取ると， $\min M = \min W\cap M$ となることからわかる(右辺の存在は $W$ が整列集合であることから来る)。この等式は背理法と1.から証明できる。
$W\in \mathscr{W}$ が $W_\infty\ne W$ となるとき， $w=\min W_\infty \setminus W$ とすることで， $W=W_\infty\langle w\rangle$ が1,2.から示せる。